Основная образовательная программа cb. 5005. 2016 Прикладная математика, фундаментальная информатика и программирование
 Скачать 0.51 Mb. Скачать 0.51 Mb.
|
|
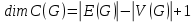 | (1.1) |
2.
 -разрезы формируют базис пространства разрезов
-разрезы формируют базис пространства разрезов  и
и 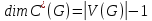 | (1.2) |
3.
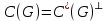 .
. 4.
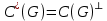 .
.Доказательство.
1. Каждое из ребер
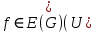 входит в один из
входит в один из 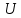 -циклов
-циклов 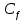 . Следовательно, множество
. Следовательно, множество 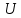 -циклов линейно независимы в
-циклов линейно независимы в 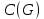 . Далее, для любого элемента
. Далее, для любого элемента 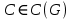 , пусть
, пусть 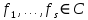 — каждое ребро из
— каждое ребро из 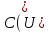 . Тогда элемент
. Тогда элемент 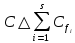 принадлежит
принадлежит 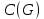 , а его ребра есть ребра дерева
, а его ребра есть ребра дерева 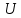 . Следовательно этот элемент равен
. Следовательно этот элемент равен 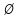 , поэтому
, поэтому 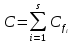 . Откуда можно сделать вывод, что
. Откуда можно сделать вывод, что 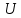 -циклы формируют базис
-циклы формируют базис 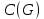 , а размерность
, а размерность 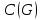 есть
есть 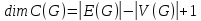 .
.2. Каждое из ребер
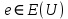 входит в один из
входит в один из 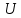 -разрезов
-разрезов 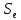 . Следовательно, множество
. Следовательно, множество 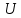 -разрезов линейно независимы в
-разрезов линейно независимы в 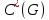 . Пусть
. Пусть 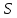 любой элемент
любой элемент 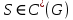 и
и 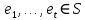 — все ребра из
— все ребра из 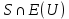 . При чем элемент
. При чем элемент 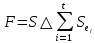 принадлежит
принадлежит 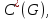 и ни одно из его ребер не является ребром дерева
и ни одно из его ребер не является ребром дерева 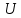 . Если
. Если 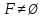 , то, как следует из леммы 1.2 —
, то, как следует из леммы 1.2 — 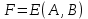 — разрез графа
— разрез графа  . Так как граф
. Так как граф  связный, то, как минимум одно ребро остовного дерева
связный, то, как минимум одно ребро остовного дерева 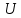 соединяет
соединяет 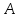 c
c 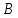 , откуда получаем противоречие. Следовательно,
, откуда получаем противоречие. Следовательно, 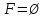 , поэтому
, поэтому 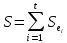 . А последнее означает, что
. А последнее означает, что 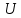 -разрезы образуют базис
-разрезы образуют базис 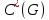 , причем
, причем 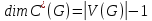 .
.3. Пусть
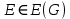 . Из третьего пункта леммы 1.2 получаем, что
. Из третьего пункта леммы 1.2 получаем, что 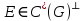 лишь тогда, когда
лишь тогда, когда 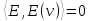 для любого узла
для любого узла 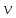 , а именно то, что степень любого узла графа
, а именно то, что степень любого узла графа 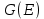 четна. А по лемме 1.1 это означает, что
четна. А по лемме 1.1 это означает, что 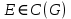 .
.4. Каждый цикл
 пересекает разрез
пересекает разрез 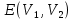 только четное число раз, так как покинув
только четное число раз, так как покинув 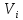 , цикл должен вновь попасть в
, цикл должен вновь попасть в 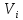 . Следовательно,
. Следовательно, 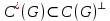 .
.Пусть
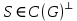 , и
, и 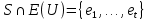 . Как доказано выше, все
. Как доказано выше, все 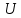 -разрезы
-разрезы 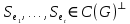 . Тогда и
. Тогда и 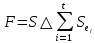 принадлежит
принадлежит 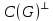 . По построению,
. По построению, 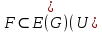 . Если
. Если 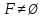 , то рассматривая ребро
, то рассматривая ребро 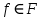 и
и 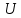 -цикл
-цикл 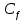 . Получаем, что
. Получаем, что 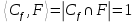 , противоречие. Поэтому
, противоречие. Поэтому 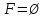 , и, следовательно, что
, и, следовательно, что 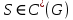 . ∎
. ∎2. ПРАКТИЧЕСКАЯ ЧАСТЬ
2.1 Описание метода с применением теории
В общем случае поиск гамильтонова цикла, к примеру и для всегда гамильтоновых, планарных графов с максимальной степенью узлов три, остается NP-полной задачей со сложностью
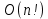 , то есть равен множеству всех перестановок от 1 до n, где n — количество узлов графа
, то есть равен множеству всех перестановок от 1 до n, где n — количество узлов графа  . Один из первых точных алгоритмов перебора — алгоритм Мартелло. Для уменьшения сложности до
. Один из первых точных алгоритмов перебора — алгоритм Мартелло. Для уменьшения сложности до 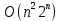 могут быть использованы методы динамического программирования, которые, как видно из оценки сложности алгоритма, также зависят лишь от количества узлов в графе.
могут быть использованы методы динамического программирования, которые, как видно из оценки сложности алгоритма, также зависят лишь от количества узлов в графе.Поставим задачу описать такой алгоритм по нахождению цикла Гамильтона, сложность которого варьируется от количества ребер на графе
 . И для разряженный графов, на которых выполняется неравенство
. И для разряженный графов, на которых выполняется неравенство 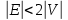 , он имел сложность
, он имел сложность 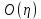 меньшую чем
меньшую чем 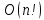 ; выведем
; выведем 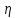 .
.Рассмотрим граф
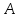 , изображенный на рисунке 2.1, определим его свойства.
, изображенный на рисунке 2.1, определим его свойства.
Рисунок 2.1 - Граф
Граф односвязный, неориентированный, не имеет петель или кратных ребер, количество узлов в графе
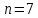 , ребер
, ребер 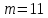 . Матрица инцидентности графа А изображена на таблице 1.
. Матрица инцидентности графа А изображена на таблице 1.Таблица 1 Матрица инцидентности графа А
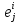 | 1: | 2: | 3: | 4: | 5: | 6: | 7: | 8: | 9: | 10: | 11: |
| 1: | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2: | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| 3: | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| 4: | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| 5: | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | 0 |
| 6: | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 1 |
| 7: | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 |
Итак, по определению на графе задано его циклическое пространство
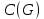 над полем
над полем 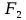 , порождаемое реберным множеством простых циклов, необходимо его найти. Представим матрицу инцидентности как линейную систему над полем
, порождаемое реберным множеством простых циклов, необходимо его найти. Представим матрицу инцидентности как линейную систему над полем 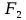 , сложение в которой будет задано согласно определению реберного пространства графа, а именно — сумма элементов определяется как поразрядное сложение по модулю
, сложение в которой будет задано согласно определению реберного пространства графа, а именно — сумма элементов определяется как поразрядное сложение по модулю 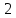 . Эта система есть:
. Эта система есть: 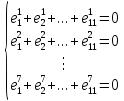 | (2.1) |
Получим решение системы (2.1) с помощью метода Гаусса:
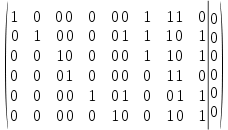 | (2.2) |
При перестановке столбцов
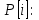
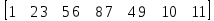
Выразим простые циклы матрицы (2.2) через зависимость базисного минора размерности
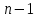 , от
, от 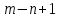 независимых переменных, получим
независимых переменных, получим 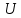 -циклы, изображенные на рисунке 2.2, следующего вида:
-циклы, изображенные на рисунке 2.2, следующего вида: 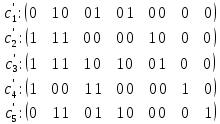 | (2.3) |
где
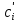 ,
, 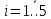 —
— 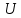 -циклы над полем
-циклы над полем  ,
, 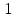 в
в 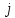 -м столбце соответствует принадлежности соответствующего ребра
-м столбце соответствует принадлежности соответствующего ребра 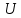 -циклу, а
-циклу, а  об отсутствии ребра.
об отсутствии ребра.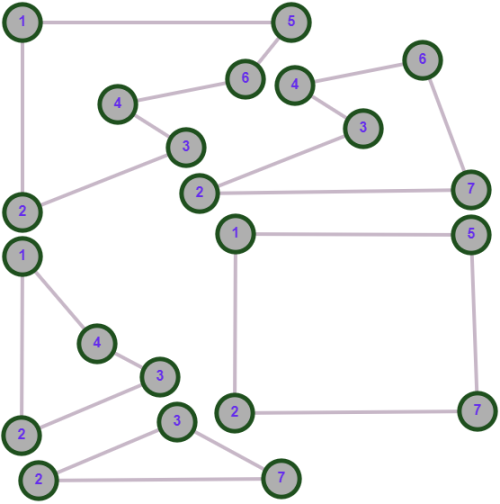
Рисунок 2.2 - Базис, построенный из простых циклов графа А
Количество которых, согласно формуле (1.1) в теореме 1.1 о размерности базиса циклического пространства:
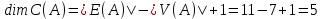
где
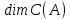 — размерность базиса циклического пространства графа
— размерность базиса циклического пространства графа 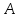 ;
;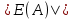 — размерность ребер графа
— размерность ребер графа 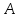 ;
;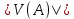 — размерность вершин графа
— размерность вершин графа 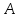 .
.В дополнение к этому, попарно суммируем те базисные элементы из (2.3), длины циклов которых при этом уменьшаются, до тех пор, пока не останется таких базисных пар, таким образом получаем множество порожденных циклов, изображенных на рисунке 2.3, которые, по лемме 1.1, формируют циклическое пространство
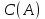 :
: 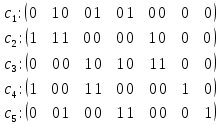 | (2.4) |
где
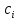 ,
, 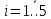 — элемент базиса над полем
— элемент базиса над полем  ,
, 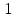 в
в 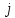 -м столбце соответствует принадлежности соответствующего ребра элементу, а
-м столбце соответствует принадлежности соответствующего ребра элементу, а 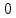 об отсутствии ребра в элементе.
об отсутствии ребра в элементе.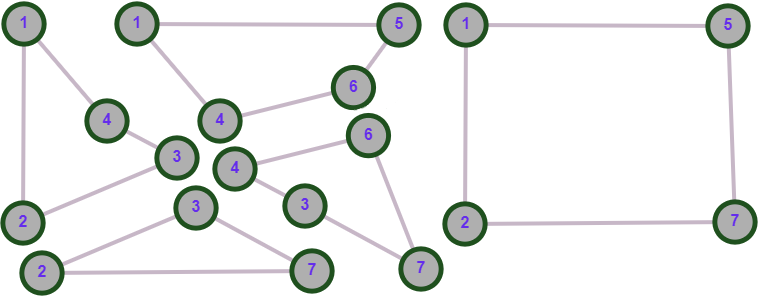
Рисунок 2.3 - Базис, построенный из порожденных циклов графа А
Гамильтонов цикл — это простой цикл, поэтому он принадлежит циклическому пространству
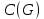 , следовательно равен одному из подмножества множества
, следовательно равен одному из подмножества множества 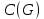 . Количество всех подмножеств, лежащих в
. Количество всех подмножеств, лежащих в 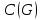 равно
равно 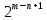 , исключив
, исключив 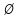 , так как при этом не будет задействован не один цикл, наконец получаем
, так как при этом не будет задействован не один цикл, наконец получаем 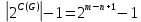 , при условии, что
, при условии, что 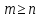 , так как в противном случае граф не является гамильтоновым. Итак, мы имеем верхнюю оценку количества операций, необходимых для поиска цикла Гамильтона., который может быть найден с помощью применения линейной комбинации базисных элементов циклического пространства.
, так как в противном случае граф не является гамильтоновым. Итак, мы имеем верхнюю оценку количества операций, необходимых для поиска цикла Гамильтона., который может быть найден с помощью применения линейной комбинации базисных элементов циклического пространства.Для нашего графа A по формуле о числе подмножеств конечного множества получаем количество различных подмножеств
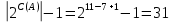 , то есть для получения всех гамильтоновых циклов необходимо перебрать циклическое пространство
, то есть для получения всех гамильтоновых циклов необходимо перебрать циклическое пространство 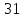 раз.
раз.Перебирая линейные комбинации базисных элементов (2.4), получаем, что граф
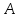 — гамильтонов, а гамильтоновы циклы состоят следующих из сумм:
— гамильтонов, а гамильтоновы циклы состоят следующих из сумм: 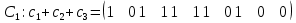 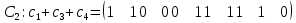 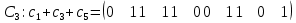 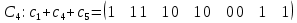 | (2.5) |
где
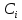 ,
, 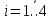 — гамильтонов цикл графа
— гамильтонов цикл графа 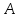 ,
, 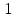 в
в 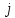 -м столбце соответствует принадлежности соответствующего ребра циклу Гамильтона, а
-м столбце соответствует принадлежности соответствующего ребра циклу Гамильтона, а 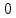 об его отсутствии.
об его отсутствии.Таким образом получаем все гамильтоновы циклы графа (2.5), изображенные на рисунке 2.4, за конечное число операций.
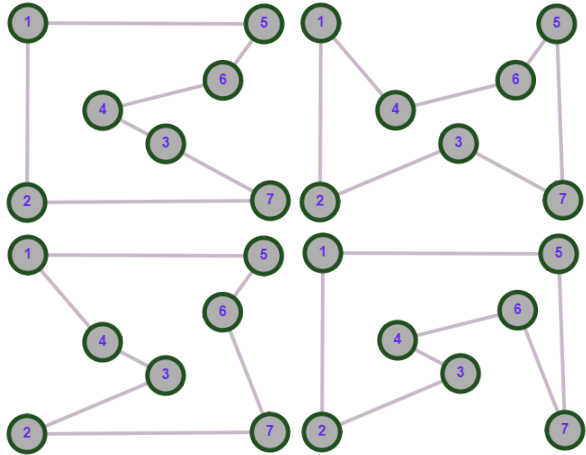
Рисунок 2.4 - Гамильтоновы циклы графа A, слева направо:
2.2 Формализация метода
Пусть
 — неориентированный граф без петель и кратный ребер;
— неориентированный граф без петель и кратный ребер;  — количество его ребер;
— количество его ребер; 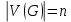 — количество его вершин.
— количество его вершин.Алгоритм по нахождению всех гамильтоновых циклов графа
 состоит в следующем:
состоит в следующем:1) Проверка условий разреженности (2.6) на графе
 и минимального количества ребер (2.7), а именно:
и минимального количества ребер (2.7), а именно: 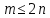 | (2.6) |
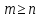 | (2.7) |
Если условия (2.6) и (2.7) выполняются — перейти к пункту 2, иначе — выход из алгоритма с ошибкой: “Граф не удовлетворяет условиям разреженности или минимального количества ребер”.
2) Сформировать матрицу инцидентности
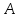 графа G. Перейти к пункту 3.
графа G. Перейти к пункту 3.3) Применить к матричному уравнению (2.8) метод Гаусса над полем по модулю
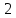 , в получившемся решении
, в получившемся решении 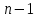 переменных — зависимые и
переменных — зависимые и 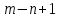 переменных — независимые.
переменных — независимые. 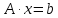 | (2.8) |
где
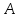 — матрица инцидентности графа
— матрица инцидентности графа  размерности
размерности 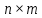 ;
;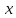 — вектор-столбец, состоящий из
— вектор-столбец, состоящий из 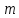 — элементов;
— элементов;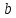 — нулевой вектор-столбец размерности
— нулевой вектор-столбец размерности 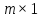 .
.Перейти к пункту 4.
4) В полученной на 3 шаге матрице ступенчатого вида выразить зависимые переменные через независимые, последовательной подстановкой в вектор независимых переменных
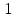 или
или 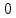 , так чтобы любые два вектора были ортогональны между собой. Векторы
, так чтобы любые два вектора были ортогональны между собой. Векторы 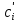 полученных зависимостей есть
полученных зависимостей есть 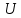 -циклы графа
-циклы графа  , количество которых согласно формуле (1.1):
, количество которых согласно формуле (1.1):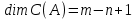
Например, если
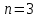 и
и 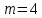 , а
, а 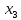 и
и 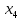 — независимые переменные, то векторы выглядят следующим образом:
— независимые переменные, то векторы выглядят следующим образом: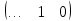
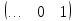
Перейти к пункту 5.
5) Над получившимися
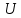 -циклами графа
-циклами графа  попарно применять операцию суммы, до тех пор, пока длинны циклов не перестанут уменьшаться — получим базис циклического пространства
попарно применять операцию суммы, до тех пор, пока длинны циклов не перестанут уменьшаться — получим базис циклического пространства 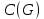 состоящего из множества порожденных циклов
состоящего из множества порожденных циклов 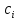 . Перейти к пункту 6.
. Перейти к пункту 6.6) Перебрать все линейные комбинации сумм базисных элементов
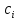 вида:
вида: 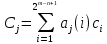 | (2.9) |
где
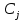 —
— 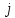 -й цикл из циклического пространства
-й цикл из циклического пространства 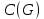 ;
;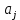 — попарно ортогональные векторы коэффициентов
— попарно ортогональные векторы коэффициентов 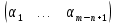 , коэффициент
, коэффициент 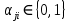 ;
;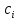 — базисные элементы циклического пространства
— базисные элементы циклического пространства 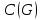 .
.Перейти к пункту 7.
7) Проверить какие из циклов
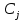 , полученных по формуле (2.9), являются гамильтоновыми. Таким образом мы получили все гамильтоновы циклы графа
, полученных по формуле (2.9), являются гамильтоновыми. Таким образом мы получили все гамильтоновы циклы графа  .
.Последняя проверка требуется из-за возможного случая, изображенного на рисунке 2.5, когда n ребер удовлетворяют нескольким циклам в разных компонентах связности.
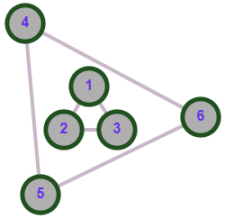
Рисунок 2.5 - Циклы общем длины n с двумя компонентами связности
Полный пример кода для одного из языков программирования, алгоритма по нахождению всех гамильтоновых циклов для неориентированного разряженного графа, приведен в приложении А.
2.3 Оценка алгоритмической сложности метода
Подсчитаем оценку алгоритмической сложности
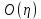 данного метода по нахождению всех гамильтоновых циклов разряженного неориентированного графа.
данного метода по нахождению всех гамильтоновых циклов разряженного неориентированного графа. Во-первых, рассмотрим асимптотическую сложность
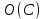 поиска всех базисных элементов циклического пространства
поиска всех базисных элементов циклического пространства 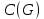 методом Гаусса для системы следующего (матричного) вида:
методом Гаусса для системы следующего (матричного) вида: 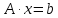 | |
где
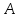 — матрица инцидентности графа
— матрица инцидентности графа  ;
;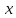 — вектор-столбец;
— вектор-столбец;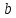 — нулевой вектор-столбец.
— нулевой вектор-столбец.Разобьем вычисления по порядку выполнения на прямой ход метода Гаусса и обратный.
Прямой ход метода Гаусса состоит в последующем исключении неизвестных из линейных уравнений системы. На итерации
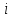 производится исключение неизвестной
производится исключение неизвестной 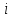 для всех уравнений с индексом
для всех уравнений с индексом 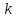 большим чем
большим чем 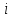 . Для этого для каждого из этих уравнений производится операция суммы над полем
. Для этого для каждого из этих уравнений производится операция суммы над полем 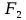 с уравнением
с уравнением 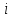 , которое представляет из себя вектор в пространстве
, которое представляет из себя вектор в пространстве 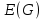 . Поскольку операция производится с каждый элементом строки в количестве
. Поскольку операция производится с каждый элементом строки в количестве 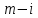 , а обрабатываемых строк
, а обрабатываемых строк 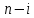 , число операций в прямом ходе Метода Гаусса определяется как:
, число операций в прямом ходе Метода Гаусса определяется как: 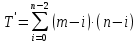 | (2.10) |
где
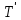 — количество операций прямого хода метода Гаусса.
— количество операций прямого хода метода Гаусса. Для обратного хода на каждой
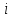 — итерации производится
— итерации производится 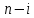 операций суммирования c
операций суммирования c 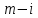 элементами:
элементами: 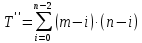 | (2.11) |
где
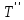 — количество операций обратного хода метода Гаусса.
— количество операций обратного хода метода Гаусса. Следовательно общая вычислительная сложность поиска всех базисных элементов циклического пространства составляет:
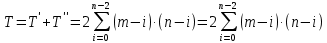 | (2.12) |
где
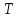 — общее количество операций необходимые для поиска базисных элементов;
— общее количество операций необходимые для поиска базисных элементов;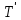 ,
, 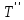 — количество операций (2.10) и (2.11) соответственно.
— количество операций (2.10) и (2.11) соответственно.После раскрытия скобок с использованием формул суммирования, определив член с наибольшей степенью, получаем что асимптотическая сложность равна:
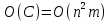 | (2.13) |
где
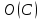 — асимптотическая сложность поиска всех базисных элементов циклического пространства
— асимптотическая сложность поиска всех базисных элементов циклического пространства 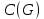 .
.Во-вторых, для получения всех циклов общей длины
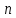 , необходимо перебрать
, необходимо перебрать 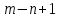 полученных базисных элементов циклического пространства
полученных базисных элементов циклического пространства 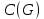 размерность которого равна
размерность которого равна 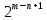 , и следовательно вычислительная сложность равна:
, и следовательно вычислительная сложность равна: 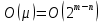 | (2.14) |
где
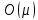 — вычислительная сложность поиска всех циклов общей длины
— вычислительная сложность поиска всех циклов общей длины 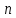 .
.Во-третьих, для определения принадлежности n ребер к гамильтонову циклу, так как по асимптотике поиск цикла совпадает с поиском в глубину, необходимо операций:
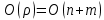 | (2.15) |
где
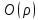 — вычислительная сложность определения принадлежности
— вычислительная сложность определения принадлежности 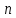 ребер циклу Гамильтона.
ребер циклу Гамильтона. Подытожим общую алгоритмическую сложность, через сложности, вычислительные ранее:
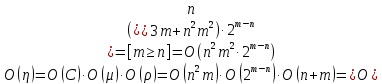 | (2.16) |
где
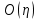 — вычислительная сложность поиска всех гамильтоновых циклов в неориентированном разряженном графе
— вычислительная сложность поиска всех гамильтоновых циклов в неориентированном разряженном графе  без кратных ребер и петель;
без кратных ребер и петель;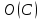 ,
, 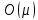 ,
, 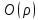 — оценки (2.13), (2.14), (2.15) соответственно.
— оценки (2.13), (2.14), (2.15) соответственно.ЗАКЛЮЧЕНИЕ
Среди задач, имеющих экспоненциальную и факториальную сложность решения по времени, крайне важно выделять те классы, которые в зависимости от подхода могут быть решены за более приемлемое время, чем с применением некоторого спектра базовых методов, тем самым снижая общую нагрузку на вычислительную производительность.
В ходе написания курсовой на основе теории свойств циклического пространства и пространства разрезов, доказаны формулы, и зависимости циклического пространства с размерностью ребер и вершин графа определенного класса разряженных графов. С применением алгебраических методов продемонстрирована постановка и дальнейшая разработка метода по нахождению всех гамильтоновых циклов для разряженного неориентированного графа.
Изучена научная литература и основные теоретические аспекты исследования, посредством которых раскрыты ключевые понятия, дополненные поясняющими иллюстрациями; и практическое применение общего класса задач на графах.
Разработан метод, имеющий, кроме абстрактного приложения, применение на практике для матриц, построенных, например, для транспортной сети или сети интернет с каналами передачи данных для каждой из сторон. В частности, если необходимо передать какую-то информацию от сервера до всех пользователей частной сети, таблица маршрутизации которых, обычно, разряжена, а затем вернуть завершающий сигнал на сервер, то, если для такой сети выполняются условия данного метода, можно предварительно применить описанный в данной работе метод, а затем с помощью полученных данных о гамильтоновых циклах настроить маршрутизаторы и получить эффективный способ передачи. Применение находит себя так же в криптографии, где из-за NP сложности задачи нахождения гамильтонова цикла, расшифровывающий ключ кодируется в виде цикла Гамильтона. Далее надлежит сформировывать циклы так, чтобы они удовлетворяли условиям данного метода и расшифровывать закодированную информацию эффективным образом.
Исследована и выведена вычислительная сложность метода, позволяющая перед применением метода получить оценку производительности и сравнить ее с другими методами. Оценка имеет свои особенности, отталкивающиеся от количественного соотношения ребер графа, и дает эффективный результат на определенном классе графов по сравнению с вычислительной сложностью распространенных комбинаторных методов, опирающихся на количество узлов графа.
Описан и протестирован алгоритм на одном из актуальных языков программирования с применением битовых операций, которые посредством ускорения основной операции суммирования векторов и более компактного представления матриц улучшают алгоритмическую производительность алгоритма в целом.
Разработанный метод базируется на доказанной теории поэтому устойчив и не дает сбоев, и доступен для понимания без дополнительного углубления в теорию.
СПИСОК ЛИТЕРАТУРЫ
1) Андерсон, Д.А. Дискретная математика и комбинаторика. / Д.А. Андерсон; ред. С.Н. Тригуб; пер. с англ. М.М. Беловой — М., СПб: ООО “И.Д. Вильямс”, 2004. − 960 с.
2) Ерусалимский, Я. М.: Дискретная математика. Теория и практикум. / Я. М. Ерусалимский — СПб: Лань, 2018. — 476 с.
3) Зыков, А. А. Основы теории графов / А. А. Зыков. — М.: Вуз овская книга, 2004. — 662 c.
4) Karp, R.M. Reducibility among combinatorial problems, Complexity of Computer Computations / R.M. Karp — Plenum Press, 1972. — pp.85-103. DOI: 10.1007/978-3-540-68279-0_8
5) Кузнецов, О. П. Дискретная математика для инженера / О. П. Кузнецов. — 6-е изд., стер. — СПб.: Лань, 2009. 400 с.
6) Курош, А.Г. Курс высшей алгебры. / А.Г. Курош — 21-е изд., — СПб.: Лань, 2020. — 432 с.
7) Микони, С. В. Дискретная математика для бакалавра: множества, отношения, функции, графы: учебное пособие для вузов / С. В. Микони. — СПб: Лань, 2012. — 186 с.
8) Новиков, Ф.А. Дискретная математика: Учебник для вузов. / Ф.А. Новиков — 2-е изд., — СПб.: Питер, 2013. — 432 с.
9) Новиков, Ф.А. Дискретная математика для программистов. / Ф.А. Новиков — 3-е изд., — СПб.: Питер, 2009. — 384 с.
10) Оре, О. Теория графов. / О. Оре; ред. Н.Н. Воробьeв; пер. с англ. И.Н. Врублевской — 2-е изд., стер. — М.: Наука, 1980. — 336 с.
11) Панюкова, Т.А. Комбинаторика и теория графов / Т.А. Панюкова — 3-е изд. — М.: Ленанд, 2017. — 216 с.
12) Просветов, Г. И. Дискретная математика. Задачи и решения: учебное пособие / Г. И. Просветов. — М.: БИНОМ. Лаборатория знаний, 2008. — 222 с.
13) Седжвик, Р., Уэйн, К. Алгоритмы на Java / Р. Седжвик; К. Уэйн; ред. С.Н. Тригуб; пер. с англ. А.А. Моргунова — 4-е изд. — М., СПб: ООО “И.Д. Вильямс”, 2013. — 848 c.
14) Стенли, Р. Перечислительная комбинаторика. / Р. Стенли; ред. А.М. Вершик; пер. с англ. А.И. Барвинка и А.А. Лодкина. — M.: Мир — 1990. — 440 c.
15) Фаддеев, Д. К. Лекции по алгебре / Д. К. Фаддеев— Изд. 4-е., стереотип. — СПб.: Лань, 2005. - 416 с.
16) Хаггарти, Р. Дискретная математика для программистов. / Р. Хаггарти; ред. С. А. Кулешова; пер. с англ. — М.: Техносфера, 2003. — 320 с.
17) Харари, Ф. Теория графов / Ф. Харари; ред. Г. П. Гаврилов; пер. с англ. В. П. Козырева — 5-е изд. — М.: Ленанд, 2018. — 297 с.
18) Яблонский, С.В. Введение в дискретную математику: учебное пособие для вузов / С. В. Яблонский — 5-е изд. — М.: Высшая школа, 2008. — 384 с.
19) Карпов, В.Д. Теория графов [Электронный ресурс] / В.Д. Карпов —Электрон. текстовые дан. — СПб.: [б.и.], 2009. — Режим доступа: https://logic.pdmi.ras.ru/dvk/graphs_dk.pdf, свободный.
20) Хитров, Г. М. Теория графов. ГрафоMann [Электронный ресурс] / Г. М. Хитров — Электрон. текстовые дан. — СПб.: [б.и.], 2013. — Режим доступа: http://www.apmath.spbu.ru/grafomann/, свободный.
ПРИЛОЖЕНИЕ А
Реализации алгоритма на языке программирования Java, с использованием побитовых операций
Приведенный алгоритм печатает все гамильтоновы циклы графа, либо дополнительную информацию об их отсутствии или не выполнении начальных условий:

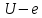 содержит две компоненты связности —
содержит две компоненты связности — 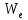 и
и 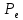 .
. 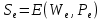 .
.  содержит только один цикл
содержит только один цикл