КонтрольнаяГидравлика. Основные физические свойства жидкостей. Их размерности в системе си
 Скачать 290.94 Kb. Скачать 290.94 Kb.
|
|
Задание 1 Ответить на теоретические вопросы: Основные физические свойства жидкостей. Их размерности в системе СИ. Ответ Жидкость - физическое тело, которое обладает свойством текучести, т. е. не имеющее способности самостоятельно сохранять свою форму.Текучесть жидкости обусловлена подвижностью молекул, составляющих жидкость. Жидкостью называется агрегатное состояние вещества, промежуточное между твердым и газообразным. Жидкость характеризуется следующими свойствами: 1) сохраняет объем; 2) образует поверхность; 3) обладает прочностью на разрыв; 4) принимает форму сосуда; 5) обладает текучестью. Свойства жидкости с 1) по 3) подобны свойствам твёрдых тел, а свойство 4) - свойству жидкости. Жидкости, законы движения и равновесия которых изучаются в гидравлике (механике жидкости и жидкости), делятся на два класса: сжимаемые жидкости или газы, почти несжимаемые - капельные жидкости. В гидравлике рассматриваются как идеальные, так и реальные жидкости. Идеальная жидкость - жидкость, между частицами которой отсутствуют силы внутреннего трения. Вследствие этого такая жидкость не сопротивляется касательным силам сдвига и силам растяжения. Идеальная жидкость совершенно не сжимается, она оказывает бесконечно большое сопротивление силам сжатия. Такой жидкости в природе не существует - это научная абстракция, необходимая для упрощения анализа общих законов механики применительно к жидким телам. Реальная жидкость - жидкость, которая не обладает в совершенстве свойствами идеальной жидкости, она в некоторой степени сопротивляется касательным и растягивающим усилиям, а также отчасти сжимается. Для решения многих задач гидравлики этим отличием в свойствах идеальной и реальной жидкостей можно пренебречь. В связи с этим физические законы, выведенные для идеальной жидкости, могут быть применены к жидкостям реальным с соответствующими поправками. Ниже кратко представлены общие сведения, касающиеся физических свойств жидкостей. Плотность — это отношение массы вещества к его объему: р = m/V На плотность жидкости влияют температура и давление. Удельный вес — это отношение веса жидкости к занимаемому объему: у = mg/V = pg. Удельный объем жидкости — объем единицы массы этой жидкости: v = У/m = 1/р. Температурное расширение — свойство жидкости изменять свой объем при изменении температуры. С ростом температуры объем жидкости увеличивается и наоборот. Различные жидкости при увеличении температуры на одну и ту же величину увеличиваются в объеме по разному. Поэтому свойство жидкости увеличиваться в объеме с увеличением температуры характеризуется коэффициентом температурного расширения Bт, который показывает изменение единицы объема данной жидкости при изменении ее температуры на 1 К. Увеличение объема при нагревании рассчитывается по уравнению: Δ V= Bт*V0*Δ Т где V0 начальный объем жидкости; дельта Т— изменение температуры. В расчетах ДВС коэффициент температурного расширения считают постоянным, хотя на самом деле он зависит от условий нагревания или охлаждения, давления и начальной температуры. Сжимаемость — свойство жидкости изменять объем при изменении давления. Δ V = Bр*V0*Δ р, где дельта V— изменение объема; дельта р — изменение давления; Вр — коэффициент объемного сжатия. Коэффициент объемного сжатия показывает изменение единицы объема жидкости при изменении давления на 1 Па. Он зависит от условий сжатия, температуры и начального давления. При расчетах эта зависимость не учитывается. Коэффициент объемного сжатия для воды равен 5 * 10-4 1/Па, для нефтепродуктов — 7*10-4 1/Па, для ртути — 0,3*10-4 1/Па. Ввиду незначительных величин жидкости считаются несжимаемыми. Вязкость — свойство жидкости оказывать сопротивление перемещению одной ее части относительно другой. Динамическая вязкость учитывает свойства жидкости, от которых зависит ее внутреннее трение. В технике и в частности в гидравлике часто используется кинематическая вязкость v, которая равна отношению динамической вязкости жидкости к ее плотности: v = n/p Для упрощения решения гидродинамических задач считают, что рассматриваемые жидкости не обладают температурным расширением, сжимаемостью и вязкостью. Такие жидкости в отличие от реальных называются идеальными. В чем отличие жидкостей от твердых тел и газов. Ответ: Молекулы в газах находятся далеко относительно друг друга, расстояния между молекулами примерно раз в десять больше самих молекул. Поэтому молекулы не взаимодействуют между собой, не устанавливается межмолекулярных связей. Молекулы беспорядочно двигаются во все стороны. В результате газ не имеет формы, занимает весь предоставленный ему объем, легко сжимается и расширяется. Если наполнить резиновый мяч воздухом, то воздух равномерно заполнит весь его объем, он не осядет внизу или не поднимется в верхнюю его часть. Он распространится именно по всему объему. Если тем же объемом воздуха заполнить мяч, который больше первого, то воздух в нем также заполнит весь объем, но будет менее плотный. Поэтому нам будет легче сжать второй мяч. Молекулы жидкости (например, воды), в отличие от молекул газа, находятся близко друг к другу (можно сказать, вплотную) и взаимодействуют между собой. Однако молекулы жидкости, также, как и у газа, могут свободно перемещаться. Это обуславливает следующие свойства жидкости: сохраняет свой объем, а не занимает весь объем сосуда, принимает форму сосуда, в которой находится, обладает текучестью, очень плохо сжимается. В отличие от жидкостей, в твердых телах молекулы чаще всего расположены упорядочено. Они не могут беспорядочно менять свое положение. Поэтому твердые тела, в отличие от жидкостей, не обладают текучестью, а сохраняют свою форму. Однако следует сделать одну оговорку. Это так по отношению к твердым телам, чье молекулярное строение представляет собой кристаллическую решетку. Аморфные тела обладают текучестью, но намного меньшей, чем у жидкостей. Молекулы или атомы кристаллических тел расположены друг относительно друга упорядоченно. Существует определенное «правило», по которому каждая молекула (или атом) соединяется с другими молекулами кристалла. Так молекулы могут располагаться в вершинах кубов или шестиугольников. В аморфных телах молекулы располагаются беспорядочно. Задача 1. В вертикальном стальном резервуаре, заполненном наполовину, хранится нефть (рис.1). Плотность нефти, при начальной температуре, равна 855 кг/м3. Определить массу хранящейся нефти и колебания ее уровня в резервуаре, если температура в течение года принимает значения от t1= -150С (зима) до t2=200С (лето). Коэффициент температурного расширения αТ =0,0006 1/0С, вид резервуара РВС-1000. Решение Так как резервуар заполнен наполовину, то объем хранящейся в нем нефти равен 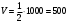 м3. Соответственно, масса хранящейся нефти равна м3. Соответственно, масса хранящейся нефти равна 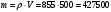 кг. кг. Колебание уровня нефти равно 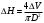 , где , где 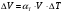 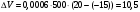 м3 м3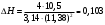 м мОтвет: 427500 кг, 0,103 м Задание 2 Ответить на теоретические вопросы: Объясните понятия абсолютного и избыточного давления, вакуума. Какими приборами измеряется давление, вакуум. Устройство и принцип работы этих приборов. Ответ Превышение давления в точке над атмосферным давлением называется избыточным или манометрическим давлением (pм, pизб). Введение такого понятия необходимо, так как манометры реагируют только на отклонения измеряемого давления от атмосферного. Пружинный манометр (рис. 1) состоит из корпуса 1, в котором размещена одновитковая полая трубчатая пружина 2. Внутри полой трубчатой пружины измеряемое давление, а снаружи атмосферное. Трубчатая пружина одним своим концом жестко соединена с входным штуцером 7, имеющим отверстие для пропуска жидкости в полость трубчатой пружины. Свободный конец трубчатой пружины поводком 6 шарнирно соединен с кулисой сектора 5, зубчатый сектор 4 входит в зацепление с шестеренкой 3, посаженной на валу указательной стрелки 8. Для визуального наблюдения и настройки предусмотрена шкала 10. 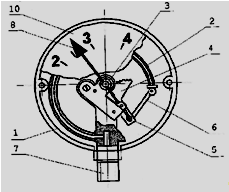 Рис.1. Пружинный манометр. Принцип работы манометра основан на изменении положения трубчатой пружины. При повышении давления она стремиться распрямиться. Тянет за собой поводок 6, движение которого посредством шарнирного механизма с зубчатой парой преобразуется во вращательное движение вала стрелки. При снижении давления под действием сил упругой деформации пружина возвращается в исходное состояние, стрелка совершает поворот в обратном направлении. Угол поворота стрелки пропорционален измеряемому давлению. Чувствительным элементом манометра (вакуумметра) может быть и мембрана или сильфон, но и в этом случае приборы реагируют на отклонение давления от атмосферного. Абсолютное (или полное) давление pабс - это сумма избыточного и атмосферного давлений. Вакуумом (pвак) называется недостаток абсолютного давления до атмосферного. Для наглядности покажем диаграмму давлений (рис. 2.). В технике, если измеряемое давление выше атмосферного, пользуются понятием манометрического давления, а если ниже атмосферного - то понятием вакуума. 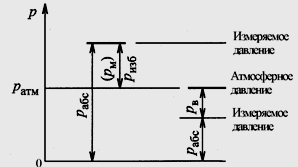 Рис. 2. Диаграмма давлений Предположим, что имеем закрытый резервуар с жидкостью (рис. 3). 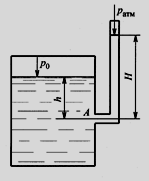 Рис. 3. Определение пьезометрической высоты Если в точке А к резервуару присоединить открытую в атмосферу трубку, то в такой трубке жидкость поднимется на некоторую высоту H, большую или меньшую глубины воды в резервуаре в зависимости от того, будет ли p0 больше или меньше pатм. Такие трубки называются пьезометрами, а высоту Н называют пьезометрической высотой или пьезометрическим напором. Пьезометрическая высота характеризует давление или, точнее говоря, измеряет его в линейных единицах. Для доказательства проведем через точку А поверхность равного давления - горизонтальную плоскость. В соответствии с уравнением (1) давление в любой точке этой поверхности равно: p0 + gh = pатм + gH(1) 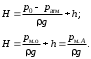 (2) (2)Для пьезометров (жидкостных манометров) применяют стеклянные трубки диаметром не менее 5-10 мм в целях избежания явлений капиллярного поднятия, обусловленного действием поверхностного натяжения, смачиваемостью. Недостаток абсолютного давления до атмосферного (т.е. вакуум) также можно измерить высотой столба жидкости. Предположим, что в сосуде А (рис. 4.) абсолютное давление ниже атмосферного. Соединим сосуд А с открытым сосудом с помощью стеклянной трубки. Жидкость в трубке поднимется на некоторую высоту hвак. Для определения hвак проведем поверхность уровня, совпадающую со свободной поверхностью жидкости в открытом сосуде. Давления во всех точках этой поверхности, в том числе и в точках В и С, равны. Тогда, pА + ρghвак = pатм(3) 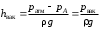 (4) (4)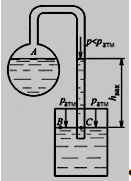 Рис.4. Вакуумметр. Высоту столба жидкости, характеризующую вакуум (hвак), называют вакуумметрической. Рассмотрим покоящуюся жидкость в закрытом резервуаре с давлением на свободной поверхности p0 (рис. 5). Выберем в этом резервуаре две произвольные точки А и В и установим в каждой из них по пьезометру. Для сопоставления величин примем плоскость сравнения, следом которой пусть будет линия 0-0. Обозначим координаты или отметки точек А и В по отношению к плоскости сравнения через ZА и ZВ. Если гидростатическое давление в этих точках обозначить через pА и pВ, то пьезометрические высоты в пьезометрах А и В соответственно будут равны 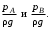 Суммы высот 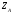 и и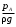 или или 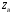 и и 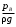 называются гидростатическим напором в данной точке жидкости относительно выбранной плоскости сравнений 0-0. Согласно уравнению (5) эти суммы равны между собой. называются гидростатическим напором в данной точке жидкости относительно выбранной плоскости сравнений 0-0. Согласно уравнению (5) эти суммы равны между собой.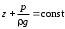 (5) (5)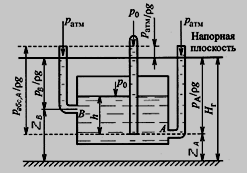 Рис. 5. Определение гидростатического напора. Следовательно, для данного объема жидкости гидростатический напор Н относительно выбранной плоскости сравнения есть величина постоянная, или 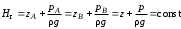 . (6) . (6)Любые пьезометры, и в частности А и В (см. рис. 5), по существу, являются сообщающимися сосудами, и поэтому поверхности жидкости в них будут находиться в одной горизонтальной плоскости, которая называется напорной плоскостью. 2. Вывод основного уравнения гидростатики и его физический смысл. Что такое поверхность равного давления и каким уравнением она описывается? Что является поверхностью равного давления для жидкости в поле сил тяжести? Ответ Рассмотрим распространенный случай равновесия жидкости, когда на нее действует только одна массовая сила – сила тяжести, и получим уравнение, позволяющее находить гидростатическое давление в любой точке рассматриваемого объема жидкости. Это уравнение называется основным уравнением гидростатики. Пусть жидкость содержится в сосуде (рис.6) и на ее свободную поверхность действует давление P0. Найдем гидростатическое давление P в произвольно взятой точке М, расположенной на глубине h. 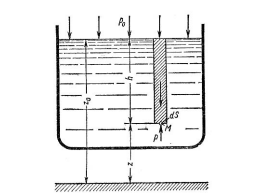 Рисунок 6 Выделимоколо точки М элементарную горизонтальную площадку dS и построим на ней вертикальный цилиндрический объем жидкости высотой h. Рассмотрим условие равновесия указанного объема жидкости, выделенного из общей массы жидкости. Давление жидкости на нижнее основание цилиндра теперь будет внешним и направлено по нормали внутрь объема, т.е. вверх. Запишем сумму сил, действующих на рассматриваемый объем в проекции на вертикальную ось: 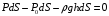 Последний член уравнения представляет собой вес жидкости, заключенный в рассматриваемом вертикальном цилиндре объемом hdS. Силы давления по боковой поверхности цилиндра в уравнение не входят, т.к. они перпендикулярны к этой поверхности и их проекции на вертикальную ось равны нулю. Сократив выражение на dS и перегруппировав члены, найдем 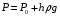 Полученное уравнение называют основным уравнением гидростатики. По нему можно посчитать давление в любой точке покоящейся жидкости. Это давление, как видно из уравнения, складывается из двух величин: давления P0 на внешней поверхности жидкости и давления, обусловленного весом вышележащих слоев жидкости. Из основного уравнения гидростатики видно, что какую бы точку в объеме всего сосуда мы не взяли, на нее всегда будет действовать давление, приложенное к внешней поверхности P0. Другими словами давление, приложенное к внешней поверхности жидкости, передается всем точкам этой жидкости по всем направлениям одинаково. Это положение известно под названием закона Паскаля. Поверхность, во всех точках которой давление одинаково, называется поверхностью уровня/ В обычных условиях поверхности уровня представляют собой горизонтальные плоскости. Решить задачу: Какое усилие необходимо приложить к окончанию рычага гидравлического пресса (F), чтобы поднять груз массой G=1500 кг, при условии, что диаметр меньшего поршня d=150 мм, а диаметр большего поршня D=310 мм. Плечи рычага a=0,3 м и b=1,2 м. Силой трения пренебречь. Решение 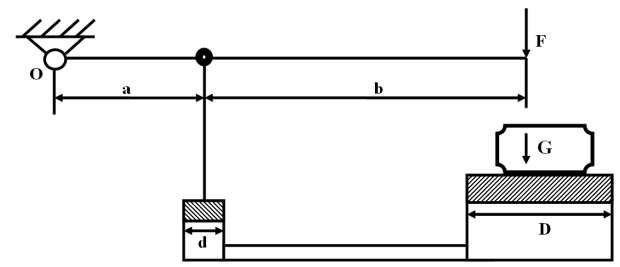 Уравнение моментов сил, приложенных к рычагу относительно точки О: 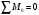 Имеем: 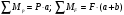 Откуда: 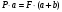 и и 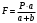 Из закона Паскаля следует: 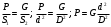 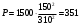 Н НИскомое усилие: 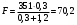 Н НОтвет: 70,2 Н Задание 3 Ответить на теоретические вопросы: Гидростатическое давление и его свойства. Что такое “эпюра давления”? Принцип построения эпюр давления. Использование эпюр давления для определения величины гидростатического давления и центра давления. Ответ Гидростатическое давление – это давление, производимое на жидкость силой тяжести. Эпюра давления — это графическое изображение распределения гидростатического давления по стенке или по длине какого-либо контура
Методика определения силы и центра давления жидкости на цилиндрические поверхности. Ответ Задача определения результирующей силы гидростатического давления на плоскую фигуру сводится к нахождению величины этой силы и точки ее приложения или центра давления. Представим резервуар, наполненный жидкостью и имеющий наклонную плоскую стенку (рис. 8). На стенке резервуара наметим некоторую плоскую фигуру любого очертания площадью . Координатные оси выберем так, как указано на чертеже. Ось ОZ перпендикулярна к плоскости чертежа. В плоскости оуz расположена рассматриваемая фигура, которая проектируется в виде прямой, обозначенной жирной линией, справа показана эта фигура в совмещении с плоскостью оуz. В соответствии с 1-м свойством гидростатического давления можно утверждать, что во всех точках площади давление жидкости направлено нормально к стенке. Отсюда заключаем, что сила гидростатического давления, действующая на произвольную плоскую фигуру, также направлена нормально к ее поверхности. 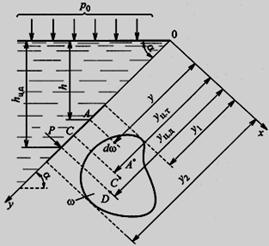 Рис. 8. Давление жидкости на плоскую стенку. Для определения силы давления выделим элементарную (бесконечно малую) площадку d. Силу давления dP на элементарную площадку определим так: dP = pd = (p0 + gh)d (7) где h - глубина погружения площадки d. Так как h = ysin, то dP =pd = (p0 + gysin)d. Сила давления на всю площадку : Первый интеграл представляет собой площадь фигуры : Второй интеграл представляет собой статический момент площадки относительно оси х. Как известно, статический момент фигуры относительно оси х равен произведению площади фигуры на расстояние от оси х до центра тяжести фигуры, т.е.: Подставляя в уравнение (8) значения интегралов, получаем P = po + gsinyц.т(11) Но так как yц.т sin = h ц.т - глубина погружения центра тяжести фигуры, то: P = (p0 + ghц.т) (12) Выражение, заключенное в скобки, представляет собой давление в центре тяжести фигуры: p0 + ghц.т = pц.т (13) Следовательно, уравнение (12) можно записать в виде P = pц.т (14) Таким образом, сила гидростатического давления на плоскую фигуру равна гидростатическому давлению в центре тяжести ее, умноженному на величину площади этой фигуры. Определим центр давления, т.е. точку приложения силы давления Р. Так как поверхностное давление , передаваясь через жидкость, равномерно распределяется по рассматриваемой площади, то точка приложения силы будет совпадать с центром тяжести фигуры. Если над свободной поверхностью жидкости давление атмосферное (p0 = pатм), то его учитывать не надо. Давление, обусловленное весом жидкости, неравномерно распределяется по площади фигуры: чем глубже расположена точка фигуры, тем большее давление она испытывает. Поэтому точка приложения силы P = ghц.т будет лежать ниже центра тяжести фигуры. Координату этой точки обозначим yц.д. Для ее нахождения воспользуемся известным положением теоретической механики: сумма моментов составляющих элементарных сил относительно оси ох равна моменту равнодействующей силы Р относительно той же оси ох, т.e. так как dP = ghd = gysind, то Здесь значение интеграла представляет собой момент инерции фигуры относительно оси ох: а сила Подставляя эти соотношения в уравнение (16), получаем yц.д = Jx / yц.т. (17) Формулу (17) можно преобразовать, воспользовавшись тем, что момент инерции Jx относительно произвольной оси ох равен Jx = J0 + y2ц.т (18) где J0 - момент инерции площади фигуры относительно оси, проходящей через ее центр тяжести и параллельной оси ох; yц.т - координата центра тяжести фигуры (т.е. расстояние между осями). С учетом формулы (17) получим: 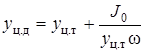 . (19) . (19)Уравнение (19) показывает, что центр давления, обусловленный весовым давлением жидкости, всегда расположен ниже центра тяжести рассматриваемой фигуры на величину и погружен на глубину 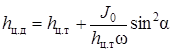 (20) (20)где hц.д = yц.д sin - глубина погружения центра давления. Решить задачу: Определить на какой высоте z установится уровень ртути в сосуде относительно точки А, если манометрическое (избыточное) давление в этой точке составляет Pa=1,1 Атм . Жидкости находится в равновесии. Плотность ртути принять равной 13 600 кг/м3 , воды 990 кг/м3 . Значение высоты h=45 см. Решение Абсолютное (полное) гидростатическое давление находится как сумма давления, приложенного к поверхности жидкости (P0), и давления столба жидкости (Pизб) высотой, равной глубине погружения клапана. Рабс=Р0+Ризб=Р0+𝜌𝑔ℎ,[Па] где P0 – давление, приложенное к поверхности жидкости, Па; 𝜌 - плотность жидкости, кгм3; g – ускорение свободного падения, м/с2; h – высота столба жидкости, м. Рабс=Р0+Ра= Р0+𝜌рт𝑔ℎ+𝜌ж𝑔z , где Р0=0, тогда Ра= 𝜌рт𝑔ℎ+𝜌ж𝑔z, z= (Ра - 𝜌рт𝑔ℎ)/𝜌ж𝑔= (111457 -(13600*10*0,45))/(990*10) =5,08 м. Задание 5 Ответить на теоретические вопросы: 1.Как определяется средняя скорость в живом сечении потока? Что такое гидравлический радиус и гидравлический диаметр и зачем введены эти понятия? Чем отличается равномерное движение от неравномерного? Понятие идеальной жидкости. Ответ Поток – масса движущейся жидкости, направляемая твердыми стенками. w1 и w2 – скорости частиц 1 и2.  Линия тока – линия, в каждой точке которой вектор скорости частицы совпадает с направлением касательной (линия 1-2-3). Линия тока – линия, в каждой точке которой вектор скорости частицы совпадает с направлением касательной (линия 1-2-3).Трубка тока – совокупность линий тока, проведенных через все точки контура элементарного живого сечения Элементарная струйка – пучок линий тока, проходящих через трубку тока. Живое сечение потока – поперечное сечение потока плоскостью, нормальной к направлению скорости жидкости (S). Смоченный периметр – часть контура живого сечения, по которой поток соприкасается с твердыми стенками (П). Гидравлический радиус потока Rг – отношение площади живого сечения S к соченному периметру П: Эквивалентный диаметр dэ равен учетверенному гидравлическому радиусу: dэ Абсолютная шероховатость стенок ? - это средняя высота выступов неровностей, измеренная в линейных единицах. Относительная шероховатость Расход жидкости – количество жидкости, протекающей через живое сечение потока в единицу времени. Объемный расход измеряется в Максимальна около оси трубы, а по мере приближения к стенкам она уменьшается. В расчетах обычно используют среднюю скорость. Средняя скорость движения потока равна отношению объемного расхода к площади живого сечения потока: объемный расход массовый расход Скорость жидкости в данной точке – местная (локальная) скорость. 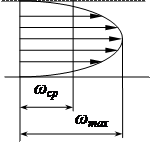 4. Движение жидкости может быть установившимся (стационарным) и неустановившимся (нестационарным). При нестационарном движении параметры жидкости (давление, скорость) зависят от времени, при стационарном – не зависят. Напорное движение - поток полностью заполняет поперечное сечение трубы, безнапорное – неполностью. Равномерное движение – вдоль трубы скорость жидкости постоянна, неравномерное – переменна. Впервые режимы течения жидкости изучались Рейнольдсом в 1883г. Режим движения жидкости может быть ламинарным (струйчатым) или турбулентным (вихревым). При ламинарном режиме все частицы жидкости движутся по параллельным траекториям, поперечное перемешивание отсутствует. При турбулентном режиме частицы жидкости движутся по хаотическим траекториям, хотя вся масса жидкости перемещается в одном направлении. Переход от ламинарного режима к турбулентному происходит тем легче, чем больше массовая скорость жидкости и диаметр трубы и тем меньше вязкость жидкости Критерий Рейнольдса Re: Он является мерой соотношения между силами вязкости и инерции в движущемся потоке. Переход от ламинарного режима к турбулетному характеризуется критическим значением Re. Для прямых гладких труб при Re10000 – устойчивый (развитый) турбулентный режим. Для ламинарного режима wср=0,5wmax, для турбулентного - wср=(0,85-0,9)wmax.. 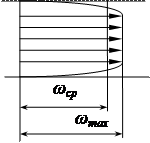 Рис. эпюра скоростей для турбулентного режима. Непосредственно у самой стенки тербулентного потока имеется ламинарный подслой очень малой толщины δ. В пределах этого слоя происходит резкий рост скорости от нуля на стенке до конечной величины на ее границе. При дальнейшем удалении от стенки происходит переход в турбулентное ядро. 5. При условии недеформируемости и непроницаемости стенок для потока жидкости можно записать (для стационарного режима): Для несжимаемой жидкости (ρ=const): Уравнение постоянства расхода выражает материальный баланс потока и является частным случаем закона сохранения массы. Скорость частиц жидкости максимальна около оси трубы, а по мере приближения к стенкам она уменьшается. В расчетах обычно используют среднюю скорость. Средняя скорость движения потока равна отношению объемного расхода к площади живого сечения потока: объемный расход массовый расход Скорость жидкости в данной точке – местная (локальная) скорость. 2. Приведите вывод уравнения неразрывности для элементарной струйки и для потока жидкости и объясните его физический смысл. Ответ Определим уравнения неразрывности потока.  Отделим сечениями 1-1 и 2-2 некоторый отрезок элементарной струйки. В этот отрезок в единицу времени через сечение 1-1 втекает объем жидкости равный Q1 = υ1 * F1, а через сечение 2-2 из него же вытекает объем, равный Q2 = υ2 * F2. Примем, что жидкость несжимаема и что в ней невозможно образование незаполненных жидкостью пространств – т.е. будем считать, что соблюдается условие сплошности или неразрывности движения. Учитывая, что форма элементарной струйки с течением времени не изменяется и поперечный приток в струйку или отток из ней отсутствуют, приходим к выводу, что элементарные расходы жидкости, проходящие через сечение 1-1 и 2-2, должны быть одинаковы. Таким образом Q1 = Q2 Или υ1 * F1 = υ2 * F2 Такие соотношения можно составить для любых двух сечений струйки. Поэтому в более общем виде получаем, что всюду вдоль струйки Q = υ * F = const. Это уравнение называется уравнением неразрывности жидкости – оно является первым основным уравнением гидродинамики. Переходя далее к потоку жидкости в целом получаем, что υ1 / υ2 = F2 / F1 т.е. средние скорости в поперечных сечениях потока при неразрывности движения обратно пропорциональны площади этих сечений. Решить задачу: Определить, какое необходимо создать давление с помощью насоса, чтобы лафетный ствол обеспечивал расход равный Q. Потерями напора местными и по длине пренебречь. Диаметр выходного отверстия лафетного ствола d принять по таблице. Схема подсоединения лафетного ствола показана на рисунке 9. Плотность воды 1000 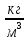 . .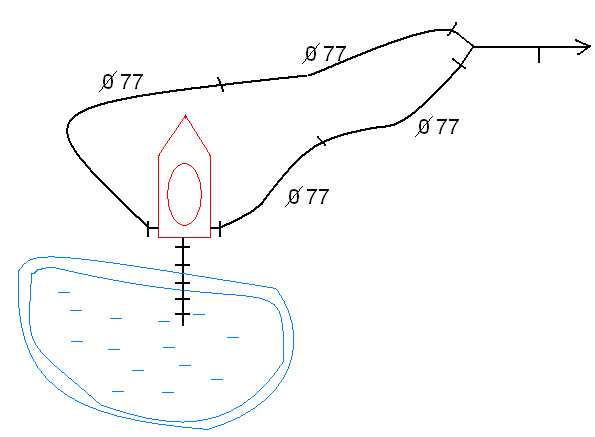 Рис. 9. Рисунок к задаче № 5. Исходные данные к задаче d= 28 мм Q=29 л/с Решение Уравнение Бернули: 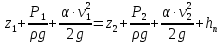 z1=z2; P2=0; α=1 Так как по условию задачи потерями напора по длине можно пренебречь, принимаем hп = 0. Таким образом, уравнение примет вид: 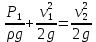 откуда, 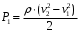 Учитывая, что 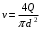 , получим , получим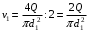 ; ; 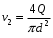 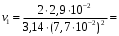 3,1 м/с; 3,1 м/с; 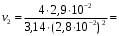 47,1 м/с 47,1 м/с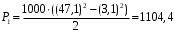 Па ПаОтвет: 1104,4 Па Задание 6 Ответить на теоретические вопросы: Приведите уравнения движения идеальной и реальной жидкости и поясните, что характеризуют отдельные их члены. Ответ Идеальной называют воображаемую жидкость, лишенную вязкости и теплопроводности. В ней отсутствует внутреннее трение, она непрерывна и не имеет структуры. Одно из важнейших уравнений гидромеханики было получено в 1738 г. швейцарским учёным Даниилом Бернулли (1700 - 1782). Ему впервые удалось описать движение идеальной жидкости, выраженной в формуле Бернулли. Уравнение стационарного движения, носящее его имя, имеет вид: 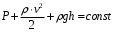 где P - давление жидкости, ρ − её плотность, v - скорость движения, g - ускорение свободного падения, h - высота, на которой находится элемент жидкости. ρ⋅v2/2 - динамическое давление - кинетическая энергия единицы объёма движущей жидкости; ρ⋅g⋅h - весовое давление - потенциальная энергия единицы объёма жидкости; P - статическое давление, по своему происхождению является работой сил давления и не представляет собой запаса какого-либо специального вида энергии ("энергии давления"). Это уравнение объясняет почему в узких участках трубы растёт скорость потока и падает давление на стенки трубы. Максимальное давление в трубах устанавливается именно в месте, где труба имеет наибольшее сечение. Узкие части трубы в этом отношении безопасны, но в них давление может упасть настолько, что жидкость закипит, что может привести к кавитации и разрушению материала трубы. Уравнение Бернулли для потока реальной жидкости несколько отличается от приведённого выше уравнения идеальной жидкости. Дело в том, что при движении реальной вязкой жидкости возникают силы трения, на преодоление которых жидкость затрачивает энергию. В результате полная удельная энергия жидкости в сечении 1-1 будет больше полной удельной энергии в сечении 2-2 на величину потерянной энергии (рис.10). 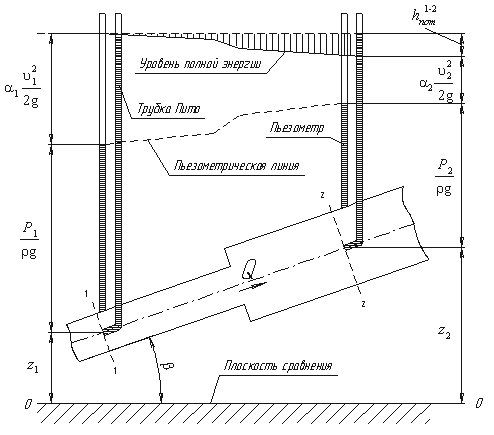 Рис.10. Схема к выводу уравнения Бернулли для реальной жидкости Уравнение Бернулли для реальной жидкости будет иметь вид: Из рис.10 видно, что по мере движения жидкости от сечения 1-1 до сечения 2-2 потерянный напор все время увеличивается (потерянный напор выделен вертикальной штриховкой). Таким образом, уровень первоначальной энергии, которой обладает жидкость в первом сечении, для второго сечения будет складываться из четырех составляющих: геометрической высоты, пьезометрической высоты, скоростной высоты и потерянного напора между сечениями 1-1 и 2-2. Кроме этого в уравнении появились еще два коэффициента α1 и α2, которые называются коэффициентами Кориолиса и зависят от режима течения жидкости ( α = 2 для ламинарного режима, α = 1 для турбулентного режима ). 2. Напишите уравнение Бернулли для элементарной струйки идеальной жидкости и для потока реальной жидкости. Объясните его физический смысл и дайте геометрическую интерпретацию. Ответ Уравнения приведены в ответе на первый вопрос. С физической точки зрения уравнение Бернулли есть выражение закона сохранения энергии для движущейся жидкости. Уравнению Бернулли можно дать наглядное геометрическое истолкование. Для этого снова рассмотрим отдельные члены суммы Имеем: г – геометрическая высота данной частицы жидкости над условной плоскостью сравнения; Таким образом, с геометрической точки зрения уравнение Бернулли в любом сечении элементарной струйки идеальной жидкости представляет собой сумму трех высот: геометрической, пьезометрической и скоростной, которая остается неизменной. График уравнения Бернулли для элементарной струйки идеальной жидкости представлен на рис. 11. 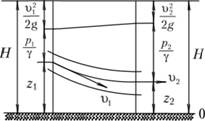 Рис. 11. График уравнения Бернулли Если сечение струйки увеличивается, то скорость падает, а давление возрастает, т.е. энергия, сохраняясь в целом, переходит из одного вида в другой (кинетическая энергия переходит в потенциальную и наоборот). |