Лекция 2. Основные комбинаторные конфигурации
 Скачать 69.98 Kb. Скачать 69.98 Kb.
|
|
ЛЕКЦИЯ 2 ТЕМА: ОСНОВНЫЕ КОМБИНАТОРНЫЕ КОНФИГУРАЦИИ Понятие комбинаторики Комбинаторика – раздел математики, посвященный решению задач выбора и расположения элементов конечного дискретного множества в соответствии с заданными правилами. Каждое такое правило определяет способ построения некоторой конструкции из элементов исходного множества, называемой комбинаторной конфигурацией. Основные правила комбинаторики Пусть B – конечное множество, состоящее из n элементов. Тогда элемент b, который принадлежит множеству B, может быть выбран n способами. Основными правилами комбинаторики являются правило суммы и правило произведения. 1. Правило суммы. Если элемент x может быть выбран n способами, а элемент y - m способами, то выбор "либо x, либо y" будет осуществлен n+m способами. 2. Правило произведения. Если элемент x может быть выбран n способами и после каждого из таких выборов элемент y может быть выбран m способами, то выбор упорядоченной пары (x, y) будет осуществлен nm способами. Правила суммы и произведения справедливы для любого числа элементов. Пример. Бросают два игральных кубика с шестью гранями каждый. Сколькими способами они могут упасть так, что либо на каждой грани выпадет четное число очков, либо на каждой грани выпадет нечетное число очков? Решение. Пусть A - число способов выпадения четного числа очков на каждой грани; В - число способов выпадения нечетного числа очков на каждой грани; D - число способов выпадения на каждой грани либо четного, либо нечетного количества очков. Тогда по правилу суммы искомое D=A+B. На первом кубике четное число очков может выпасть тремя способами, на втором тоже тремя. Тогда по правилу произведения A=33=9. Аналогично B=33=9. Следовательно, D=9+9=18. Комбинаторные конфигурации Набор элементов (a1, a2,…, ar ), составленный из элементов множества A= { a1… an}, называется выборкой объема r из n элементов, или (n, r) – выборкой. Выборка называется упорядоченной, если порядок следования элементов в ней существенен. Если порядок элементов в выборке несущественен, то выборка называется неупорядоченной. Упорядоченная (n, r) - выборка, в которой элементы могут повторяться, называется (n, r) - размещением с повторениями. Если элементы упорядоченной (n, r) - выборки попарно различны, то она называется (n, r) - размещением без повторений. (n, n) - размещения без повторений называются n – перестановками или перестановками из n элементов. Неупорядоченная (n, r) - выборка, в которой элементы могут повторяться, называется (n, r) - сочетанием с повторениями. Неупорядоченная (n, r) выборка, элементы которой не повторяются, называется (n, r) - сочетанием без повторений. Пример. Рассмотрим множество A={1, 2, 3} и определим его выборки. Размещения с повторениями: (1,1), (1, 2), (1,3), (2,1), (2,2), (2,3),(3,1),(3,2),(3, 3). Размещения без повторений: (1,2), (1,3), (2,1), (2,3), (3, 1), (3, 2). Сочетания с повторениями: (1, 1), (2, 2), (3,3), (1,2), (1,3), (2,3). Сочетания без повторений: (1,2), (2,3), (3,1). Перестановки: (1,2,3), (3,2,1), (3,1,2), (1,3,2), (2,3,1), (2,1,3). Обозначим число (n,r) - размещений без повторений через 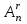 , число (n,r) - размещений с повторениями - , число (n,r) - размещений с повторениями - 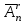 , число (n,r) - сочетаний с повторениями , число (n,r) - сочетаний с повторениями 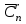 , число (n,r) - размещений без повторений , число (n,r) - размещений без повторений 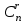 , число перестановок из n элементов Pn. , число перестановок из n элементов Pn. 1. Число (n, r) - размещений с повторениями определяется по следующей формуле: 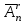 = nr. = nr.Действительно, каждое (n, r) - размещение с повторениями – это упорядоченная последовательность длины r. Каждый член последовательности может быть выбран n способами, следовательно, выбор r элементов может быть осуществлен nr способами. Пример. Сколькими способами из букв а, б, в, г, д можно составить слово из 3-х букв, если буквы могут повторяться? Решение: Количество способов - это число размещений с повторениями из 5 по 3, и оно равно 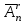 = 53 =125. = 53 =125.2. Число (n, r) размещений без повторений определяется следующим образом: 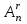 = =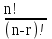 . . Действительно, каждое (n, r) - размещение без повторений – упорядоченная последовательность длины r. Первый элемент этой последовательности может быть выбран n способами, второй - (n-1) способом, третий - (n-2) способами и.т.д. Следовательно, число способов выбора r элементов определится в виде: 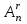 =n(n-1)(n-2)…(n-r+1)= =n(n-1)(n-2)…(n-r+1)= 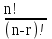 . . Пример. Сколькими способами из пяти цифр 1, 2, 3, 4, 5 можно составить трехзначное число, чтобы цифры не повторялись? Решение. Число способов равно 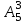 = =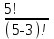 =20. =20. 3. Число перестановок из n элементов определяется следующим образом: Pn=n! Действительно, Pn= 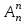 = n(n-1)(n-2)…1=n! = n(n-1)(n-2)…1=n!Пример. Сколькими способами можно расставить на полке 4 книги? Решение. Количество способов равно 4!=24. 4. Число (n, r) - сочетаний без повторений определяется следующим образом: 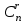 = = 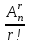 = = 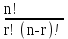 . .Данная формула следует из того, что каждому (n, r) - сочетанию без повторений соответствует r! размещений без повторений. Примеры. 1. Сколькими способами из группы студентов, состоящей из 20 человек, можно выбрать 3 делегатов на конференцию? Решение. В данном случае последовательность выбора роли не играет, поэтому искомое число способов равно количеству сочетаний без повторений из 20 по 3: 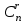 = =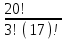 =1140. =1140. 2. В скольких случаях при угадывании 5 номеров из 36 будут правильно выбраны: a) три номера; б) четыре номера; в) пять номеров; г) не менее трех номеров; д) хотя бы один номер. Решение: a) три правильных номера из пяти могут быть выбраны 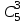 способами, оставшиеся два неправильных номера из 31 могут быть выбраны способами, оставшиеся два неправильных номера из 31 могут быть выбраны 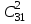 способами. По правилу произведения результат равен способами. По правилу произведения результат равен 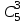 · ·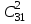 = 4650 . = 4650 . б) аналогично 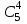 · ·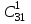 = 155. = 155.  в) все пять правильных номеров могут быть выбраны 1 способом. г) по правилу суммы результат будет равен 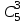 · ·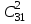 + +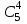 · ·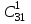 +1=4806. +1=4806. д) количество способов, при котором будет выбран хотя бы один правильный номер, можно определить, если из общего числа способов выбора 5 номеров из 36 вычесть число способов, при котором не будет выбран ни один правильный номер: 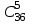 - -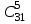 . . Для сочетаний без повторений выполняется следующее свойство: 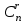 = =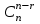 . .Действительно, 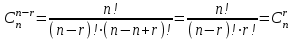 . .  5. Число (n, r) - сочетаний с повторениями определяется следующим образом: 5. Число (n, r) - сочетаний с повторениями определяется следующим образом: 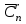 = = 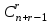 . . Пример. Сколько костей домино можно составить из цифр 0,1,2,3,4,5,6? Решение: Результат равен числу сочетаний с повторениями из 7 по 2: 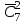 = = 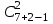 = =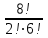 =28. =28. Урновые схемы В теории вероятностей рассматриваются комбинаторные схемы, связанные с выбором k шаров из урны с n шарами. При этом возможны следующие варианты: 1. Неупорядоченный выбор с возвращением k шаров из урны с n различными шарами. Число способов выбора в данном случае равно числу неупорядоченных k-выборок с повторением: N = 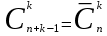 . . 2. Неупорядоченный выбор без возвращения k шаров из урны с n различными шарами. Число способов выбора равно количеству неупорядоченных k-выборок без повторения: 2. Неупорядоченный выбор без возвращения k шаров из урны с n различными шарами. Число способов выбора равно количеству неупорядоченных k-выборок без повторения:N = 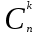 . .3. Упорядоченный выбор с возвращением k шаров из урны с n различными шарами. Число способов выбора равно количеству упорядоченных k-выборок с повторением: N = 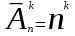 . .4. Упорядоченный выбор без возвращения k шаров из урны с n различными шарами. Число способов выбора определяется как количество упорядоченных k-выборок без повторения: N = 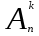 . .Пример. В урне содержатся 5 красных, 3 синих и 6 зеленых шаров. Из нее без возвращения выбирают 5 шаров, причем порядок выбора не существенен. Сколькими способами можно выбрать: 1) 3 красных и 2 синих шара; 2) все зеленые шары; 3) ни одного красного шара; 4) не менее 2 синих шаров; Решение: 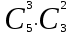 =15; =15; 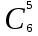 =6; =6;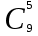 =126; =126;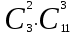 + +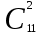 =530. =530. |
