тт_1. Основные понятия предмет и метод термодинамики
 Скачать 465.71 Kb. Скачать 465.71 Kb.
|
|
Т е х н и ч е с к а я т е р м о д и н а м и к а (по И.И. Новикову) Г л а в а 1 Основные понятия 1. предмет и метод термодинамики Термодинамика, наука об энергии и ее свойствах, изучает закономерности превращения энергии в физических, химических и других процессах, в том числе превращение тепла в работу в тепловых двигателях. Она основывается в основном на двух экспериментально установленных законах, получивших название первого и второго начал термодинамики. Первое начало термодинамики представляет собой приложение всеобщего закона природы – закона превращения и сохранения энергии – к тепловым явлениям. Второе начало термодинамики характеризует направление макроскопических процессов, протекающих в окружающей природе. Отражая особенности только этих процессов, второе начало термодинамики имеет более ограниченное значение по сравнению с первым. Задача термодинамики состоит в исследовании макроскопических свойств реальных тел в состоянии равновесия и процессов, происходящих с телами. В технической термодинамике ее законы применяют к процессам взаимного превращения тепла и работы. Основная задача технической термодинамики заключается в обосновании теории тепловых двигателей. 2. Термодинамические величины Тепло и работа Различные тела, взаимодействуя между собой, передают друг другу некоторое количество энергии; при этом соответственно изменяется состояние каждого из взаимодействующих тел. Передача энергии от одного тела к другому может осуществляться двумя способами. Первый способ передачи энергии хорошо известен из механики и состоит в совершении работы одним телом над другим. В этом случае увеличение энергии тела равно работе, произведенной над ним вторым телом. Работу будем обозначать – L. Принято считать, что работа, произведенная телом, положительна, а работа совершенная над телом (полученная им), отрицательна. Единицей работы в системе СИ является Джоуль (Дж). Передача энергии телу путем совершения над ним работы всегда связана с изменением внешних условий, в которых находится тело, и в частности с перемещением тела или отдельных его частей как целого. Второй способ передачи энергии не связан с совершением работы одним телом над другим и состоит в непосредственной передаче энергии от более нагретого тела к менее нагретому. Та часть энергии, которая передается телу от более нагретого тела непосредственно (в результате теплового контакта между ними), называется теплом, полученным телом. Количество тепла принято обозначать через Q. Тепло, полученное телом, считается положительным, а тепло, отданное телом, - отрицательным. Единицей количества тепла в системе СИ является Джоуль, в технической – килокалория (большая калория), которая практически равна количеству тепла, необходимого для нагревания 1 кг воды от 19,5 до 20.50С при нормальном атмосферном давлении. Количество работы и количество тепла являются мерой энергии, переданной телу в форме работы и в форме тепла. Количество работы, произведенной телом, и количество тепла, полученного телом, зависят от тех условий, в которых осуществляется изменение состояния тела, т.е. от характера процесса или от пути, по которому происходит переход тела из начального состояния в конечное. Термодинамическая система Объектом изучения термодинамики являются различные термодинамические системы. Термодинамической системой называют совокупность материальных тел, находящихся в механическом и тепловом взаимодействии как друг с другом, так и с окружающей (внешней) средой. Термодинамическую систему, которая не может обмениваться теплом с окружающей средой, называют теплоизолированной, или адиабатически изолированной, системой. Примером теплоизолированной системы является газ, находящийся в сосуде, стенки которого покрыты идеальной тепловой изоляцией, делающей невозможным теплообмен между заключенным в сосуд газом и окружающими телами. Такую идеальную теплоизолирующую оболочку называют адиабатической оболочкой. Всякую систему, заключенную в адиабатическую и абсолютно жесткую оболочку, которая делает невозможным как тепловое, так и механическое взаимодействие с окружающей средой, называют замкнутой, или изолированной. Система, имеющая во всех своих частях одинаковые свойства, называется однородной. Система, которая состоит из нескольких однородных, но различных частей, отделенных друг от друга поверхностями раздела, называется гетерогенной. Различные части, из которых состоит эта система, называются фазами. В соответствии с тремя видами агрегатного состояния вещества различают газообразную, жидкую и твердую (кристаллическую) фазы. Система, внутри которой поверхностей раздела не имеется и которая состоит из одной фазы, называется гомогенной. Макроскопические величины, характеризующие состояние системы в целом, называются термодинамическими параметрами. Из совокупности большого их числа особо должны быть выделены те параметры, при помощи которых описываются процессы взаимного превращения тепла и работы. Они получили название термических параметров. Главнейшими термическими параметрами являются температура, давление и объем (плотность) тела. Объем тела обозначается через V, давление – через р, темпера-тура: Цельсия – через tи абсолютная – через Т, причем Т = t0C+ 273,16K. Термодинамическое равновесие Если состояние термодинамической системы не меняется с течением времени (т.е. свойства системы в различные моменты времени одинаковы), то говорят, что система находится в термодинамическом равновесии, или просто в равновесии. В состоянии термодинамического равновесия передача тепла от одних частей системы к другим и механическое перемещение отдельных частей системы относительно друг друга отсутствует, т.е. имеет место тепловое и механическое равновесие. Состояние термодинамического равновесия неизолированной системы, взаимодействующей с окружающей средой, однозначно определяется заданием внешних условий – механических параметров и температуры окружающей среды. Любая система, находящаяся в неизменных внешних условиях, рано или поздно приходит в состояние термодинамического равновесия, каково бы ни было ее начальное состояние. Самопроизвольно выйти из состояния равновесия система не может (принцип самоненарушимости термодинамического равновесия). 3. Уравнение состояния В задачу термодинамики не входит установление аналитических зависимостей для конкретных свойств реальных тел (например, зависимости между давлением, объемом и температурой однородного тела, зависимости теплоемкости от температуры и т.д.). Эти зависимости устанавливаются или экспериментально, или, где это возможно, теоретическим путем, например на базе кинетической теории материи. Термодинамика обнаруживает, однако, ряд ограничений в свойствах тел и тем самым позволяет сформулировать некоторые общие закономерности в поведении реальных тел. Одна из этих общих закономерностей, относящаяся к однородным телам, состоит в следующем. Макроскопическое состояние всякого находящегося в равновесии однородного тела определяется всего лишь двумя независимыми параметрами. При этом предполагается, что никакого внешнего поля сил, действующих на тело, нет, так как в противном случае тело не могло бы иметь повсюду одинаковую плотность. Можно брать любую пару термических параметров: объем Vи температуру тела t или давление р и температуру Т и т.д. Все макроскопические или термодинамические величины, характеризующие равновесное состояние тела, могут быть представлены как функции этих двух параметров. Например, давление однородного тела р в состоянии равновесия может быть представлено в виде некоторой функции от температуры Т и объема тела (удельного v, молярного V или общего объема V). Уравнение р = f(t, V), (1.1) связывающее давление р, температуру tи объем V однородного тела в состоянии равновесия, называется термическим уравнением состояния тела. В трехмерном термодинамическом пространстве уравнение состояния тела характеризуется некоторой поверхностью, называемой термодинамической поверхностью данного тела. Уравнение состояния газов Форма уравнения состояния, т.е. вид функции р = f(t, V), определяется, как уже говорилось ранее, из опыта или устанавливается на основе кинетической теории материи. Идеальный газ. В идеальном газе силы межмолекулярного взаимодействия отсутствуют, а сами молекулы рассматриваются как материальные точки, лишенные пространственной протяженности. В этих случаях уравнение состояния имеет вид р = 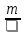 kNA103 kNA103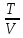 . (1.2) . (1.2)Произведение из константы Больцмана k на число молекул в 1 кгмоль вещества, равное числу Авогадро NA, умноженному на 103, называется универсальной газовой постоянной и обозначается R = kNA103. Числовое значение универсальной газовой постоянной равно: R = 6,02281026эргмольград = 848кгмкгмольград = 8,31441кДжкмольград. Величину R, равную отношению универсальной газовой постоянной R к молекулярной массе вещества, называют газовой постоянной для 1 кг данного вещества. Значения газовой постоянной Rдля ряда веществ приводятся в табл. 1. Если воспользоваться значением R, то уравнение (1.2) можно переписать в виде рV = mRT. (1.3) Уравнение (1.3) называется уравнением Клапейрона – Менделеева для идеального газа. Т а б л и ц а 1 Значение газовой постоянной для различных веществ
Если имеется смесь нескольких идеальных газов, то из-за отсутствия взаимодействия между молекулами каждый из газов ведет себя так, как будто других газов в смеси нет. Поэтому давление каждого из газов, составляющих смесь, будет равно тому давлению, которое имел бы этот газ, если бы он находился в том же количестве, объеме и при той же температуре, что и в смеси рi = miRi 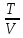 ..(1.4) ..(1.4)Давление рi называется парциальным давлением данного (i-го) газа; V – общий объем, занимаемый смесью газов, а Т – абсолютная температура смеси. Общее давление смеси идеальных газов равняется сумме парциальных давлений отдельных газов, составляющих смесь (закон Дальтона): рсм = 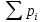 . (1.5) . (1.5)Реальный газ. Молекулы газов имеют конечные, хотя и весьма малые геометрические размеры и притягиваются друг к другу с силами, которые тем больше, чем меньше среднее расстояние между молекулами, т.е. чем меньше удельный объем газа. Сила, действующая на каждую из молекул, равна - 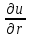 . При очень малых расстояниях между молекулами развиваются огромные силы отталкивания, в результате которых объем газа не может быть уменьшен ниже некоторого предела, равного для 1 кг величины b. . При очень малых расстояниях между молекулами развиваются огромные силы отталкивания, в результате которых объем газа не может быть уменьшен ниже некоторого предела, равного для 1 кг величины b.Из-за взаимодействия молекул свойства реальных газов отклоняются от идеальных; поэтому уравнение Клапейрона – Менделеева применимо к реальным газам лишь при большом разрежении, или, что то же самое, малой плотности последних. Силы взаимного притяжения препятствуют разлетанию молекул газа и действуют в том же направлении, что и внешнее давление р, удерживающее газ в определенном объеме. В результате действия этих сил возникает так называемое внутреннее, или молекулярное давление рмол: рмол = 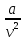 , ,где a– некоторый коэффициент. Уравнение состояния реального газа с учетом сил, действующих между молекулами, для 1 кг газа имеет следующий вид: (р + 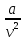 )(v – b) = RT. (1.6) )(v – b) = RT. (1.6)Величины a и b могут рассматриваться в первом приближении как некоторые константы, зависящие от природы вещества. Они вычисляются по формулам, связанным с критическими параметрами вещества a = 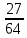 R2 R2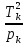 ; b = ; b = 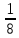 R R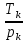 , (1.7) , (1.7)где рk – критическое давление данного вещества, Тk – его критическая температура. Критические температура и давление имеют простой физический смысл: взаимные превращения жидкой и газообразной фаз, в частности сжижение газа, возможны лишь при условии ttk , ppk . Критические давление, температура и объем представляют собой значения этих параметров в критической точке вещества, определяемой условиями равенству нулю при постоянной температуре первой и второй производной от (р, v). Критические параметры являются важнейшими термодинамическими характеристиками вещества, выражающими эффект действия молекулярных сил в обобщенной количественной форме. Уравнение (1.6) называется уравнением Ван-дер-Ваальса для реального газа. Это уравнение более точно, чем уравнение Клапейрона – Менделеева, но и оно является приближенным и применяется лишь в ограниченной области состояний. С целью усовершенствования уравнения Ван-дер-Ваальса и повышения его точности были предложены различные поправки к нему, в результате чего получен ряд новых уравнений. Некоторые из них использовались в определенной области состояний для составления таблиц термодинамических свойств веществ. Развитие кинетической теории материи привело в последние годы к установлению общего уравнения состояния реальных газов Рv = RT[1 - 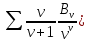 . (1.8) . (1.8)В этом уравнении коэффициенты Вv при степенях v в правой части уравнения, называемые вириальными коэффициентами, выражаются через потенциальную энергию и взаимодействия двух молекул данного газа и температуру Т и вычисляются, если известна функциональная зависимость u(r) от расстояния rмежду молекулами. Уравнение Ван-дер-Ваальса является частным случаем этого общего уравнения состояния, которое получается из него, когда пренебрегают всеми членами правой части уравнения (1.6), содержащими v во второй степени и выше, при невысокой плотности тела. Уравнение (1.8) почти не пригодно для практического использования, так как для обеспечения требующейся точности нужно сохранять в правой части большое количество членов, что придает ему весьма громоздкий вид. Кроме того, вычисление вириальных коэффициентов не во всех случаях осуществимо, так как точное выражение потенциальной энергии u(r) взаимодействия двух молекул для многих веществ неизвестно. Поэтому при расчете термодинамических свойств различных веществ и при составлении таблиц (или диаграмм) основываются обычно на экспериментальных данных, которые используют или непосредственно, или для получения эмпирических формул, на основе которых и производят все расчеты. |
