тт_1. Основные понятия предмет и метод термодинамики
 Скачать 465.71 Kb. Скачать 465.71 Kb.
|
|
Термодинамическое подобие Вместо переменных v, p, Tвведем новые переменные = 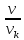 , = , = 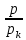 , = , = 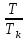 и назовем их соответственно приведенными объемом, давлением и температурой. Тогда, воспользовавшись выражением (1.8) для а и b, уравнение Ван-дер-Ваальса легко преобразовать к следующему виду: и назовем их соответственно приведенными объемом, давлением и температурой. Тогда, воспользовавшись выражением (1.8) для а и b, уравнение Ван-дер-Ваальса легко преобразовать к следующему виду:( + 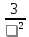 )(3 - 1) = 8. (1.9) )(3 - 1) = 8. (1.9)Уравнение (1.9) называется приведенным уравнением состояния Ван-дер-Ваальса. В это уравнение входят безразмерные параметры , , и числовые коэффициенты. Других величин, характеризующих данное вещество, в уравнении нет. Из этого следует, что приведенное уравнение одинаково для различных веществ, если они удовлетворяют уравнению Ван-дер-Ваальса. Состояния двух или нескольких веществ, в которых они имеют одинаковые приведенные параметры , , , называются соответственными состояниями. Если вещества удовлетворяют одному и тому же приведенному уравнению состояния и имеют одинаковые два из трех приведенных параметров , , , то и третий приведенный параметр у них будет одинаков, т.е. вещества находятся в соответственных состояниях. Это утверждение носит название закона соответственных состояний. Вещества, подчиняющиеся закону соответственных состояний и удовлетворяющие одному и тому же приведенному уравнению состояния, называются термодинамически подобными веществами. Критерием термодинамического подобия различных веществ является принадлежность этих веществ к одному и тому же классу химических соединений и равенство их критических коэффициентов, т.е. отношения RTkpkvk. Закон соответственных состояний не должен рассматриваться как следствие уравнения Ван-дер-Ваальса. Любое уравнение состояния, справедливое для всех или только для нескольких веществ, в котором, кроме универсальных постоянных (например, R, NA, k), содержатся лишь две индивидуальные константы, характеризующие природу вещества и изменяющиеся при переходе от одного вещества к другому, может быть преобразовано в приведенное уравнение состояния = f(, ). Это уравнение, будучи применимым ко всем рассматриваемым веществам, является математическим выражением закона соответственных состояний для данной группы веществ. Закон соответственных состояний относится не только к зависимости между параметрами ,, , но и распространяется на другие термодинамические величины. В частности, этот закон справедлив для состояний фазового равновесия жидкой и паровой фаз, поэтому для термодинамически подобных веществ кривая фазового равновесия в приведенных координатах должна иметь одинаковый вид. С другой стороны, закон соответственных состояний может быть применен к разнообразным процессам превращения механической энергии в тепло и передачи тепла от одного тела к другому. Во всех этих процессах термодинамически подобные вещества будут вести себя одинаково и удовлетворять одним и тем же уравнениям. 4. Термодинамический процесс Если изменяются внешние условия, в которых находится термодинамическая система, не изолированная от окружающей среды, то будет изменяться и состояние системы. Поэтому термодинамические параметры, характеризующие состояние системы, в разные моменты времени будут иметь различные значения. Последовательность изменений состояния системы образует термодинамический процесс. Всякий процесс изменения состояния тела представляет собой отклонение от состояния равновесия. Нарушение равновесия приводит к возникновению внутри тела процессов, противодействующих отклонению от состояния равновесия. Этими внутренними процессами, компенсирующими нарушение равновесия и восстанавливающими его, являются элементарные процессы обмена энергией при столкновении молекул. Процесс, протекающий настолько медленно (квазистатически), что в системе в каждый момент времени успевает установиться практически равновесное состояние, представляет собой квазиравновесный процесс. Степень приближения этого процесса к строго равновесному будет тем больше, чем меньше скорость изменения состояния системы. В пределе мы имеем бесконечно медленный процесс, который является вполне равновесным процессом и представляет собой совокупность состояний равновесия, последовательно проходимых системой. Если состояние системы в каждый момент процесса не является состоянием равновесия, то такой процесс изменения состояния называется неравновесным. В этом состоянии параметры системы вообще внешними условиями однозначно не определяются. Поэтому для характеристики неравновесного состояния, кроме внешних условий, нужно задавать еще один или несколько внутренних параметров. Особенности характера каждого из процессов изменения состояния тела определяются теми конкретными физическими условиями, в которых протекает данный процесс. Простейшими из них являются: изотермический, изобарический, изохорический, адиабатический процесс, когда тело помещено в теплоизолирующую оболочку, не допускающую теплообмена между телом и окружающей средой. В общем виде термодинамический процесс характеризуется условием Х = соnst, где Х – один из внешних или внутренних параметров системы или их некоторая функция. Среди термодинамических процессов особый интерес представляют замкнутые, или круговые процессы, при которых система, пройдя через ряд последовательных состояний, возвращается к исходному или к начальному состоянию. Круговой процесс называют также циклом. Равновесные процессы изменения тела допускают непосредственное графическое изображение. В любой момент времени термические параметры тела имеют вполне определенные значения. Благодаря этому каждое из состояний тела в равновесном процессе может быть изображено в термодинамическом пространстве точкой с соответствующими координатами в данный момент времени. Совокупность точек образует линию, которая зависит от закона изменения состояния тела. Неравновесные процессы графически изобразить в виде линии нельзя. 5. Аналитическое выражение работы и теплоты процесса Работа процесса Если бесконечно малое расширение системы происходит во внешней среде, находящейся повсюду под одним и тем же давлением р, то увеличение объема системы V на величину dV сопровождается элементарной работой dL = pdV, которая совершается системой над окружающей средой. Эта работа называется работой изменения объема. При равновесном процессе давление внешней среды рравно давлению тела р (р = р), поэтому выражение для dLв этом случае имеет вид dL = рdV. Выражение для работы L, совершаемой системой при конечном, а не бесконечно малом изменении ее объема от V1 до V2 будет иметь вид: L = 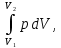 (1.10) (1.10)где интеграл берется по пути перехода системы в процессе 1-2. При равновесном процессе работу L, совершаемую системой, можно выразить так: L = 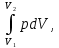 Работа зависит от пути, по которому система из состояния 1 переходит в состояние 2, т.е. она является функцией процесса, а не состояния. Это ясно видно, например, из выражения для работы равновесного процесса. Давление р согласно уравнению (1) зависит не только от объема Vтела, но и от его температуры t. Поэтому при переходе из одного и того же начального состояния 1 в одно и то же конечное состояние 2 давление р в промежуточных точках будет иметь разное значение в зависимости от величины температуры, которая изменяется в разных процессах по-разному; следовательно, и работа процесса Lбудет различной. 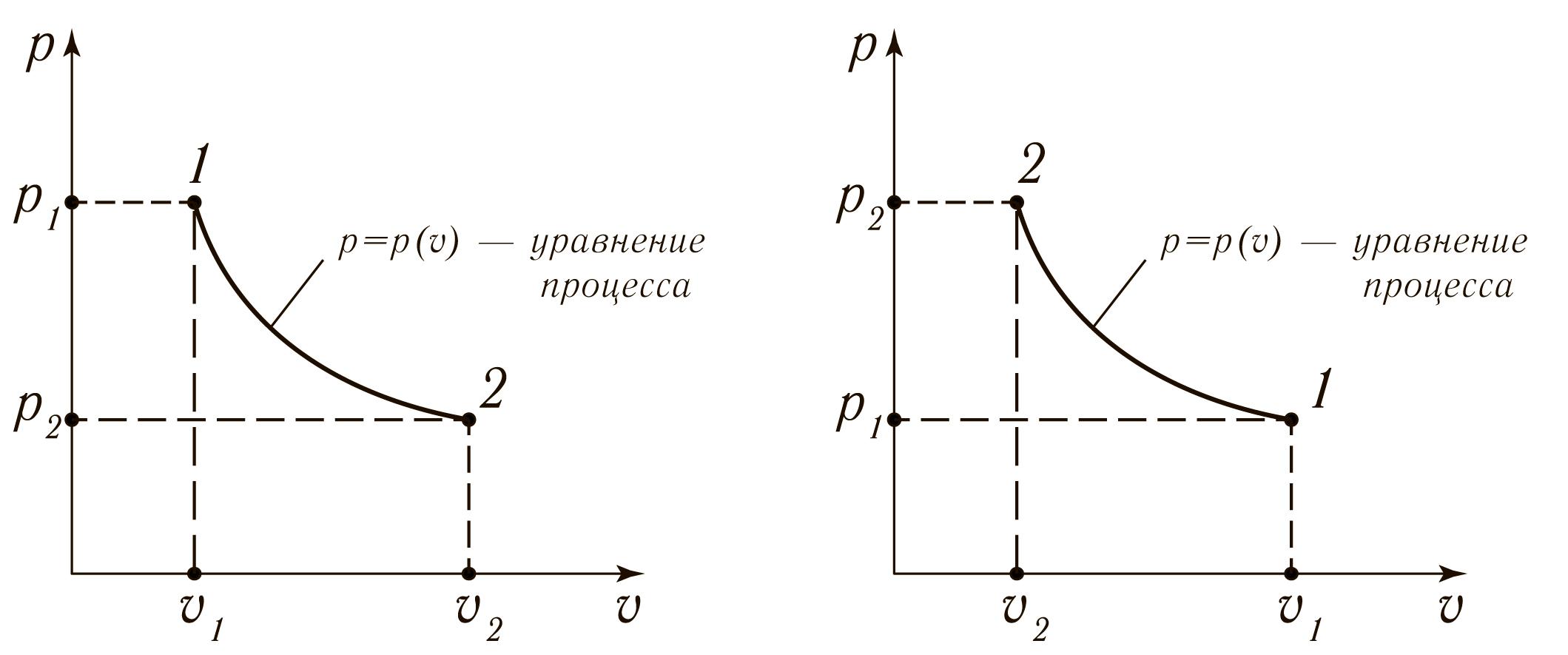 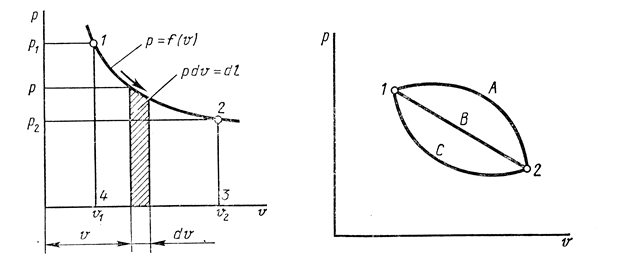 Рис. 7а. Работа расширения и сжатия Работу, совершаемую системой против внешних сил при увеличении объема, называют работой расширения, а работу, совершаемую внешними силами над системой при уменьшении объема системы, называют работой сжатия. Работа расширения имеет положительный знак, а работа сжатия – отрицательный. Работу системы, отнесенную к 1 кг массы вещества, называют удельной работой. Необходимо помнить, что работа, совершаемая системой в процессе изменения ее состояния, не равна нулю только в том случае, когда в результате процесса происходит перемещение тел, внешних по отношению к системе. При расширении тела в пустоту (в вакуум), когда никакого перемещения внешних тел не происходит, работа равняется нулю, поскольку при расширении в пустоту на границах тела и внешней среды давление р равно нулю. Работа, совершаемая системой, не всегда сводится только к работе изменения объема и поэтому не всегда выражается формулой (1.10). Например, если находящуюся в сосуде жидкость приводят в движение мешалкой, вращаемой извне, то работа, производимая внешним источником над жидкостью, имеет конечное значение, численно равное приращению кинетической энергии, в то время как работа изменения объема жидкости равна нулю. В самом общем случае работа L, производимая системой, равна сумме работы изменения объема и работы Lv, не связанной с изменением объема V системы L = 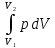 + Lv. + Lv.Вычислим полезную внешнюю работу, которая производится системой над некоторым внешним объектом при изменении состояния системы. Пусть рассматриваемая система представляет собой газ, находящийся в цилиндре под поршнем (рис. 8). Допустим, что 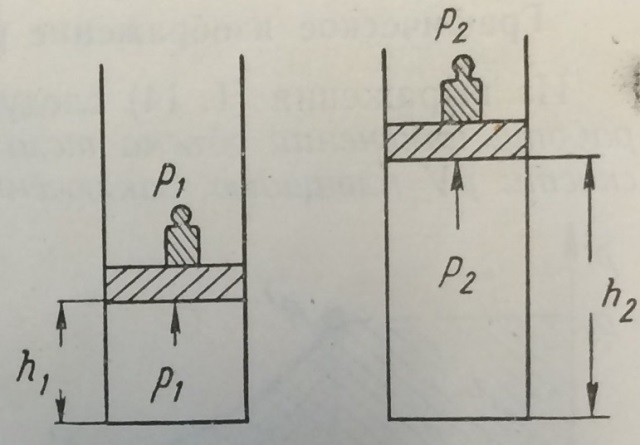 Рис. 8. Простейшая термодинамическая система произошло расширение газа от объема V1 до объема V2 V1; при этом поршень с грузом переместился с высоты h1 до высоты h2 h1. В результате расширения газ совершил работу L, а потенциальная энергия груза увеличилась на величину P2h2 – P1h1, равную p2V2 - p1V1 (поскольку hΩ = V). Разность между работой, совершенной газом, и приращением потенциальной энергии и есть та полезная работа L , которая произведена в результате данного процесса над внешним объектом: L = 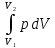 + Lv – (р2V2 - p1V1). (1.11) + Lv – (р2V2 - p1V1). (1.11)Так как 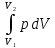 = - = - 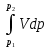 + p2V2 - p1V1, то полезная внешняя работа + p2V2 - p1V1, то полезная внешняя работаL= - 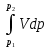 + Lv. (1.12) + Lv. (1.12)Величина p2V2 - p1V1 называется работой проталкивания. Здесь каждое из слагаемых представляет собой работу, которую надо произвести, чтобы ввести тело объемом V во внешнюю среду, находящуюся под давлением р. Графическое изображение работы равновесного процесса Из выражения (1.10) следует, что при равновесном процессе работа изменения объема тела L графически изображается на плоскости рV площадью, заключенной между кривой процесса и осью объемов ОV. Полезная внешняя работа L , есть площадь, заключенная между кривой процесса и осью давлений Ор. 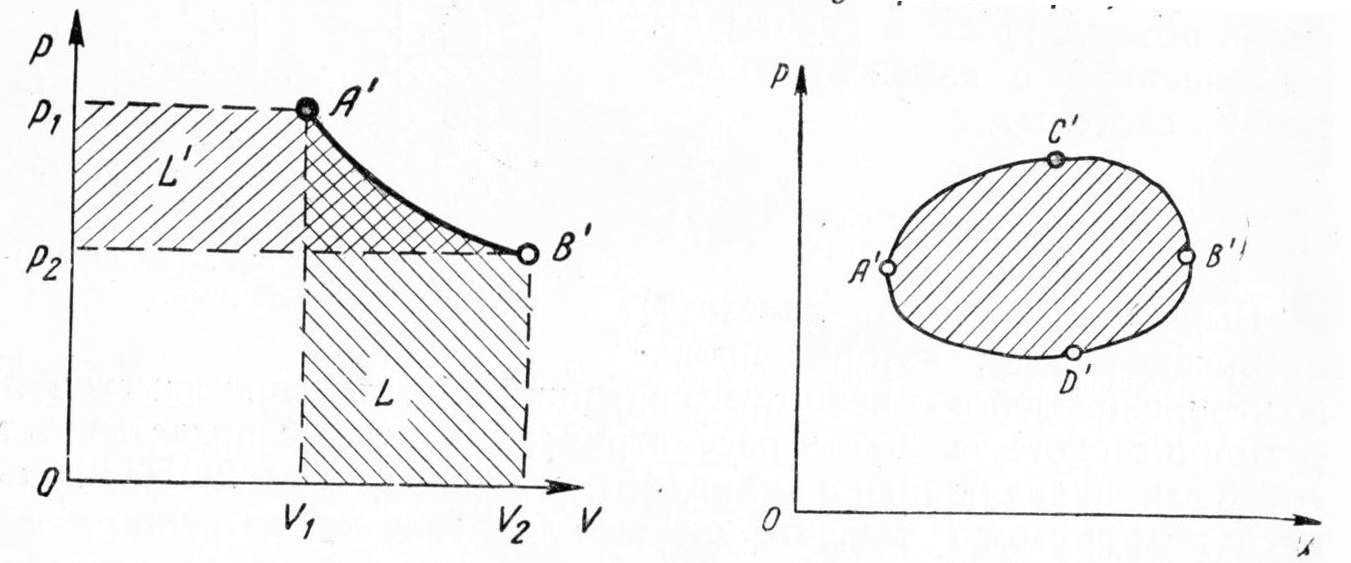 Рис. 8. Графическое изображение Рис.9. Графическое изображение работы равновесного процесса работы кругового процесса (цикла) Если тело совершает круговой процесс (цикл), изображаемый на плоскости рVзамкнутой кривой, то работа L, произведенная телом за один цикл, будет равна площади, ограниченной линией процесса (площади цикла). Если круговой процесс осуществляется по ходу движения часовой стрелки, работа будет положительной, а если против – отрицательной. Полезная внешняя работа L , произведенная телом в течение одного цикла, также выражается площадью цикла. Таким образом, L = L. Теплота процесса. Теплоемкость Наряду с совершением работы любой термодинамический процесс сопровождается подводом (или отводом) тепла к телу от окружающей среды. Сообщение телу тепла приводит к изменению его температуры, зависящему от внешних условий, в которых происходит изменение состояния тела, т.е. от характера процесса. Отношение количества тепла dQ, полученного телом при бесконечно малом изменении его состояния, к происшедшему в результате этого изменения температуры тела dt(dT) называется теплоемкостью тела Сх в данном процессе Сх = ( 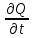 )х . (1.13) )х . (1.13)Теплоемкость численно равна количеству тепла, которое нужно сообщить телу, чтобы при данных условиях изменить его температуру на 1 градус. Теплоемкость Сх зависит от того, в каких условиях протекает процесс нагревания (или охлаждения) тела. На эту зависимость в уравнении (1.13) указывает индекс Х у частной производной, означающей, что процесс изменения температуры системы происходит вполне определенным и равновесным образом. Теплоемкость измеряется обычно в системе СИ ДжК, в технических единицах в килокалориях на градус Цельсия. Так как по уравнению (1.13) dQ = Cxdt, то общее количество тепла Q, полученного телом в данном процессе изменения состояния тела, определится выражением Q = 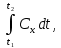 (1.14) (1.14)Где интеграл берется по пути процесса (по кривой, уравнение которой есть Х = соnst) от начального состояния 1 до конечного состояния 2. Из этого следует, что количество тепла Q есть функция процесса, а не состояния тела. В термодинамике особое значение имеет теплоемкость при постоянном объеме и при постоянном давлении СV =( 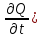 V ; Cp = V ; Cp = 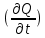 p . (1.15) p . (1.15)Уравнения (1.13) – (1.15) определяют величину теплоемкости при данных значениях параметров состояния T, Vи t, p. Эти значения С называют истинными теплоемкостями. Истинные теплоемкости являются функциями термических параметров тела. Для однородного тела истинные теплоемкости – это функции любых двух из трех параметров. Кроме истинных теплоемкостей, в технической термодинамике рассматривают еще так называемые средние теплоемкости 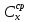 . Средняя теплоемкость данного процесса в интервале температур от t1 до t2 определяется следующим уравнением: . Средняя теплоемкость данного процесса в интервале температур от t1 до t2 определяется следующим уравнением: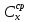 = = 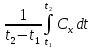 . (1.16) . (1.16) 6. Процессы обратимые и необратимые Обратимым процессом называется процесс, который может происходить как в прямом, так и в противоположном направлении и притом так, что при обратном процессе возвращаясь в исходное состояние, система проходит все те же состояния, что и при прямом, но в обратном порядке. Процессы, не удовлетворяющие этому условию, называются необратимыми. При таком процессе система не может быть возвращена в исходное состояние без дополнительного внешнего воздействия. При обратимом процессе система может вернуться в начальное состояние без дополнительного внешнего воздействия, а изолированная система – без всякого внешнего воздействия. Отсюда видно, что мерой необратимости процесса может служить величина дополнительного внешнего воздействия, например, работы, которое необходимо, чтобы возвратить тело в начальное состояние, или величина конечных изменений, остающихся во внешней среде после возвращения тела в начальное состояние. Если тело не находится в равновесии, то всякий процесс изменения состояния тела будет необратим. Например, неравновесный процесс изменения объема тела, в котором давление тела и давление окружающей среды различны, является процессом необратимым, поскольку работы, произведенной в результате процесса, будет не достаточно для обратного возвращения тела в начальное состояние. К этим процессам относится расширение тел в пустоту, расширение и сжатие при трении, отсутствие теплового равновесия и т.д. Следовательно, всякий неравновесный процесс изменения состояния тела всегда необратим. Необратимые процессы отличаются степенью необратимостью; в одних процессах она может быть больше, в других – меньше. В некоторых необратимых процессах состояние тела в каждой точке процесса сравнительно мало отличается от равновесного и характеризуется определенными значениями термодинамических параметров аналогично тому, как это имеет место в равновесных процессах. Такие процессы называются внешне необратимыми. Примером внешне необратимого процесса является изменение состояния тела при теплообмене с телом более высокой температуры. Несмотря на необратимый, вследствие конечной разности температур, характер теплообмена, состояния тел, обменивающихся теплом, мало отличаются от равновесного и могут рассматриваться в каждой точке процесса как состояния равновесия. Таким образом, с большой степенью приближения можно считать внешне необратимые процессы внутренне равновесными. ПРИЛОЖЕНИЕ Таблица 2 |
