студент. Лекция 16(1). Основные свойства непрерывных функций
 Скачать 74.13 Kb. Скачать 74.13 Kb.
|
|
Лекция №16 Тема: Основные свойства непрерывных функций. Производная. Теорема об устойчивости знака непрерывной функции. Первая теорема Больцано-Коши. Вторая теорема Больцано-Коши. Ограниченность непрерывных функции на отрезке. Первая теорема Вейерштрасса. Теорема о достижении функцией своих точных граней. Равномерная непрерывность. Теорема Кантора. Понятие обратной функции. Производная. Геометрический и механический смысл. Основные свойства непрерывных функций. Теорема(об устойчивости знака непрерывной функции). Пусть функция  непрерывна в точке а, причем непрерывна в точке а, причем 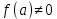 . Тогда существует такая . Тогда существует такая 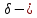 окрестность точки а, что для всех окрестность точки а, что для всех 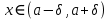 функция функция  имеет тот же знак, что и имеет тот же знак, что и 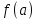 . .Доказательство. Пусть для определенности 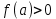 . Тогда согласно определению непрерывности функции в точке, для любого . Тогда согласно определению непрерывности функции в точке, для любого 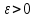 можно найти такое можно найти такое 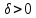 , что для всех x, удовлетворяющих неравенству , что для всех x, удовлетворяющих неравенству 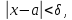 выполняется неравенство выполняется неравенство 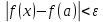 или, что тоже самое, или, что тоже самое,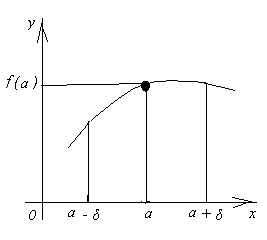 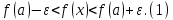 Возьмем 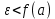 , тогда из левого неравенства в (1) получаем, что , тогда из левого неравенства в (1) получаем, что 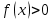 для всех xиз -окрестности точки a. В случае для всех xиз -окрестности точки a. В случае 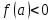 рассмотрим функцию рассмотрим функцию 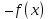 . Так как она положительна в точке a, то для нее существует . Так как она положительна в точке a, то для нее существует 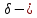 окрестность точки a, в которой окрестность точки a, в которой 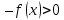 , а значит , а значит 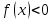 . .ч.т.д. Первая теорема Больцано-Коши. Пусть функция  непрерывна на отрезке непрерывна на отрезке 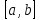 и на его концах принимает значение разных знаков. Тогда внутри и на его концах принимает значение разных знаков. Тогда внутри 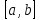 существует точка существует точка 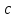 , в которой , в которой 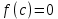 . .Доказательство. Пусть для определенности 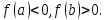 Разделим отрезок Разделим отрезок 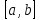 пополам. Если значение функции в середине отрезка равно нулю, то теорема доказана. пополам. Если значение функции в середине отрезка равно нулю, то теорема доказана.В противном случае из двух половин отрезка возьмем тот сегмент, на концах которого  принимает значение разных знаков. Обозначим его принимает значение разных знаков. Обозначим его 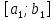 . .Р 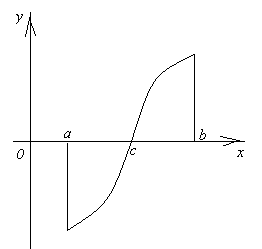 азделим его пополам и повторим процедуру, обозначив через азделим его пополам и повторим процедуру, обозначив через 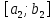 отрезок вдвое меньше, на концах которого отрезок вдвое меньше, на концах которого  принимает значения разных знаков. принимает значения разных знаков.Продолжая этот процесс либо на каком – то m-м шаге значение  в середине отрезка в середине отрезка 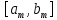 равно нулю и теорема доказана, либо мы получим последовательность вложенных отрезков равно нулю и теорема доказана, либо мы получим последовательность вложенных отрезков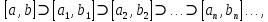 причем 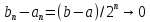 при при 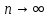 . .По теореме о вложенных отрезках существует точка c принадлежащая всем отрезкам. Покажем, что 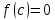 . Действительно, если . Действительно, если 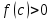 , то по теореме об устойчивости знака непрерывной функции существует некоторая окрестность точки c, в которой , то по теореме об устойчивости знака непрерывной функции существует некоторая окрестность точки c, в которой 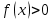 . При достаточно большом . При достаточно большом 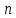 в эту окрестность попадает отрезок в эту окрестность попадает отрезок 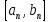 , в котором будет , в котором будет 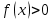 . Это противоречит тому, что на концах всех вложенных отрезков функция . Это противоречит тому, что на концах всех вложенных отрезков функция 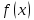 принимает значения разных знаков. Аналогично доказывается, что значение принимает значения разных знаков. Аналогично доказывается, что значение 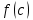 не может быть отрицательным. Следовательно, не может быть отрицательным. Следовательно, 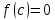 , причем , причем 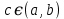 . .ч.т.д. Вторая теорема Больцано-Коши. Пусть функция 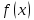 непрерывна на отрезке непрерывна на отрезке 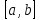 , причем , причем 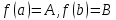 . Пусть C- любое число заключенное между A и B. Тогда на отрезке . Пусть C- любое число заключенное между A и B. Тогда на отрезке 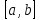 найдется точка c, что найдется точка c, что 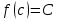 . .Доказательство. Пусть 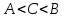 . Рассмотрим вспомогательную функцию . Рассмотрим вспомогательную функцию 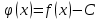 . Эта функция непрерывна на . Эта функция непрерывна на 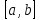 и принимает на концах этого отрезка значения разных знаков и принимает на концах этого отрезка значения разных знаков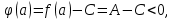 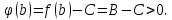 По первой теореме Больцано – Коши существует такая точка 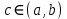 , что , что 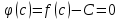 . Откуда . Откуда 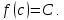 ч.т.д. Смысл теоремы заключается в утверждении, что непрерывная функция при переходе от одного значения к другому принимает все промежуточные значения. Ограниченность непрерывных функций на отрезке. Функция  называется ограниченной на отрезке [a, b],если называется ограниченной на отрезке [a, b],если существует такое число М, что для всех 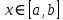 выполняется неравенство выполняется неравенство 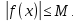 Первая теорема Вейерштрасса. Если функция  определена и непрерывна на отрезке определена и непрерывна на отрезке 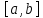 , то она ограничена на этом отрезке. , то она ограничена на этом отрезке.Доказательство. От противного, то есть предположим, что функция  не ограничена на отрезке не ограничена на отрезке 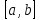 . Разделим отрезок . Разделим отрезок 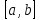 пополам. По крайней мере на одном из двух полученных отрезков функция пополам. По крайней мере на одном из двух полученных отрезков функция  неограничена. Обозначим этот отрезок через неограничена. Обозначим этот отрезок через 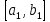 . Разделим его пополам и ту половину, на которой . Разделим его пополам и ту половину, на которой  не ограничена, обозначим через не ограничена, обозначим через 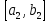 и т.д. продолжая это процесс неограниченно, получим последовательность вложенных отрезков, на каждом из которых функция и т.д. продолжая это процесс неограниченно, получим последовательность вложенных отрезков, на каждом из которых функция  не ограничена, причем длина отрезков стремится к нулю: не ограничена, причем длина отрезков стремится к нулю: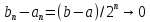 при при 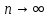 . .Следовательно, существует точка 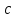 , принадлежащая всем отрезкам. Функция , принадлежащая всем отрезкам. Функция  определена и непрерывна в точке определена и непрерывна в точке 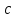 и ограничена в некоторой ее окрестности. Однако при достаточно большом и ограничена в некоторой ее окрестности. Однако при достаточно большом 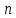 в эту окрестность попадает отрезок в эту окрестность попадает отрезок 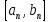 , на котором , на котором  не ограничена. Это противоречие снимает предположение о неограниченности функции не ограничена. Это противоречие снимает предположение о неограниченности функции  на отрезке на отрезке 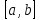 . . ч.т.д. Теорема(достижение функцией своих точных граней). Если функция  непрерывна на отрезке [a,b], то она достигает на этом отрезке своих точных граней, то есть найдутся такие точки непрерывна на отрезке [a,b], то она достигает на этом отрезке своих точных граней, то есть найдутся такие точки 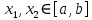 , что , что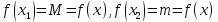 . .Доказательство.Так как функция  непрерывна на отрезке непрерывна на отрезке 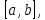 то она ограничена на этом отрезке. Отсюда заключаем, что существует точная верхняя и точная нижняя грани функции то она ограничена на этом отрезке. Отсюда заключаем, что существует точная верхняя и точная нижняя грани функции  на отрезке на отрезке 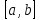 . .Допустим, что функция  не принимает ни в одной точке не принимает ни в одной точке 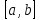 значения, равного M. Тогда для всех значения, равного M. Тогда для всех 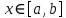 должно быть должно быть 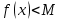 . .Рассмотрим вспомогательную функцию 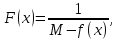 которая положительна и непрерывна на 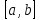 . Тогда по предыдущей теореме функция . Тогда по предыдущей теореме функция 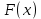 ограничена, то есть существует такое ограничена, то есть существует такое 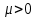 , что на отрезке , что на отрезке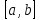 для всех x для всех x 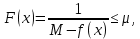 откуда откуда 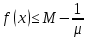 . .Последнее неравенство противоречит тому, что число M является точной верхней гранью функции  на отрезке на отрезке 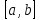 (так как (так как 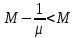 ). Это противоречие доказывает, что существует точка ). Это противоречие доказывает, что существует точка 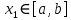 , в которой , в которой 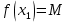 . .Достижение функцией  на отрезке на отрезке 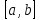 своей точной нижней грани доказывается аналогично. своей точной нижней грани доказывается аналогично. ч.т.д. Заметим, что для непрерывной на отрезке функции ее точную верхнюю грань называют максимальным значением, а точную нижнюю грань – минимальным значением функции на этом отрезке. Разность между максимальным и минимальным значением непрерывной на отрезке 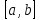 функции функции  называется колебанием ее на этом отрезке. называется колебанием ее на этом отрезке.Равномерная непрерывность функции. Функция  называется равномерно – непрерывнойна промежутке X, если для любого называется равномерно – непрерывнойна промежутке X, если для любого 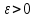 найдется такое найдется такое 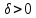 , что для любых двух точек , что для любых двух точек 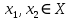 , удовлетворяющих неравенству , удовлетворяющих неравенству 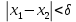 выполняется неравенство выполняется неравенство 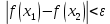 . .Для равномерно – непрерывной функции величина 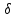 зависит только от зависит только от 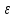 и является общей для всего промежутка X. и является общей для всего промежутка X.Из определения следует, что если функция равномерно – непрерывна на X, то она является непрерывной на этом промежутке и по заданному 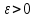 можно найти такое можно найти такое 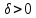 , что промежуток X может быть разбит на составные промежутки длиной меньше , что промежуток X может быть разбит на составные промежутки длиной меньше 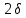 , на каждом из которых колебание функции составляет меньше, чем 2 , на каждом из которых колебание функции составляет меньше, чем 2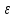 . .Теорема Кантора. Если функция  непрерывна на отрезке [a,b], то она и равномерно непрерывна на нем. непрерывна на отрезке [a,b], то она и равномерно непрерывна на нем.Понятие обратной функции. Говорят, что функция  не убывает (не взрастает)на множестве не убывает (не взрастает)на множестве 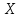 , если для любых , если для любых 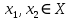 , таких, что , таких, что 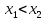 , справедливо неравенство , справедливо неравенство 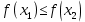 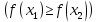 . .Неубывающие и невозрастающие функции называются монотонными функциями. Если 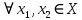 таким, что таким, что 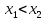 , выполняется неравенство , выполняется неравенство 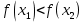 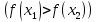 , то функция , то функция  называется возрастающей(убывающей) на множестве называется возрастающей(убывающей) на множестве 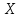 . Такие функции называются также строго монотонными. . Такие функции называются также строго монотонными.Например, функция 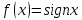 неубывающая на всей числовой прямой. Функция неубывающая на всей числовой прямой. Функция 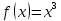 возрастающая на всей числовой прямой. возрастающая на всей числовой прямой.Функция 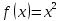 является убывающей на промежутке является убывающей на промежутке 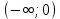 и возрастающей на и возрастающей на 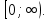 Пусть на множестве X задана функция 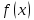 , причем , причем 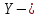 множество ее значений то есть задано множество пар чисел множество ее значений то есть задано множество пар чисел 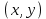 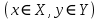 , в котором каждое число , в котором каждое число 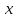 входит лишь в одну пару, а каждое число входит лишь в одну пару, а каждое число 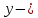 по крайней мере в одну пару. Если в каждой паре этого множества поменять местами числа по крайней мере в одну пару. Если в каждой паре этого множества поменять местами числа 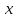 и и 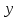 , то получим множество пар чисел , то получим множество пар чисел 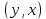 , которое называется обратной функцией к функции , которое называется обратной функцией к функции 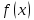 . Обозначим обратную функцию символом . Обозначим обратную функцию символом 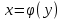 . .Теорема. Пусть функция 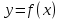 определена, строго монотонна и непрерывна на некотором промежутке определена, строго монотонна и непрерывна на некотором промежутке 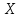 и пусть и пусть 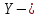 множество ее значений. Тогда на множестве множество ее значений. Тогда на множестве 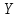 обратная функция обратная функция 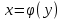 однозначна, строго монотонна и непрерывна. однозначна, строго монотонна и непрерывна.Производная. Геометрический и механический смысл производной. Пусть функция  определена на некотором промежутке определена на некотором промежутке 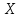 . Придадим значению аргумента в точке . Придадим значению аргумента в точке 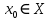 приращение приращение 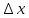 так, чтобы точка так, чтобы точка 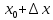 также принадлежала X. Тогда соответствующее приращение функции также принадлежала X. Тогда соответствующее приращение функции  составит составит 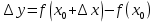 . .Производной функции  в точке в точке 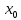 называется предел отношения приращения функции в этой точке к приращению аргумента при называется предел отношения приращения функции в этой точке к приращению аргумента при  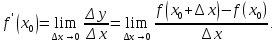 Если функция  имеет производную в каждой точке множества X, то производная имеет производную в каждой точке множества X, то производная 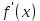 также является функцией аргумента x, определенной на X. также является функцией аргумента x, определенной на X.Выясним геометрический смысл производной. Пусть точка M на кривой 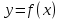 соответствует значению аргумента соответствует значению аргумента 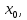 а точка N – значению аргумента а точка N – значению аргумента 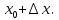 Из определения касательной следует, что для ее существования в точке Из определения касательной следует, что для ее существования в точке 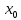 нужно, чтобы существовал предел нужно, чтобы существовал предел 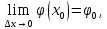 который равен углу наклона касательной к оси 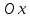 . . 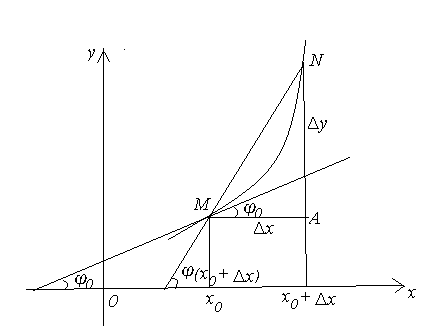 Из треугольника MNA следует, что Из треугольника MNA следует, что 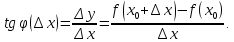 Если производная функции  в точке 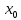 существует, то, согласно определению производной существует, то, согласно определению производной 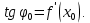 Таким образом, производная Таким образом, производная 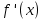 равна угловому коэффициенту(тангенсу угла наклона к положительному направлению оси равна угловому коэффициенту(тангенсу угла наклона к положительному направлению оси 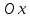 ) касательнойк графику функции ) касательнойк графику функции 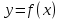 в точке в точке 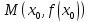 . При этом угол наклона определяется как . При этом угол наклона определяется как 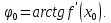 Определим механический смысл производной. Пусть функция 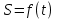 описывает закон движения материальной точки по прямой, как зависимость пути описывает закон движения материальной точки по прямой, как зависимость пути 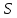 от времени от времени 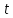 . Тогда разность . Тогда разность 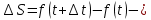 это путь, пройденный за интервал времени это путь, пройденный за интервал времени 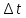 , а отношение , а отношение 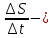 средняя скорость за время средняя скорость за время 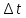 . Тогда . Тогда 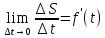 определяет мгновенную скорость точки в момент времени 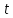 как производную от пути по времени. как производную от пути по времени.В определенном смысле производную функции 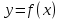 можно также трактовать как скорость изменения функции: чем больше величина можно также трактовать как скорость изменения функции: чем больше величина 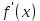 , тем больше угол наклона касательной к кривой, тем круче график , тем больше угол наклона касательной к кривой, тем круче график  и быстрее растет функция. и быстрее растет функция.Вопросы для самоконтроля Теорема об устойчивости знака непрерывной функции. Первая теорема Больцано – Коши. Вторая теорема Больцано – Коши. Дайте определение функции ограниченной на отрезке. Первая теорема Вейерштрасса. Теорема о достижение функцией своих точных граней. Дайте определение равномерно непрерывной на промежутке функции. Монотонные функции. Обратная функция. Дайте определение производной функции в точке. Геометрический смысл производной. Механический смысл производной.  |
