опорный конспект гидростатика. Основные теоретические сведения Давление. Закон Паскаля. Гидростатическое давление
 Скачать 45.42 Kb. Скачать 45.42 Kb.
|
|
Основные теоретические сведения Давление. Закон Паскаля. Гидростатическое давление Основным отличием жидкостей от твердых (упругих) тел является способность легко изменять свою форму. Части жидкости могут свободно сдвигаться, перемещаясь друг относительно друга. Поэтому жидкость принимает форму сосуда, в который она налита. В жидкость, как и в газообразную среду, можно погружать твердые тела. В отличие от газов жидкости практически несжимаемы. На тело, погруженное в жидкость или газ, действуют силы, распределенные по поверхности тела. Для описания таких распределенных сил в гидростатике вводится новая физическая величина – давление. Давление определяется как отношение модуля силы F, действующей перпендикулярно поверхности, к площади S этой поверхности: Если же сила направлена под некоторым углом к перпендикуляру к площадке, то создаваемое этой силой давление находится по формуле: В системе СИ давление измеряется в паскалях (Па): 1 Па = 1 Н/м2. Часто используются внесистемные единицы: нормальное атмосферное давление (атм) и давление одного миллиметра ртутного столба (мм.рт.ст.): 1 атм = 101325 Па = 760 мм.рт.ст. Закон Паскаля: давление, оказываемое на жидкость (или, к слову, газ), передается в любую точку этой жидкости без изменений и во всех направлениях. Давление жидкости на дно или боковые стенки сосуда зависит от высоты столба жидкости над той точкой в которой измеряется давление. Гидростатическое давление столба жидкости рассчитывается по формуле: Обратите внимание, что оказываемое давление никоим образом не зависит от формы сосуда, а зависит только от рода жидкости (т.е. её плотности) и от высоты столба этой жидкости. Такое же давление на глубине h в соответствии с законом Паскаля жидкость оказывает и на боковые стенки сосуда. Итак, если в задаче по гидростатике идет речь о давлении столба жидкости на боковую грань в некоторой конкретной точке, то такое давление находится по предыдущей формуле, где h – расстояние от этой точки до поверхности жидкости. Но иногда в задачах по гидростатике необходимо рассчитать среднее давление на всю боковую поверхность сосуда. В таком случае применим формулу: В этом случае, h – это общая высота столба жидкости в сосуде. Если жидкость находится в цилиндре под поршнем, то действуя на поршень некоторой внешней силой F, можно создавать в жидкости дополнительное давление p0 = F/S, где: S – площадь поршня. Таким образом, полное давление в жидкости на глубине h можно записать в виде: Если поршень убрать, то давление на поверхность жидкости будет равно атмосферному давлению. Если мы погружаемся в воду, то давление на некоторой глубине тоже будет состоять из двух давлений – давления атмосферы и давления столба воды (которое определяется глубиной погружения). Сообщающиеся сосуды Сообщающимися называют сосуды, имеющие между собой канал, заполненный жидкостью. Наблюдения показывают, что в сообщающихся сосудах любой формы однородная жидкость всегда устанавливается на одном уровне. задачи на сообщающиеся сосуды очень распространены в гидростатике. Иначе ведут себя разнородные жидкости даже в одинаковых по форме и размерам сообщающихся сосудах. Дело в том, что в сообщающихся сосудах должно устанавливаться одинаковое давление на одной и той же высоте во всех частях сосуда. Но если жидкости различные, то и высота столбов этих жидкостей должна быть различной, чтобы создать одинаковое давление. Поэтому, разнородные жидкости в сообщающихся сосудах могут и не устанавливаться на одном уровне. Алгоритм решения задач по гидростатике на сообщающиеся сосуды: Сделать рисунок. Выбрать горизонтальный уровень, ниже которого во всех сосудах находится одинаковая жидкость. Если такого уровня нет, то, естественно, за нулевой уровень выбираем дно сосудов. Записать давления относительно этого уровня во всех сосудах и приравнять. При необходимости использовать свойство несжимаемости жидкости (объем жидкости, вытекающей из одного сосуда, равен объему жидкости, втекающей в другой сосуд). Решить математически полученную систему уравнений. Гидравлический пресс Если оба вертикально расположенных цилиндра сообщающихся сосудов закрыть поршнями, то с помощью внешних сил, приложенных к поршням, в жидкости можно создать большое давление p, во много раз превышающее гидростатическое давление ρgh в любой точке системы. Тогда можно считать, что во всей системе устанавливается одинаковое давление p (согласно закону Паскаля). Если поршни имеют разные площади S1 и S2, то на них со стороны жидкости действуют разные силы F1 = pS1 и F2 = pS2. Такие же по модулю, но противоположно направленные внешние силы должны быть приложены к поршням для удержания системы в равновесии. Таким образом, для гидравлического пресса имеем формулу: 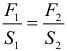 Это соотношение вытекает из равенства давлений и выполняется только в идеальном гидравлическом прессе, т.е. таком в котором нет трения. Если S2 >> S1, то и F2 >> F1. Устройства в которых выполняются эти условия называют гидравлическими прессами (машинами, домкратами). Они позволяют получить значительный выигрыш в силе. Если поршень в узком цилиндре переместить вниз под действием внешней силы F1 на расстояние h1, то поршень в широком цилиндре переместится на расстояние h2, которое может быть найдено из соотношения: Данное соотношение вытекает из равенства объемов и выполняется в любом гидравлическом прессе. Это выражение получается потому, что при перемещении поршня перемещаются одинаковые объемы жидкости, то есть сколько жидкости ушло из одного цилиндра столько же пришло во второй, или V1 = V2. Таким образом, выигрыш в силе обязательно сопровождается таким же проигрышем в расстоянии. При этом произведение силы на расстояние остается неизменным: Последняя формула вытекает из равенства работ и выполняется только для идеальных машин, в которых не действуют силы трения. Таким образом, в гидравлическом прессе всё происходит в полном соответствии с «золотым правилом механики»: во сколько раз мы выигрываем в силе, во столько же раз мы проигрываем в расстоянии. При этом ни одна машина не может дать выигрыша в работе. Так как гидравлический пресс является механизмом, то его работу можно характеризовать КПД (коэффициентом полезного действия). КПД гидравлического пресса в задачах по гидростатике рассчитывается по следующей формуле: 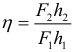 где: Апол = F2h2 – полезная работа (работа по подъему груза), Азатр = F1h1 – затраченная работа. В большинстве задач КПД гидравлического пресса принимают за 100%. КПД рассчитывается в том случае, если речь идет о неидеальном гидравлическом прессе. Еще раз подчеркнем, что для неидеального гидравлического пресса выполняется только соотношение, вытекающее из равенства объемов вытесненной жидкости, а также для таких прессов рассчитывается КПД. Остальные соотношения из этого раздела выполняются только для идеального гидравлического пресса. Закон Архимеда. Вес тела в жидкости Из–за разности давлений в жидкости на разных уровнях возникает выталкивающая или Архимедова сила, которая вычисляется по формуле: где: V – объем вытесненной телом жидкости, или же объем погружённой в жидкость части тела, ρ – плотность жидкости в которую погружено тело, и следовательно, ρV – масса вытесненной жидкости. Архимедова сила, действующая на погруженное в жидкость (или газ) тело, равна весу жидкости (или газа), вытесненной телом. Это утверждение, называемое законом Архимеда, справедливо для тел любой формы. При этом вес тела (т.е. сила с которой тело действует на опору или подвес) погруженного в жидкость уменьшается. Если принять, что вес покоящегося тела в воздухе равен mg, а именно так мы и будем поступать в большинстве задач (хотя вообще говоря на тело в воздухе также действует очень маленькая сила Архимеда со стороны атмосферы, ведь тело погружено в газ из атмосферы), то для веса тела в жидкости можно легко вывести следующую важную формулу:  Эта формула может быть использована при решении большого количества задач. Ее можно запомнить. При помощи закона Архимеда осуществляется не только мореплавание, но и воздухоплавание. Из закона Архимеда вытекает, что если средняя плотность тела ρт больше плотности жидкости (или газа) ρ (или по–другому mg > FA), тело будет опускаться на дно. Если же ρт < ρ (или по–другому mg < FA), тело будет плавать на поверхности жидкости. Объем погруженной части тела будет таков, что вес вытесненной жидкости равен весу тела. Для подъема воздушного шара в воздухе его вес должен быть меньше веса вытесненного воздуха. Поэтому воздушные шары заполняют легкими газами (водородом, гелием) или нагретым воздухом. Плавание тел Если тело находится на поверхности жидкости (плавает), то на него действует всего две силы (Архимеда вверх и тяжести вниз), которые уравновешивают друг друга. Если тело погружено только в одну жидкость, то записав второй закон Ньютона для такого случая и выполнив простые математические операции можем получить следующее выражение связывающее объемы и плотности: 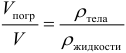 где: Vпогр – объем погруженной части тела, V – полный объем тела. При помощи этого соотношения легко решается большинство задач на плавание тел. |
