Курсовая Инвестиции. Курсовик инвестиции. Основной целью данной работы является рассмотрение методов, принципов, источников инвестиций на предприятиях

• Название: Основной целью данной работы является рассмотрение методов, принципов, источников инвестиций на предприятиях
• Анкор: Курсовая Инвестиции
• Дата: 24.06.2022
• Размер: 82.27 Kb.
• Имя файла: Курсовик инвестиции.docx
• Тип: Документы; #613808
• страница: 4 из 5

2. Методы оценки эффективности инвестиций

В основе процесса принятия управленческих решений инвестиционного характера лежат оценка и сравнение объема предполагаемых инвестиций и будущих денежных поступлений. Поскольку сравниваемые показатели относятся к различным моментам времени, ключевой проблемой здесь является проблема их сопоставимости. Относиться к ней можно по-разному в зависимости от существующих объективных и субъективных условий: темпа инфляции, размера инвестиций и генерируемых поступлений, горизонта прогнозирования, уровня квалификации аналитика и т. п.

Методы, используемые в анализе инвестиционной деятельности, можно подразделить на две группы: а) основанные на дисконтированных оценках; б) основанные на учетных оценках. Рассмотрим ключевые идеи, лежащие в основе этих методов.

2.1. Метод чистой теперешней стоимости

Этот метод основан на сопоставлении величины исходной инвестиции (IC) с общей суммой дисконтированных чистых денежных поступлений, генерируемых ею в течение прогнозируемого срока. Поскольку приток денежных средств распределен во времени, он дисконтируется с помощью коэффициента r, устанавливаемого аналитиком (инвестором) самостоятельно исходя из ежегодного процента возврата, который он хочет или может иметь на инвестируемый им капитал.

Допустим, делается прогноз, что инвестиция (IC) будет генерировать в течение n лет, годовые доходы в размере P₁, P₂, ..., Р_n. Общая накопленная величина дисконтированных доходов (PV) и чистый приведенный эффект (NPV) соответственно рассчитываются по формулам: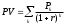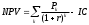

, .

Очевидно, что если: NPV > 0, то проект следует принять;

NPV < 0, то проект следует отвергнуть;

NPV = 0, то проект ни прибыльный, ни убыточный.
При прогнозировании доходов по годам необходимо по возможности учитывать все виды поступлений как производственного, так и непроизводственного характера, которые могут быть ассоциированы с данным проектом. Так, если по окончании периода реализации проекта планируется поступление средств в виде ликвидационной стоимости оборудования или высвобождения части оборотных средств, они должны быть учтены как доходы соответствующих периодов.

Если проект предполагает не разовую инвестицию, а последовательное инвестирование финансовых ресурсов в течение m лет, то формула для расчета NPV модифицируется следующим образом: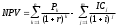
,
где i — прогнозируемый средний уровень инфляции.

Расчет с помощью приведенных формул вручную достаточно трудоемок, поэтому для удобства применения этого и других методов, основанных на дисконтированных оценках, разработаны специальные статистические таблицы, в которых табулированы значения сложных процентов, дисконтирующих множителей, дисконтированного значения денежной единицы и т. п. в зависимости от временного интервала и значения коэффициента дисконтирования.

Необходимо отметить, что показатель NPV отражает прогнозную оценку изменения экономического потенциала предприятия в случае принятия рассматриваемого проекта. Этот показатель аддитивен во временном аспекте, т. е. NPV различных проектов можно суммировать. Это очень важное свойство, выделяющее этот критерий из всех остальных и позволяющее использовать его в качестве основного при анализе оптимальности инвестиционного портфеля.

2.2. Метод внутренней ставки дохода

Под нормой рентабельности инвестиции (IRR) понимают значение коэффициента дисконтирования, при котором NPV проекта равен нулю:
IRR = r, при котором NPV = f(r) = 0.
Смысл расчета этого коэффициента при анализе эффективности планируемых инвестиций заключается в следующем: IRR показывает максимально допустимый относительный уровень расходов, которые могут быть ассоциированы с данным проектом. Например, если проект полностью финансируется за счет ссуды коммерческого банка, то значение IRR показывает верхнюю границу допустимого уровня банковской процентной ставки, превышение которого делает проект убыточным.

На практике любое предприятие финансирует свою деятельность, в том числе и инвестиционную, из различных источников. В качестве платы за пользование авансированными в деятельность предприятия финансовыми ресурсами оно уплачивает проценты, дивиденды, вознаграждения и т.п., т.е. несет некоторые обоснованные расходы на поддержание своего экономического потенциала. Показатель, характеризующий относительный уровень этих расходов, можно назвать "ценой" авансированного капитала (CC). Этот показатель отражает сложившийся на предприятии минимум возврата на вложенный в его деятельность капитал, его рентабельность и рассчитывается по формуле средней арифметической взвешенной.

Экономический смысл этого показателя заключается в следующем: предприятие может принимать любые решения инвестиционного характера, уровень рентабельности которых не ниже текущего значения показателя CC (или цены источника средств для данного проекта, если он имеет целевой источник). Именно с ним сравнивается показатель IRR, рассчитанный для конкретного проекта, при этом связь между ними такова.
Если: IRR > CC. то проект следует принять;

IRR < CC, то проект следует отвергнуть;

IRR = CC, то проект ни прибыльный, ни убыточный.
Практическое применение данного метода осложнено, если в распоряжении аналитика нет специализированного финансового калькулятора. В этом случае применяется метод последовательных итераций с использованием табулированных значений дисконтирующих множителей. Для этого с помощью таблиц выбираются два значения коэффициента дисконтирования r₁2 таким образом, чтобы в интервале (r₁,r₂) функция NPV=f(r) меняла свое значение с "+" на "-" или с "-" на "+". Далее применяют формулу

,

где r₁ — значение табулированного коэффициента дисконтирования, при котором f(r₁)>0 (f(r₁)<0);

r₂ — значение табулированного коэффициента дисконтирования, при котором f(r₂)<О (f(r₂)>0).
Точность вычислений обратно пропорциональна длине интервала (r₁,r₂), а наилучшая аппроксимация с использованием табулированных значений достигается в случае, когда длина интервала минимальна (равна 1%), т.е. r₁ и r₂ - ближайшие друг к другу значения коэффициента дисконтирования, удовлетворяющие условиям (в случае изменения знака функции с "+" на "-"):
r₁ — значение табулированного коэффициента дисконтирования, минимизирующее положительное значение показателя NPV, т.е. f(r₁)=min_r{f(r)>0};

r₂ — значение табулированного коэффициента дисконтирования, максимизирующее отрицательное значение показателя NPV, т.е. f(r₂)=max_r{f(r)<0}.
Путем взаимной замены коэффициентов r₁ и r₂ аналогичные условия выписываются для ситуации, когда функция меняет знак с "-" на "+".