Шшшш. калобок. Особая форма материи, существующая вокруг движущихся электрических зарядов токов
 Скачать 231.74 Kb. Скачать 231.74 Kb.
|
|
Магнитное поле – особая форма материи, существующая вокруг движущихся электрических зарядов – токов. Источниками магнитного поля являются постоянные магниты, проводники с током. Обнаружить магнитное поле можно по действию на магнитную стрелку, проводник с током и движущиеся заряженные частицы. Для исследования магнитного поля используют замкнутый плоский контур с током (рамку с током). Впервые поворот магнитной стрелки около проводника, по которому протекает ток, обнаружил в 1820 году Эрстед. Ампер наблюдал взаимодействие проводников, по которым протекал ток: если токи в проводниках текут в одном направлении, то проводники притягиваются, если токи в проводниках текут в противоположных направлениях, то они отталкиваются. Свойства магнитного поля: магнитное поле материально; источник и индикатор поля – электрический ток; магнитное поле является вихревым – его силовые линии (линии магнитной индукции) замкнутые; величина поля убывает с расстоянием от источника поля. Важно! Магнитное поле не является потенциальным. Его работа на замкнутой траектории может быть не равна нулю. Магнитным взаимодействием называют притяжение или отталкивание электрически нейтральных проводников при пропускании через них электрического тока. Магнитное взаимодействие движущихся электрических зарядов объясняется так: всякий движущийся электрический заряд создает в пространстве магнитное поле, которое действует на движущиеся заряженные частицы. Силовая характеристика магнитного поля – вектор магнитной индукции B⃗ . Модуль вектора магнитной индукции равен отношению максимального значения силы, действующей со стороны магнитного поля на проводник с током, к силе тока в проводнике I и его длине l: 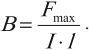 Обозначение – B⃗ , единица измерения в СИ – тесла (Тл). 1 Тл – это индукция такого магнитного поля, в котором на каждый метр длины проводника при силе тока 1 А действует максимальная сила 1 Н. Направление вектора магнитной индукции совпадает с направлением от южного полюса к северному полюсу магнитной стрелки (направление, которое указывает северный полюс магнитной стрелки), свободно установившейся в магнитном поле. Направление вектора магнитной индукции можно определить по правилу буравчика: если направление поступательного движения буравчика совпадает с направлением тока в проводнике, то направление вращения ручки буравчика совпадает с направлением вектора магнитной индукции. Для определения магнитной индукции нескольких полей используется принцип суперпозиции: магнитная индукция результирующего поля, созданного несколькими источниками, равна векторной сумме магнитных индукций полей, создаваемых каждым источником в отдельности: Поле, в каждой точке которого вектор магнитной индукции одинаков по величине и направлению, называется однородным. Наглядно магнитное поле изображают в виде магнитных линий или линий магнитной индукции. Линия магнитной индукции – это воображаемая линия, в любой точке которой вектор магнитной индукции направлен по касательной к ней. Свойства магнитных линий: магнитные линии непрерывны; магнитные линии замкнуты (т.е. в природе не существует магнитных зарядов, аналогичных электрическим зарядам); магнитные линии имеют направление, связанное с направлением тока. Густота расположения позволяет судить о величине поля: чем гуще расположены линии, тем сильнее поле. На плоский замкнутый контур с током, помещенный в однородное магнитное поле, действует момент сил M: где I – сила тока в проводнике, S – площадь поверхности, охватываемая контуром, B – модуль вектора магнитной индукции, α – угол между перпендикуляром к плоскости контура и вектором магнитной индукции. Тогда для модуля вектора магнитной индукции можно записать формулу: где максимальный момент сил соответствует углу α = 90°. В этом случае линии магнитной индукции лежат в плоскости рамки, и ее положение равновесия является неустойчивым. Устойчивым будет положение рамки с током в случае, когда плоскость рамки перпендикулярна линиям магнитной индукции. Содержание Взаимодействие магнитов Магнитное поле проводника с током Сила Ампера Сила Лоренца Основные формулы раздела «Магнитное поле» Взаимодействие магнитов Постоянные магниты – это тела, длительное время сохраняющие намагниченность, то есть создающие магнитное поле. Основное свойство магнитов: притягивать тела из железа или его сплавов (например стали). Магниты бывают естественные (из магнитного железняка) и искусственные, представляющие собой намагниченные железные полосы. Области магнита, где его магнитные свойства выражены наиболее сильно, называют полюсами. У магнита два полюса: северный N и южный S. Важно! Вне магнита магнитные линии выходят из северного полюса и входят в южный полюс. Разделить полюса магнита нельзя. Объяснил существование магнитного поля у постоянных магнитов Ампер. Согласно его гипотезе внутри молекул, из которых состоит магнит, циркулируют элементарные электрические токи. Если эти токи ориентированы определенным образом, то их действия складываются и тело проявляет магнитные свойства. Если эти токи расположены беспорядочно, то их действие взаимно компенсируется и тело не проявляет магнитных свойств. Магниты взаимодействуют: одноименные магнитные полюса отталкиваются, разноименные – притягиваются. Магнитное поле проводника с током Электрический ток, протекающий по проводнику с током, создает в окружающем его пространстве магнитное поле. Чем больше ток, проходящий по проводнику, тем сильнее возникающее вокруг него магнитное поле. Магнитные силовые линии этого поля располагаются по концентрическим окружностям, в центре которых находится проводник с током. Направление линий магнитного поля вокруг проводника с током всегда находится в строгом соответствии с направлением тока, проходящего по проводнику. Направление магнитных силовых линий можно определить по правилу буравчика: если поступательное движение буравчика (1) совпадает с направлением тока (2) в проводнике, то вращение его рукоятки укажет направление силовых линий (4) магнитного поля вокруг проводника. 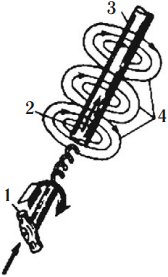 При изменении направления тока линии магнитного поля также изменяют свое направление. По мере удаления от проводника магнитные силовые линии располагаются реже. Следовательно, индукция магнитного поля уменьшается. Направление тока в проводнике принято изображать точкой, если ток идет к нам, и крестиком, если ток направлен от нас.  Для получения сильных магнитных полей при небольших токах обычно увеличивают число проводников с током и выполняют их в виде ряда витков; такое устройство называют катушкой. В проводнике, согнутом в виде витка, магнитные поля, образованные всеми участками этого проводника, будут внутри витка иметь одинаковое направление. Поэтому интенсивность магнитного поля внутри витка будет больше, чем вокруг прямолинейного проводника. При объединении витков в катушку магнитные поля, созданные отдельными витками, складываются. При этом концентрация силовых линий внутри катушки возрастает, т. е. магнитное поле внутри нее усиливается. Чем больше ток, проходящий через катушку, и чем больше в ней витков, тем сильнее создаваемое катушкой магнитное поле. Магнитное поле снаружи катушки также складывается из магнитных полей отдельных витков, однако магнитные силовые линии располагаются не так густо, вследствие чего интенсивность магнитного поля там не столь велика, как внутри катушки.  Магнитное поле катушки с током имеет такую же форму, как и поле прямолинейного постоянного магнита: силовые магнитные линии выходят из одного конца катушки и входят в другой ее конец. Поэтому катушка с током представляет собой искусственный электрический магнит. Обычно для усиления магнитного поля внутрь катушки вставляют стальной сердечник; такую катушку называют электромагнитом. Направление линий магнитной индукции катушки с током находят по правилу правой руки: если мысленно обхватить катушку с током ладонью правой руки так, чтобы четыре пальца указывали направление тока в ее витках, тогда большой палец укажет направление вектора магнитной индукции. Для определения направления линий магнитного поля, создаваемого витком или катушкой, можно использовать также правило буравчика: если вращать ручку буравчика по направлению тока в витке или катушке, то поступательное движение буравчика укажет направление вектора магнитной индукции. Электромагниты нашли чрезвычайно широкое применение в технике. Полярность электромагнита (направление магнитного поля) можно определить и с помощью правила правой руки. Сила Ампера Сила Ампера – сила, которая действует на проводник с током, находящийся в магнитном поле. Закон Ампера: на проводник c током силой I длиной l, помещенный в магнитное поле с индукцией B⃗ , действует сила, модуль которой равен: где α – угол между проводником с током и вектором магнитной индукции B⃗ . Направление силы Ампера определяют по правилу левой руки: если ладонь левой руки расположить так, чтобы перпендикулярная к проводнику составляющая вектора магнитной индукции B⊥ входила в ладонь, а четыре вытянутых пальца указывали направление тока в проводнике, то отогнутый на 90° большой палец покажет направление силы Ампера.  Сила Ампера не является центральной. Она направлена перпендикулярно линиям магнитной индукции. Сила Ампера широко используется. В технических устройствах создают магнитное поле с помощью проводников, по которым течет электрический ток. Электромагниты используют в электромеханическом реле для дистанционного выключения электрических цепей, магнитном подъемном кране, жестком диске компьютера, записывающей головке видеомагнитофона, в кинескопе телевизора, мониторе компьютера. В быту, на транспорте и в промышленности широко применяют электрические двигатели. Взаимодействие электромагнита с полем постоянного магнита позволило создать электроизмерительные приборы (амперметр, вольтметр). Простейшей моделью электродвигателя служит рамка с током, помещенная в магнитное поле постоянного магнита. В реальных электродвигателях вместо постоянных магнитов используют электромагниты, вместо рамки – обмотки с большим числом витков провода. Коэффициент полезного действия электродвигателя: где N – механическая мощность, развиваемая двигателем. Коэффициент полезного действия электродвигателя очень высок. Алгоритм решения задач о действии магнитного поля на проводники с током: сделать схематический чертеж, на котором указать проводник или контур с током и направление силовых линий поля; отметить углы между направлением поля и отдельными элементами контура; используя правило левой руки, определить направление силы Ампера, действующей на проводник с током или на каждый элемент контура, и показать эти силы на чертеже; указать все остальные силы, действующие на проводник или контур; записать формулы для остальных сил, упоминаемых в задаче. Выразить силы через величины, от которых они зависят. Если проводник находится в равновесии, то необходимо записать условие его равновесия (равенство нулю суммы сил и моментов сил); записать второй закон Ньютона в векторном виде и в проекциях; решить полученную систему уравнений относительно неизвестной величины; решение проверить. Сила Лоренца Сила Лоренца – сила, действующая на движущуюся заряженную частицу со стороны магнитного поля. Формула для нахождения силы Лоренца: где q – заряд частицы, v – скорость частицы, B – модуль вектора магнитной индукции, α – угол между вектором скорости частицы и вектором магнитной индукции. Направление силы Лоренца определяют по правилу левой руки: если ладонь левой руки расположить так, чтобы перпендикулярная к проводнику составляющая вектора магнитной индукции B⊥ входила в ладонь, а четыре вытянутых пальца указывали направление скорости положительно заряженной частицы, то отогнутый на 90° большой палец покажет направление силы Лоренца. 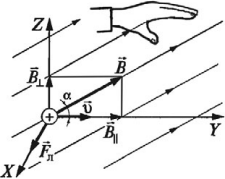 Если заряд частицы отрицательный, то направление силы изменяется на противоположное. Важно! Если вектор скорости сонаправлен с вектором магнитной индукции, то частица движется равномерно и прямолинейно. В однородном магнитном поле сила Лоренца искривляет траекторию движения частицы. Если вектор скорости перпендикулярен вектору магнитной индукции, то частица движется по окружности, радиус которой равен: где m – масса частицы, v – скорость частицы, B – модуль вектора магнитной индукции, q – заряд частицы. В этом случае сила Лоренца играет роль центростремительной и ее работа равна нулю. Период (частота) обращения частицы не зависит от радиуса окружности и скорости частицы. Формула для вычисления периода обращения частицы: 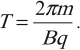 Угловая скорость движения заряженной частицы: Важно! Сила Лоренца не меняет кинетическую энергию частицы и модуль ее скорости. Под действием силы Лоренца изменяется направление скорости частицы. Если вектор скорости направлен под углом α (0° < α < 90°) к вектору магнитной индукции, то частица движется по винтовой линии. В этом случае вектор скорости частицы можно представить как сумму двух векторов скорости, один из которых, v⃗ 2, параллелен вектору B⃗ , а другой, v⃗ 1, – перпендикулярен ему. Вектор v⃗ 1 не меняется ни по модулю, ни по направлению. Вектор v⃗ 2 меняется по направлению. Сила Лоренца будет сообщать движущейся частице ускорение, перпендикулярное вектору скорости v⃗ 1. Частица будет двигаться по окружности. Период обращения частицы по окружности – T. Таким образом, на равномерное движение вдоль линии индукции будет накладываться движение по окружности в плоскости, перпендикулярной вектору B⃗ . Частица движется по винтовой линии с шагом h=v2T.  Важно! Если частица движется в электрическом и магнитном полях, то полная сила Лоренца равна: Особенности движения заряженной частицы в магнитном поле используются в масс-спектрометрах – устройствах для измерения масс заряженных частиц; ускорителях частиц; для термоизоляции плазмы в установках «Токамак». Алгоритм решения задач о действии магнитного (и электрического) поля на заряженные частицы: сделать чертеж, указать на нем силовые линии магнитного (и электрического) поля, нарисовать вектор начальной скорости частицы и отметить знак ее заряда; изобразить силы, действующие на заряженную частицу; определить вид траектории частицы; разложить силы, действующие на заряженную частицу, вдоль направления магнитного поля и по направлению, ему перпендикулярному; составить основное уравнение динамики материальной точки по каждому из направлений разложения сил; выразить силы через величины, от которых они зависят; решить полученную систему уравнений относительно неизвестной величины; решение проверить. По определению колебательный контур (или LC-контур) – это электрическая цепь, в которой происходят свободные электромагнитные колебания. Такой контур представляет собой электрическую цепь, состоящую из катушки индуктивностью L и конденсатора емкостью C. Соединены эти два элемента могут быть лишь двумя способами - последовательно и параллельно. Покажем на рисунке ниже изображение и схему простейшего колебательного контура. Давайте рассмотрим пример, когда сначала мы заряжаем конденсатор и замыкаем цепь. После этого в цепи начинает течь синусоидальный электрический ток. Конденсатор разряжается через катушку. В катушке при протекании через нее тока возникает ЭДС самоиндукции, направленная в сторону, противоположную току конденсатора. Разрядившись окончательно, конденсатор благодаря энергии ЭДС катушки, которая в этот момент будет максимальна, начнет заряжаться вновь, но только в обратной полярности. Колебания, которые происходят в контуре – свободные затухающие колебания. То есть без дополнительной подачи энергии колебания в любом реальном колебательном контуре рано или поздно прекратятся, как и любые колебания в природе. Это обусловлено тем, что контур состоит из реальных материалов (конденсатор, катушка, провода), обладающих таким свойством, как электрическое сопротивление, и потери энергии в реальном колебательном контуре неизбежны. В противном случае это нехитрое устройство могло бы стать вечным двигателем, существование которого, как известно, невозможно. Электромагнитные колебания в LC-контуре происходят с определенной частотой, которая называется резонансной Подробнее про резонанс – в нашей отдельной статье. Частоту колебаний можно менять, варьируя такие параметры контура, как емкость конденсатора C, индуктивность катушки L, сопротивление резистора R (для LCR-контура). Как рассчитать резонансную частоту колебательного контура? Очень просто! Приведем окончательную формулу: 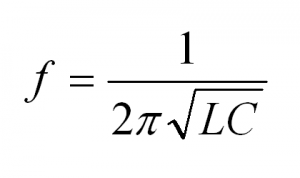 |
