Специальные главы математики, отчет номер 1. СГМ ОТЧЕТ 1. Осуществить дискретизацию сигнала и выполнить дискретное преобразование Фурье

• Название: Осуществить дискретизацию сигнала и выполнить дискретное преобразование Фурье
• Анкор: Специальные главы математики, отчет номер 1
• Дата: 16.05.2023
• Размер: 374.98 Kb.
• Имя файла: СГМ ОТЧЕТ 1.docx
• Тип: Документы; #1135709

Цель работы:

Осуществить дискретизацию сигнала и выполнить дискретное преобразование Фурье.

Продискретизировать исходный сигнал. Провести ДПФ по формуле и с помощью встроенных функций Mathcad, построить графики спектров и сделать сравнения.

Исследовать эффект «утечки бинов» спектра.

Выполнение работы:

1. 
   Задаем параметры сигнала G(t):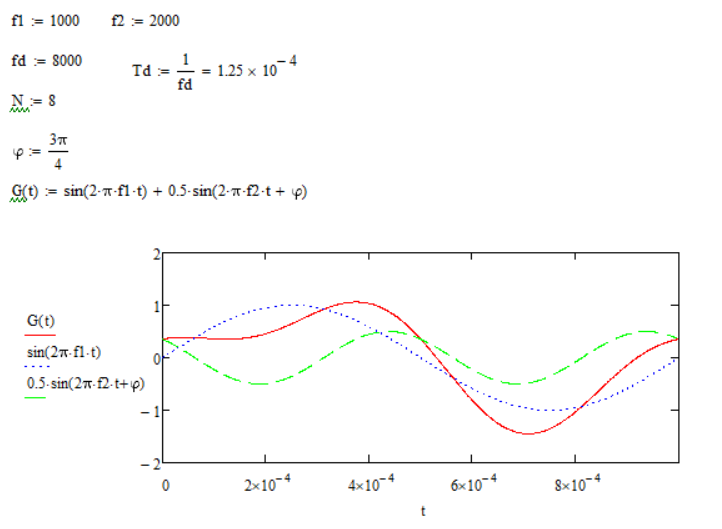
   

Рис. 1 – Исходные данные сигнала
Задаем функцию формирования отсчетов сигнала G(t):



Рис. 2 – Функция формирования отсчетов исходного сигнала
Далее записываем функцию ДПФ в тригонометрическом виде и выводим получившийся массив: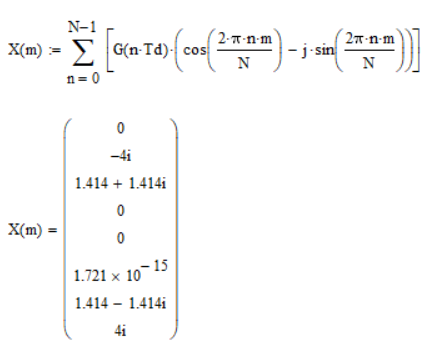



Рис. 3 – ДПФ и массив значений
Выведем графики модулей, фаз, действительной и мнимой частей ДПФ: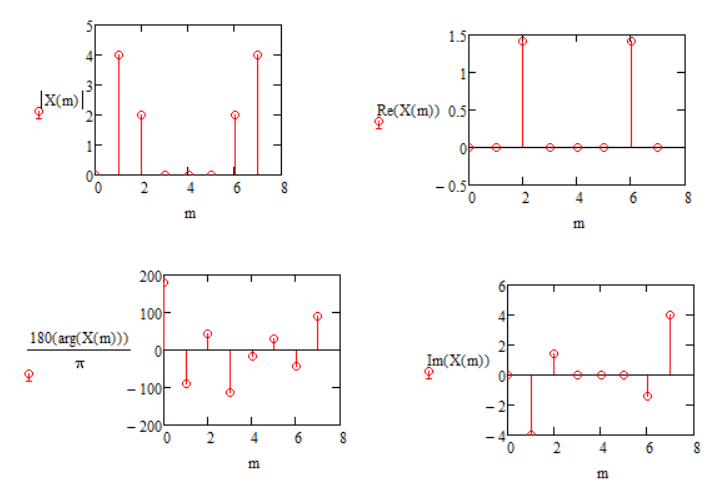



Рис. 4 – Графики модулей, фаз, мнимой и действительной частей
Действительная часть имеет четную симметрию, а мнимая нечетную.

Можно вычислять только половину отсчетов, а другую получать с учетом симметрии при помощи алгоритма БПФ (fft).

Сравниваем графики с теоретическими и накладываем дополнительное условие зануления элементов массива, меньших по модулю чем 10^-14 для графика фаз: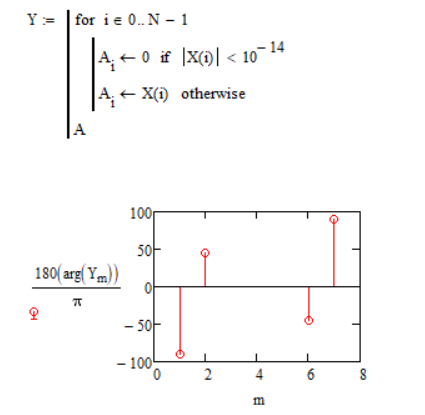



Рис. 5 – Вид графика фаз после изменения
Пишем формулу для ОДПФ и выводим массив значений, сравниваем с исходными:



Рис. 6 – ОДПФ, массивы ОДПФ и исходный
Реализуем ДПФ и ОДПФ с помощью встроенных функций: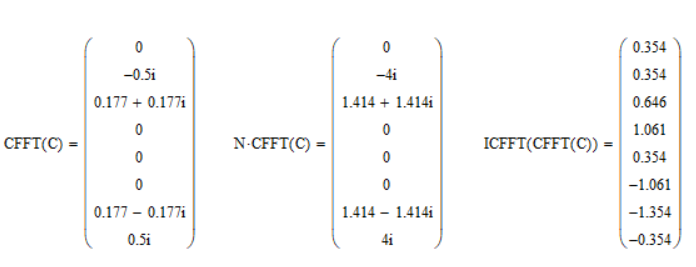



Рис. 7 – Реализация ДПФ и ОДПФ с помощью Mathcad
Домножение на количество отсчетов необходимо, так как во встроенной функции присутствует коэффициент 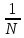. Данные полученные с помощью встроенных функций равны полученным по формулам. Использование функции значительно экономит время.

2. 
   Задаем новый сигнал с другими параметрами:
   

Рис. 8 – Исходные данные
Формируем массив отсчетов сигнала:



Рис. 9 – Массив отсчетов сигнала
Преобразуем с помощью функции ДПФ и выведем модули частотных составляющих: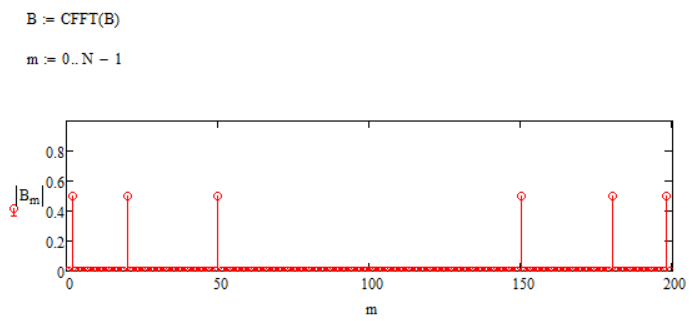



Рис. 10 – Спектр сигнала
Изменяем частоту f2 с 2500 Гц на 3627 Гц, получаем график: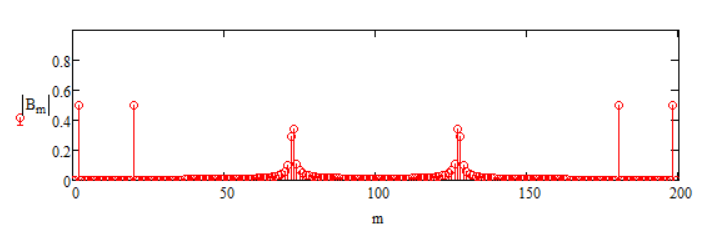



Рис. 11 – Спектр при изменении частоты f2
ДПФ выдает правильный результат только при совпадении гармоник сигнала с аналитическими частотами (бинами), по формуле 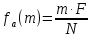, где F – частота дискретизации, а N – количество отсчетов. Если сигнал содержит гармонику, которая не лежит в аналитических частотах, то это отразится на выходных бинах ДПФ – энергия входного сигнала распределится по ним.