Расчет и конструирование станка качалки. 3) СК 960-68 БАК с- 65,97 процентов. Осуществлен расчет основных узлов поверхностного и подземного оборудования
 Скачать 0.76 Mb.
|
|
1.7 Расчет тангенциальных усилий на кольце кривошипа при различных способах уравновешивания Расчет тангенциальных усилий на пальце кривошипа, при различных способах уравновешивания, будем вести по точном теории. Точная теория, в отличие от уточненной и элементарной, учитывает кривизну траектории движения точки В и, следовательно, в наибольшей степени приближают расчеты к действительности. При этом кинематическую схему станка – качалки рассматривают как шарнирный четырехзвенник ОО΄ Д В со сторонами: р, r,ℓ. Определим законы движения звеньев станка – качалки. Определим угол между полюсным расстояниям Р и кривошипом находящимся в крайнем верхнем положении -  о угол о - постоянная величина станка – качалки, он зависит только от размеров звеньев четырехзвенника и характерен для данного станка – качалки:  φо = 35º где Р – полюсное расстояние, Р = 1,8м; ℓ - длина шатуна, ℓ = 1,43м; r – радиус кривошипа , r = 0,57м; в – заднее плечо балансира, в = 1,2м. Все остальные углы поворотов звеньев станка – качалки  , β, γ, и γ2 определяем через каждые 18º поворота кривошипа.Угол между балансира и шатуном β определяем из выражения:   (1)где : φ – угол поворота кривошипа, изменяется от 0º до 360º. Угол γ, расположенный между f и полюсным расстоянием определяем из выражение:  , (2)Угол расположений между f – расстояние между осью балансира и нижней головкой шатуна и полюсным расстоянием Р, определяем из выражения:  , (3)Угол размаха балансира γ равен сумме угла γ1 и γ2 : γ = γ1 + γ2 ; (4) Угол , расположение между кривошипом r и шатуном ℓ находим по формуле: = 360º - (γ + φо + φ + β) ; (5)По формуле (1,2,3,4 и 5) находим значения углов поворотов звеньев станка – качалки через каждый 18º поворота кривошипа и результата вычислений сводим в таблицу 3. Таблица 3 Значение углов поворотов звеньев станка – качалки
продолжение таблицы 3
Определим касательные ускорение точки В для каждого поворота кривошипа по формуле: W =  , (6)где w – угловая скорость кривошипа w=  n – число качений станка – качалки в минуту, n = 12 кач./мин; β – угол между шатуном и балансира берем из табл. 1; - угол между кривошипом и шатуном берем из табл. 1;r - отношение радиуса кривошипа к заднему плечу кривошипа; r - отношение радиуса кривошипа к длине шатуна. По формуле (6) определяем касательные ускорение точки В через каждые 18º поворота кривошипа и результаты вычислений сводим в таблицу 4. Таблица 4
Теперь можем, определит тангенциальные усилия на пальце кривошипа, при каждом повороте его на 18º. При балансирном уравновешивании станков – качалок, применяются устройство, состоящее из грузов в виде плит , которые закрепляют на хвосте балансира. Тангенциальные усилия при балансирном уравновешивании находится по следующей формуле: а) ход точки подвеса штанг вверх:  , (7) б) ход точки подвеса штанг вниз:   (8)где Рш – вес колонны насосных штанг; Рш = qш · L · g = 2,35 · 960 · 9,81 = 22131 Н; qш– масса 1м штанг 19мм с муфтами, qш = 2,35кг; L – глубина подвески насоса, L = 960м; g – ускорения свободного падения, g = 9,81 мс; Gж – вес жидкости, поднимаемой на дневную поверхность. Gж = [ (Fпл – fш) L · γж · g – Fпл · γж · · g ] =(6,15 – 2,83) · 960 · 850 · 9,81 – - 6,15 · 850 ·20 · 9,81 = 2555 Н. Fпл– площадь сечение плунжера диаметром 28мм, Fпл = 6,15см²; fш – площадь сечение штанг диаметром 19мм, fш = 2,83см²; γж – удельный вес жидкости, поднимаемой на дневную поверхность. γж = 850 кг/м³. - глубина погружения насоса под динамический уровеньВес балансирных грузов Xо находим по формуле:   - отношение длины переднего плеча балансира к заднему   - отношение расстояние от оси балансира до центра тяжести груза к заднему плечу балансира  Находим постоянные величины: а) для хода точки подвеса штанг вверх (Рм + Gж) в = (22131 + 2555) · 1 = 24686 Н 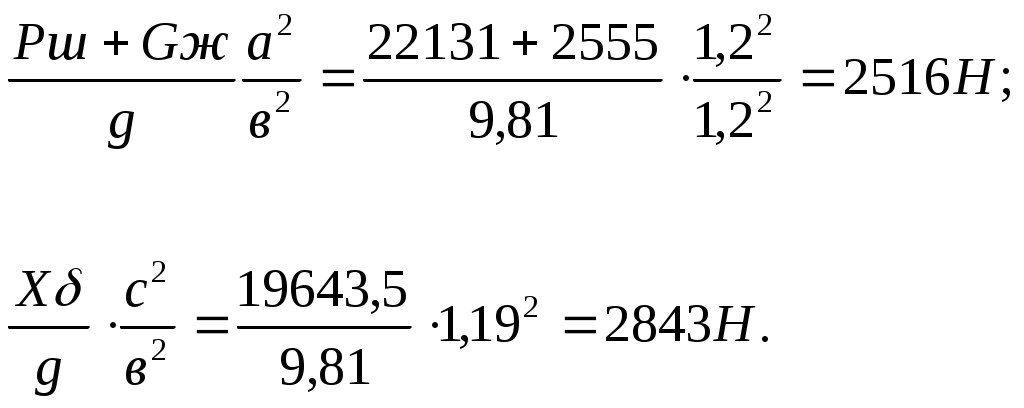  б) для хода точки подвеса штанг вниз Рш = 22131 Н: Углы , β, φо и γ берем из таблицы 3. Касательное ускорение точкиβ - Wв берем из таблицы 4. При роторном уравновешивание противовес помещают на кривошипе, с которым он вращается, составляя одно целое – ротор. Так как противовес вращается с постоянной угловой скоростью, то не возникают инерциальные силы. Тангенциальные усилия при роторном уравновешивании определяются из следующих формул: а) ход точки подвеса штанг вверх:  , (9)б) ход точки подвеса штанг вниз Gж = 0  , (10) Вес роторных грузов определяем по формуле: XR = qR · nR = 5700 · 4 = 22800 Н; где qR – вес одного противовеса на кривошипе qR = 5700 Н nR – число противовесов на кривошипах nR = 4 Регулируют уравновешивание перемещением грузов вдоль кривошипа. Исходя из этого, определяем радиус расположения центра тяжести роторных грузов: R=  Определим постоянные величины: а) для хода точки подвеса штанг вверх. (Рш + Gж) в = 246,86 Н; XR·  ;  б) для хода точки подвеса штанг вниз. Gж = 0: Рш = 22131 НУглы , β и φ берем из таблицы 3. Касательное ускорение точки В – Wв находим в таблице 4.Комбинированное уравновешивание это комбинация балансирного и роторного уравновешивания. Применяются они в станках – качалках для средних нагрузок, когда применение балансирного уравновешивания приводит к большим силам инерции от противовеса. Тангенциальные усилия при комбинированном способе уравновешивания определяются по следующим формулам: а) ход точки подвеса штанг вверх.  , (11)б) ход точки подвеса штанг вниз. Тк = Ршв sinβ - Xбв sinβ sin (φо + γ) - XR r sin φ + gв² , (12) При комбинированном уравновешивании на хвосте балансира закреплено определенное количество плит общим весом Xб, а на кривошипах – роторные грузы, общим весом XR. Уравновешивание регулируют перемещением роторных грузов. Задаемся весом грузов на балансире: XR = Rв (Рш + 2 ) · Rв Xб = 0,585 XR =  Находим постоянные величины. а) для хода точки подвеса штанг вверх. ( Рш + Gж) в = 24686 Н; Xбв = 9000 · 1,2 = 10725 Н; б) для хода точки подвеса штанг вниз Ршв = 22131 Н; Углы , β, φ, φо и γ находим в таблице 3. Касательные ускорение точки В – Wв берем из таблицы 4.По формулам (7, 8, 9, 10, 11, 12,) определяем тангенциальные усилия на кольце кривошипа, при каждом повороте его на 18° и результаты вычисление сводим в таблицу 5. Таблица 5
продолжение таблицы 5
По результатам вычислений строим диаграммы тангенциальных усилий для различных способов уравновешивания станка – качалки. Для этого по оси абсцисс отложим значения угла φ, а по оси ординат – значения тангенциальных усилий при роторном ТR, балансирном Тб и комбинированном Тк уравновешиваниях. |