Холл. Отчет. Изучение эффекта Холла в полупроводниках Работу выполнили Студенты гр. Ф172 Волков Д. М., Лужных А. С
 Скачать 214.52 Kb. Скачать 214.52 Kb.
|
1 2 ВыводВ ходе эксперимента мы изучили эффект Холла и рассчитали постоянную Холла R, концентрацию n и подвижность 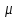 для данного полупроводника. для данного полупроводника.Ответы на контрольные вопросы1. Приведите примеры кинетических явлений в твердых телах. Кинетические явления лежат в основе фотоэлектронных и фотомагнитных эффектов. Стакан, песок – да любое твердое тело сохраняет свою форму неизменной. 2. Кинетическое уравнение Больцмана для функции распределения. Условия применимости. Уравнение Больцмана является интегро-дифференциальным. Его решения в общем виде не получено. Для стационарного случая, когда (f/t) = 0, кинетическое уравнение имеет вид: 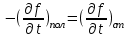 . Что означает, что в стационарном состоянии изменения функции распределения, создаваемое внешними полями и движением частиц компенсируется столкновениями носителей заряда с локальными нарушениями периодичности поля решетки. Если (f/t)пол(f/t)ст , то (f/t) 0 и функция распределения меняется во времени в ту или иную сторону, в зависимости от превалирования определенного процесса. . Что означает, что в стационарном состоянии изменения функции распределения, создаваемое внешними полями и движением частиц компенсируется столкновениями носителей заряда с локальными нарушениями периодичности поля решетки. Если (f/t)пол(f/t)ст , то (f/t) 0 и функция распределения меняется во времени в ту или иную сторону, в зависимости от превалирования определенного процесса.Решение кинетического уравнения значительно упрощается вводом так называемого времени релаксации. Предположим, что в некоторый момент времени t = 0 полевой член обращается в нуль (Выключается поле). 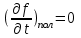 или или 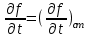 3. Смысл полевого члена и интеграла столкновений стационарного кинетического уравнения Больцмана. Выражение (f/t)пол носит название полевого члена уравнения Больцмана, отражает действие внешних сил. Обозначим через (f/t)ст –интеграл столкновений, изменение функции распределения в результате соударений. общее изменение функции распределения во времени представим в виде суммы полевого члена и интеграла столкновения. 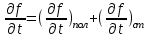 4. Определите плотность электрического тока и потока энергии. Плотность электрического тока — векторная физическая величина, имеющая смысл силы электрического тока, протекающего через элемент поверхности единичной площади. Поток энергии — это количество энергии, переносимое через некоторую произвольную площадку в единицу времени. 5. Определите подвижность и дрейфовая скорость носителей заряда. 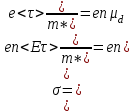 , ,где n – концентрация носителей заряда, m* тензор эффективной массы, t время релаксации, а 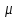 d – тензор подвижности носителей заряда. Удельная проводимость d – тензор подвижности носителей заряда. Удельная проводимость 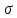 и подвижность и подвижность 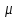 d определяются усредненным временем релаксации < d определяются усредненным временем релаксации < 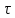 > с весом Е. > с весом Е.В скрещенных полях Е и B движение без начальной скорости идет по циклоиде радиуса R и с дрейфовой скоростью Ud в направлении перпендикулярно электрическим и магнитным полям. 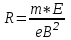 , ,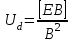 . .6. Закон Ома. Электропроводность полупроводников. Сила тока на участке цепи прямо пропорциональна напряжению на этом участке и обратно пропорционально его сопротивлению. закона Ома Из значения коэффициента Холла для одно и того же образца можно определить концентрацию носителей заряда из выражения (), а, зная электропроводность 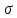 =en =en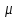 , можно вычислить холловскую подвижность, как , можно вычислить холловскую подвижность, как 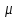 =|R|. =|R|.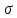 . И это в случаи несмешанного полупроводника . И это в случаи несмешанного полупроводника7. Состав выражения для плотности тока в полупроводнике во внешнем поле. При приложении внешнего электрического поля в полупроводнике появится направленная, «дрейфовая» компонента скорости E – по полю у дырок, против поля – у электронов, т.е. через образец потечет электрический ток. Плотность тока j будет складываться из плотностей «электронного» jn и «дырочного» jp токов: j jn jp enn epp , (2) где n, p - концентрации свободных электронов и дырок; υn , υp – дрейфовые скорости носителей заряда. 8. Оценка слабых и сильных магнитных полей для гальваномагнитных эффектов. Наряду с поперечными Г. я. наблюдается также небольшое изменение сопротивления металлов в магнитном поле, параллельном току I: ( 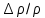 )||, наз. продольным гальваномагнитным эффектом. В сильных магнитных полях обнаруживаются квантовые эффекты, проявляющиеся в немонотонной (осциллирующей) зависимости постоянной Холла и сопротивления от поля Н. )||, наз. продольным гальваномагнитным эффектом. В сильных магнитных полях обнаруживаются квантовые эффекты, проявляющиеся в немонотонной (осциллирующей) зависимости постоянной Холла и сопротивления от поля Н.В слабых магнитных полях ( 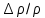 ) )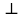 пропорционально H2. Коэффициент пропорциональности между ( пропорционально H2. Коэффициент пропорциональности между (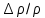 ) )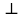 и H2 положителен, т. е. сопротивление растет с увеличением магнитного поля. Изменение сопротивления в магнитном поле называется чётным гальваномагнитных явлений, т. к. ( и H2 положителен, т. е. сопротивление растет с увеличением магнитного поля. Изменение сопротивления в магнитном поле называется чётным гальваномагнитных явлений, т. к. (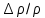 ) )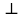 не изменяет знак при изменении направления поля Н на обратное. не изменяет знак при изменении направления поля Н на обратное.9. Движение частиц в электромагнитных полях. Движения частицы в электрическом и магнитном поле под действием силы Лоренца: 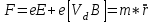 , , где m* эффективная масса носителей заряда. В одном магнитном поле движение происходит по кругу со скоростью V поперек поля B, по радиусу R, с угловой скоростью w. 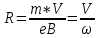 , , 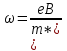 . .Электрическое поле увеличивает только продольную составляющую скорости. В скрещенных полях Е и B движение без начальной скорости идет по циклоиде радиуса R и с дрейфовой скоростью Ud в направлении перпендикулярно электрическим и магнитным полям. 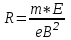 , , 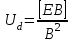 . .10. Классификация гальвано-магнитных эффектов. Гальваномагнитными эффектами называются физические эффекты, возникающие в веществе, находящемся в магнитном поле, при прохождении через вещество электрического тока под действием электрического поля. Гальваномагнитные эффекты возникают под действием поперечного магнитного поля при протекании через образец электрического тока. В то же время для термомагнитных эффектов, сопутствующих гальваномагнитным, первичными являются тепловой поток и нормальное к нему магнитное поле. Классификация гальвано– и термомагнитных эффектов  11. Элементарная теория эффекта Холла. Если полупроводник, по которому протекает электрический ток, поместить в магнитное поле, то в нем возникает ряд эффектов. Физические явления, возникающие в веществе, находящемся в магнитном поле, при прохождении через него электрического тока, называются гальваномагнитными явлениями (эффектами). К гальваномагнитным явлениям относят эффект Холла и магнетосопротивление. 12. Как определить знак и подсчитать концентрацию носителей заряда в опыте по эффекту Холлу? Так как ЭДС Холла меняет знак на обратный при изменении направления магнитного поля на противоположное направление, то эффект Холла относится к нечётным гальваномагнитным явлениям. Эту немагнитную составляющую разности потенциалов необходимо исключить, замерив напряжение при двух противоположенных полярностях магнитного поля U+ и U-. Далее, в случае, когда Uн>U0, а знаки U+ и U- разные и совпадают со знаками Uн: U+ = U0 + Uн, -U- = U0 – Uн, Uн = (|U+| + |U-|)/2. Или, когда Uн U+ = U0 + Uн, U- = U0 – Uн, Uн = (|U+| - |U-|)/2. 13. Как определить постоянную Холла?  Для определения типа основной примеси в полупроводнике (донорная или акцепторная) кроме абсолютного знака R существенно, что в п/п p-типа с ростом температуры и при переходе из области примесной проводимости в область собственной проводимости постоянная Холла R меняет знак. Поэтому из кривой R(T) в соответствующем интервале температур можно определить тип примесной проводимости. 1 2 |
