Лабораторная работа 1 ЭСиЭ. Отчет к лабораторным работам по дисциплине Математическое моделирование электрических систем и элементов

• Название: Отчет к лабораторным работам по дисциплине Математическое моделирование электрических систем и элементов
• Дата: 14.02.2022
• Размер: 375.59 Kb.
• Имя файла: Лабораторная работа 1 ЭСиЭ.docx
• Тип: Отчет; #361745
• страница: 3 из 3

Лабораторная работа №5

Прогнозирование годовой выработки электроэнергии на основе экспоненциальной и логистической моделей в среде MathCaD

1). Выполнить прогноз годовой выработки электроэнергии по данным, приведенным в табл. 1, на 2000 и 2005 годы.

Таблица 1

Годовая выработка электроэнергии в СССР, млрд. кВт·ч

Годы (ti)	1960	1965	1970	1975	1980	1985	1990
Wi	292	506	740	1038	1293	1544	1726

Для прогнозирования выберем экспоненциальную и логистическую модель

Для определения  в 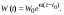найдем логарифмы W_i и найдем коэффициенты линейной функции .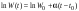

Таблица 2

Логарифмы W_i

(ti – t0)	0	5	10	15	20	25	30
Ln Wi	5,677	6,227	6,607	6,945	7,165	7,342	7,454

Здесь i = 0, 1, 2, …, n – 1 (n = 7).

Все расчеты и графические построения выполнить в Mathcad.

Начальные значения:

Обозначения: Years – годы, W – годовое электропотребление, t_n – первый год ретроспективы.







1. Экспоненциальная модель



В логарифмических координатах – линейная зависимость:



Экспоненциальная функция:





2. Логистическая модель 1

Для получения параметров логистической модели требуется дифференцирование функции ln W(t). Для функции, заданной дискретными значениями, получим n – 1 точек ее производной



Прологарифмируем значения _j и запишем их в табл. 3.



(значений  на единицу меньше, чем значений W)

Таблица 3

Значения  и логарифмы 

(ti – t0)	0	5	10	15	20	25
	0,11	0,076	0,068	0,044	0,035	0,022
ln	–2,208	–2,577	–2,693	–3,125	–3,339	–3,804

Построим график логарифма производной от энергии W (квадратиками обозначены дискретные значения из табл. 3). На графике показано, как ломаная кривая дискретных значений аппроксимируется прямой линией.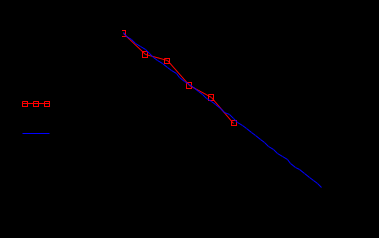





Запишем функции для логистической модели:



С учетом знака минус :





Построим графики логарифмов экспоненциальной и логистической модели: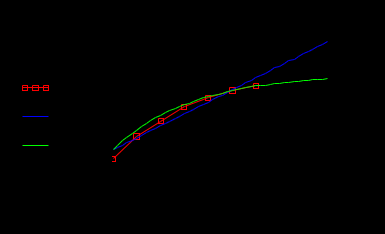



На графике видно, что логистическая зависимость дает более точные совпадения с экспериментальными данными.

Построим графики самих математических моделей: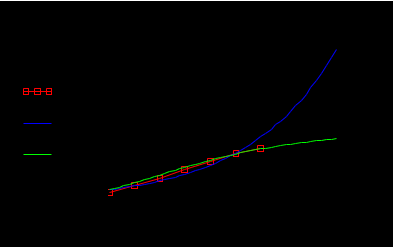



В системе Mathcad имеются специальные функции проведения регрессии для некоторых наиболее распространенных моделей, в том числе для экспоненциальной и логистической модели:

expfit(vx, vy, vg) – возвращает вектор, содержащий коэффициенты (a, b и c) аппроксимирующего выражения экспоненциальной модели вида , график которого лучшим образом приближается к точкам, координаты которых хранятся в векторах vx и vy (вектор vg содержит первое приближение к решению);

lgsfit(vx, vy, vg) – возвращает вектор, содержащий коэффициенты (a, b и c) аппроксимирующего выражения логистической модели вида 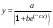, график которого лучшим образом приближается к точкам, координаты которых хранятся в векторах vx и vy (вектор vg содержит первое приближение к решению).

Выполним моделирование по указанным функциям.

Экспоненциальная модель 2





Логистическая модель 2





Графические построения по обеим моделям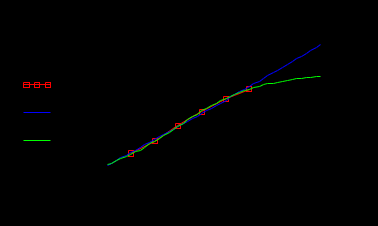





В системе Mathcad есть функция линейного алгебраического предсказывания predict. Она применяется для гладких и периодических функций и является разновидностью экстраполяции.

predict(v, m, n) – возвращает n предсказанных значений, основанных на m последовательных значениях вектора данных v. v – представляет собой вектор равномерно расположенных данных (через равные интервалы по аргументу).

Функция predict использует последние m исходных значений данных, чтобы вычислить коэффициенты предсказания. Как только это сделано, она использует последние m точек, чтобы предсказать координаты m + 1-й точки, фактически создавая скользящее окно шириной в m точек.

Выполним прогноз выработки электроэнергии с помощью этой функции:



Графическая сравнительная иллюстрация моделей из инструментальных средств Mathcad.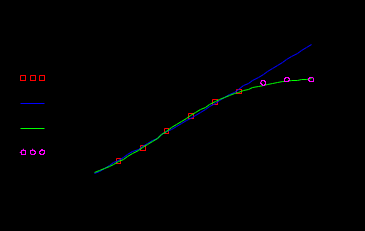



Оценка погрешностей моделей и численные значения прогноза на 2000 и 2005 годы.









Заключение:

В ходе выполнения лабораторных работ были получены следующие умения:

- формулировать сущность проблемы, цели и задачи, принимать основные допущения;

– проводить эксперименты по заданным методикам с последующей обработкой и анализом результатов в области электроэнергетики;

– составлять математическую модель процесса, применяя законы электротехники;

– составлять схемы замещения элементов энергосистемы и рассчитывать их параметры.

Навыки:

работы в программном комплексе MathCad при математическом моделировании различных режимов работы элементов электрических систем, расчета токов и напряжений для простейших схем в установившемся и переходном режимах.