Лабораторная работа 1 ЭСиЭ. Отчет к лабораторным работам по дисциплине Математическое моделирование электрических систем и элементов
 Скачать 375.59 Kb. Скачать 375.59 Kb.
|
|
ФГБОУ ВО Уфимский государственный авиационный технический университет Кафедра электромеханики Отчет к лабораторным работам по дисциплине «Математическое моделирование электрических систем и элементов» Выполнил: Группа Фамилия И.О., Фамилия И.О., Фамилия И.О., Проверил: к.т.н., доцент Гусаков Д. В. Уфа 2018 Цель работы: Научится формулировать сущность проблемы, цели и задачи, принимать основные допущения; – проводить эксперименты по заданным методикам с последующей обработкой и анализом результатов в области электроэнергетики; – составлять математическую модель процесса, применяя законы электротехники; – составлять схемы замещения элементов энергосистемы и рассчитывать их параметры. Овладеть - навыком работы в программном комплексе MathCad при математическом моделировании различных режимов работы элементов электрических систем, расчета токов и напряжений для простейших схем в установившемся и переходном режимах. Лабораторная работа №1 Исследование режимов холостого хода и передачи мощности по ЛЭП 1). Найти распределение величины напряжения и тока вдоль ЛЭП 500 кВ длиной L = 500 км при холостом ходе и при передаче мощности нагрузки меньше и больше натуральной мощности линии. Конструкция фазы линии: 3хАС-400/51. Расчеты и графические построения выполнить в системе Mathcad. Приведенные ниже значения параметров линии выражены в омах, сименсах и радианах. Параметры режима ЛЭП даны в киловольтах, килоамперах, мегаваттах и мегаварах. Длина и погонные параметры линии:  Расчетные параметры линии – волновое сопротивление, коэффициент распространения волны и натуральная мощность:  1. Режим холостого хода Напряжение в конце линии: Построение графика напряжения вдоль линии в режиме холостого хода: 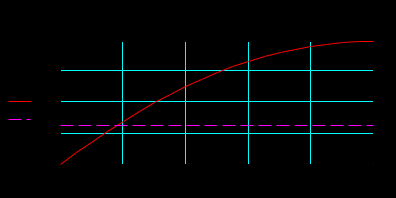 Построение графика тока вдоль линии в режиме холостого хода: 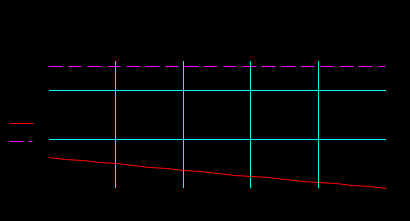 Из полученных зависимостей видно, что напряжение вдоль ЛЭП начинает превышать предельно допустимое значение уже на расстоянии около 100 км от начала линии; такой режим в действительности неосуществим из-за перекрытия изоляции на линии. Ток по линии имеет наибольшее значение в начале линии и не превышает допустимое значение, равное 2,475 кА. 2. Режим передачи мощности меньше натуральной Натуральная мощность данной ЛЭП равна 859,9 МВт. Возьмем передаваемую мощность 700 МВт, реактивную мощность в конце линии примем равной нулю: Напряжение в конце ЛЭП найдем из решения системы уравнений. Начальные приближения для неизвестных U2, I2:  Решающий блок:  Результаты решения системы уравнений (напряжение и ток в конце линии):  Вектор напряжения в конце линии отстает от вектора напряжения в начале на 24,473 градуса. 3. Режим передачи мощности больше натуральной Примем передаваемую активную мощность по линии 900 МВт. Можно убедиться, что при реактивной мощности в конце линии, равной нулю, режим напряжений по линии является неудовлетворительным. Для поддержания удовлетворительного напряжения требуется реактивная мощность емкостного характера. Пусть мощность компенсирующего устройства, включенного в конец линии, такова, что в конце линии реактивная мощность равна минус 100 Мвар (передается в линию). Напряжение в конце ЛЭП найдем из решения системы уравнений. Начальные приближения для неизвестных U2, I2: Решающий блок:  Результаты решения системы уравнений (напряжение и ток в конце линии):  Построим графики напряжения и тока вдоль линии для обоих режимов передачи мощности. Функция напряжения для P2 < Pнат : Функция напряжения для P2 > Pнат : 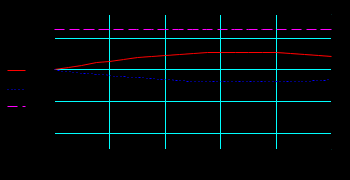 Функция тока для P2 < Pнат : Функция тока для P2 > Pнат : 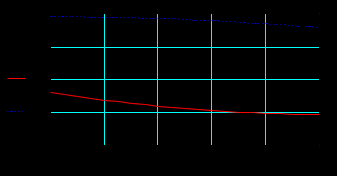 Изменение активной и реактивной мощности вдоль ЛЭП для двух режимов:  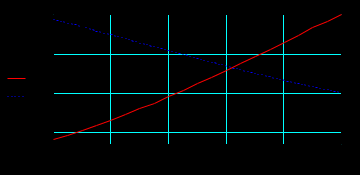 Значения активной мощности к началу линии возрастают в обоих случаях, так как вдоль линии имеют место потери активной мощности. Реактивная мощность в первом случае, когда реактивной нагрузки в конце линии нет, передается к началу линии (отрицательные значения) из-за преобладания зарядной мощности над потерями реактивной мощности. Во втором случае имеет место обратная картина: потери реактивной мощности больше зарядной и потери компенсируются источником реактивной мощности в конце линии. 2). Выполнить оценку погрешностей двух упрощенных математических моделей ЛЭП – уравнений идеальной линии и уравнений для П-образной схемы замещения без учета распределенности параметров – для конкретной ЛЭП 500 кВ. Для этого построить зависимости напряжения в начале линии U1 от длины линии при передаче мощности нагрузки, близкой к натуральной мощности линии. Конструкция фазы линии: 3хАС-400/51. Расчеты и графические построения выполнить в системе Mathcad. Приведенные ниже значения параметров линии выражены в омах, сименсах и радианах. Параметры режима ЛЭП даны в киловольтах, килоамперах, мегаваттах и мегаварах. Длина и погонные параметры линии:  Передаваемая мощность и напряжение в конце линии: Расчетные параметры ЛЭП:  Для идеальной линии:  Определим функции напряжения и тока в начале линии для трех моделей ЛЭП:  Относительные погрешности напряжения в начале линии: Графики напряжений в начале линии: 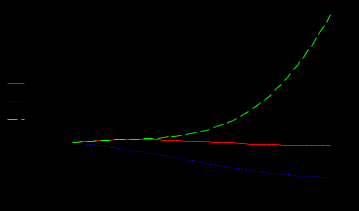 Графики относительных погрешностей напряжения в начале линии для упрощенных математических моделей: 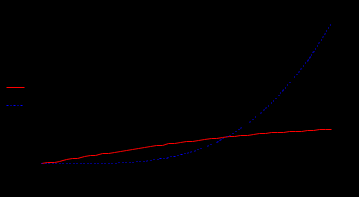 Примем допустимую относительную погрешность в вычислении напряжения – 1 %. Из графиков погрешностей видно, что погрешность в определении напряжения в начале линии для модели идеальной линии превышает допустимую уже при 120 км, а по току – при 600 км; погрешность для модели без учета распределенности параметров допустима для линий длиной до 500 км. Аналогичные графики погрешностей можно построить для указанных моделей для тока в начале линии. Лабораторная работа №2 Построение внешней характеристики трансформатора 1). Определить функцию как решение системы уравнений. Для удобства записи введем еще две переменные I'2 = I2 cos φ и I''2 = I2 sin φ. Начальные приближения: Решающий блок Mathcad:  Функция как решение системы уравнений: Здесь функция F является вектор-функцией, т. е. содержит пять элементов (по числу неизвестных). Первый элемент дает функцию U2, второй – U′1 и т. д. Нас интересует только первый элемент: функция U2 от I2 и cos φ. Если переменная ORIGIN в Mathcad имеет заданное по умолчанию значение 0, то наша функция будет использоваться в виде F(I2, cosφ)0. Так, например, для cos φ = 0,8 выходная характеристика будет строиться по функции F(I2, 0.8)0 при изменении тока от 0 до Iном. 2). Построить внешнюю характеристику силового трансформатора ТРДЦН-63000/110 по его математической модели – Г-образной схеме замещения. Расчеты и построение характеристики выполнить в Mathcad. Напряжения в киловольтах, мощности в киловольт-амперах, токи в килоамперах, сопротивления в омах, проводимости в сименсах. Параметры трансформатора: Номинальный ток, коэффициент трансформации и параметры ветви намагничивания:  Коэффициенты А и В четырехполюсника: Условия построения характеристики: Начальные приближения: Решающий блок Mathcad:  Внешние характеристики для трех значений коэффициента мощности: 1; 0,9 и 0,8:  Снижение напряжения на вторичной обмотке с ростом тока нагрузки вызвано потерей напряжения в сопротивлениях обмоток трансформатора. Для того чтобы не допустить снижения напряжения у потребителей электроэнергии, в силовых трансформаторах предусмотрено специальное устройство – регулятор напряжения, который при росте тока нагрузки изменяет коэффициент трансформации таким образом, чтобы обеспечить необходимое напряжение на шинах вторичного напряжения трансформатора. Получим внешнюю характеристику трансформатора по его упрощенной модели, в которой не учитываются активные параметры: Rт = 0 и Gµ = 0, и сопоставим полученные характеристики с характеристиками, полученными по полной модели. Коэффициенты А и В четырехполюсника для упрощенной модели: Начальные приближения: Решающий блок Mathcad:  Внешние характеристики для трех значений коэффициента мощности: 1; 0,9 и 0,8:  Вычислим и построим функции погрешностей внешних характеристик упрощенной модели:  Из последнего рисунка видно, что погрешности характеристик упрощенной модели не превышают 0,4 %. Такая погрешность вполне допустима во многих задачах расчета установившихся режимов и токов короткого замыкания в электрических системах и поэтому иногда активным сопротивлением обмоток трансформатора и потерями в стали пренебрегают. Следует, однако, заметить, что для трансформаторов малой мощности такая картина не сохраняется и применение упрощенной модели становится более ограниченным. Лабораторная работа №3 Расчет установившегося режима ЭЭС на основе линейных и нелинейных математических моделей 1). Рассчитать напряжения в узлах и токи в ветвях схемы электрической сети, граф которой изображен на рис. 1. Исходные данные для расчета и расчет представлены в системе Mathcad. 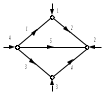 Рис. 1. Пример графа электрической сети  Исходные данные Напряжение базисного узла 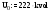 Сопротивления ветвей и задающие токи узлов:  Расчетные данные  Модель электрической сети 1. Составление матрицы инциденций узлов и ветвей M:  2. Формирование диагональной матрицы проводимостей ветвей Y:  3. Составление матрицы-столбца проводимостей ветвей, связывающих узлы схемы с базисным узлом Y0:  4. Получение матрицы узловых проводимостей Y:  Вычисления 1. Решение системы линейных уравнений методом обратной матрицы:   2. Расчет других параметров режим сети:  Напряжение ветвей   3. Проверка результатов: сумма задающих токов должна быть равна току балансирующего узла с обратным знаком:  Сумма задающих токов   |
