Расчет надёжности системы с учетом технического обслуживания и восстановления повреждений. Отчет к лабораторной работе 2 Расчет надёжности системы с учетом технического обслуживания и восстановления повреждений по дисциплине Надежность акс
 Скачать 70.49 Kb. Скачать 70.49 Kb.
|
|
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ Федеральное государственное бюджетное образовательное учреждение высшего образования «МОСКОВСКИЙ АВИАЦИОННЫЙ ИНСТИТУТ (национальный исследовательский университет)» (МАИ) Кафедра 604 “Системный анализ и управление” Специальность 24.03.03 “Баллистика и гидроаэродинамика” Отчет к лабораторной работе №2 «Расчет надёжности системы с учетом технического обслуживания и восстановления повреждений» по дисциплине «Надежность АКС». Вариант 2. Работу выполнили студенты группы М6О-401Б-19 А.Р. / / Белозерцева А.Н. / / Бюн Ю. / / Пятницкий П.В. / / Работу принял преподаватель кафедры 604 Пельтихин А.В. / / Москва 2023 Оглавление Постановка задачи 3 Порядок выполнения работы 4 Результаты 5 Выводы 7 Приложение 8 Постановка задачиСчитается, что в некоторой авиационной системе перед отказом имеет место накопление повреждений, которые можно обнаружить в процессе периодических технических проверок и устранения возникших повреждений до того, как они приведут к отказу системы. Структурная схема надёжности системы: 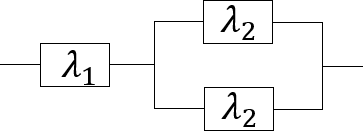 Здесь 𝜆1, 𝜆2 - интенсивности отказа элементов. Предполагается, что времена безотказной работы элементов распределены по экспоненциальному закону. Вероятность безотказной работы системы за один час полёта должна быть не хуже Ρ = 0,99995. Целью работы является расчет надёжности системы с учетом технического обслуживания и восстановления повреждений. Исходныеданные
Порядок выполнения работыОпределить максимально возможное время между проверками системы, если интенсивность отказов нерезервированной части λ1= 2,5 * 10−4 ч-1, а интенсивность отказов канала в резервированной части λ2= 5 * 10−4 ч-1. Построить зависимость периодичности проверок от значения вероятности безотказной работы. Определить область возможных значений интенсивностей λ1 и λ2, обеспечивающих требуемое значение вероятности безотказной работ, если периодичность проверок не может быть больше ∆𝑡 часов. Определить оценку математического ожидания и дисперсии времени безотказной работы системы при отсутствии периодических проверок. РезультатыМаксимально возможное время между проверками системы: 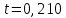 Зависимость периодичности проверок от значения вероятности безотказной работы: 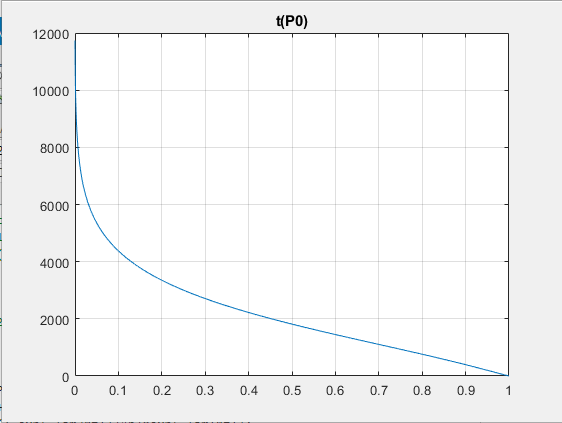 Область возможных значений интенсивности: 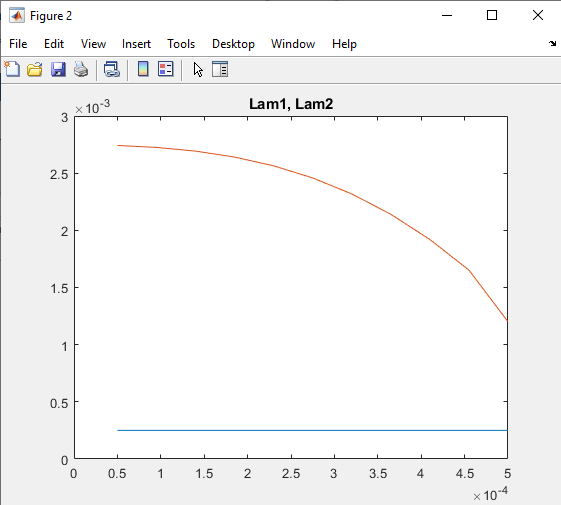 Оценки статистических характеристик времени безотказной работы системы при отсутствии периодических проверок: Оценки статистических характеристик времени безотказной работы системы при отсутствии периодических проверок: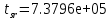 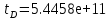 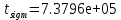 ВыводыВ ходе работы был проведен расчет надежности системы с учетом технического обслуживания (периодических проверок) и восстановления повреждений. Было определено: максимально возможное время между проверками системы, если интенсивность отказов нерезервированной части λ1= 2,5 * 10−4 ч-1, а интенсивность отказов канала в резервированной части λ2= 5 * 10−4 ч-1, обеспечивающее вероятность безотказной работы не меньше заданной. Показано, что требуемое время между проверками системы увеличивается с уменьшением вероятности безотказной работы. Построена область возможных значений интенсивностей, обеспечивающих требуемое значение вероятности безотказной работы. Путём многократной имитации работы системы оценены математическое ожидание и дисперсия времени безотказной работы системы при отсутствии периодических проверок. Приложениеclc, clear lam1 = 2.5e-4; lam2 = 5e-4; t1=0; n = 3; dt = 50; Pk(1) = 0.99995; % от 0.7 dp=0.00035; p=1; t(1)=0.2; lm10=10^-6; lm20=10^-6; lm1=lm10; lm2=lm20; % % %%%%%%%%%11111111111%%%%%%%%%%%% % while p>=Pk(1) % t1=t1+0.01 % p=(1-(1-exp(-lam1*t1))^n)*exp(-lam2*t1); % vpa(p,6) % end N=857; %%%%%%%%%%2222222222222%%%%%%%%%%%% % for i=1:N % t1=0; % p=1; % while p>=Pk(i) % t1=t1+0.1; % p=(1-(1-exp(-lam1*t1))^n)*exp(-lam2*t1); % %vpa(p,5); % end % Pk(i+1)=Pk(i)-dp; % t(i+1)=t1; % i=i+1; % end % % figure(1) % plot(Pk, t), grid on % title ('t(P0)') % % %%%%%%%%%333333333333%%%%%%%%%%%% % Pkonech=0.99995; % lamda2(1)=5e-4; % dlamda2 = 0.000045; % lammin(1)=lam1; % lammax(1)=0.0012 ; % lammin1=0; % for i=1:10 % t2=0; % j=0; % lamda1j(1)=lam1; % while t2<=50 % % j=j+1; % t2=t2+5; % lamda1=-log(Pkonech/(1-(1-exp(-lamda2(i)*t2)).^n))*t2; % lamda1j(j)=lamda1 % vpa(lamda1j,7); % end % lammin(i+1)=lamda1j(1); % lammax(i+1)=lamda1j(11) % vpa(lammin,7); % vpa(lammax,7); % lamda2(i+1)=lamda2(i)-dlamda2; % i=i+1; % t(i+1)=t2 % end % figure(2) % plot(lamda2, lammin,lamda2,lammax) % title ('Lam1, Lam2') 444444444444 i=1; T_=[]; for i=1:1000 tsv1=exprnd(1/lm1); tsv2_1=exprnd(1/lm2); tsv2_2=exprnd(1/lm2); tsv2_3=exprnd(1/lm2); tmax=max(tsv2_1,tsv2_2) tsv=min(tsv1,max(tmax,tsv2_3)); T_(i)=tsv; end t_sr=mean(T_) lm=1/t_sr; t_D=1/(lm^2) t_sigm=sqrt(t_D) |
