Отчет по практике. Отчет. Отчет Лабораторная работа 1 "Маятник" студент группы ет310 Корнилова О. Е
 Скачать 68.33 Kb. Скачать 68.33 Kb.
|
|
Министерство науки и высшего образования Российской Федерации Федеральное государственное автономное образовательное учреждение высшего образования «Южно-уральский государственный университет (национальный исследовательский университет)» Институт естественных и точных наук Отчет Лабораторная работа №1 "Маятник" Выполнил: студент группы ЕТ-310 Корнилова О.Е Проверил: преподаватель кафедры ВМ Стариков Я.Е. Челябинск – 2021 Постановка задачи 1. Произвести расчет траектории маятников с незатухающими и затухающими колебаниями, используя язык программирования С++. Отрезок времени 100 сек, шаг расчета 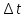 = 1 сек, коэффициент затухания = 1 сек, коэффициент затухания 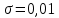 . Начальная амплитуда при . Начальная амплитуда при 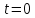 , , 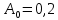 м. м. 2. Результаты расчетов записать в файл. 3. Построить графики координат маятников от времени, используя функции Matlab. 4. Сделать выводы и составить отчет. Теоретическая часть Затухающие колебания – колебания, амплитуды которых из-за потерь энергии реальной колебательной системой с течением времени уменьшаются. Простейшим механизмом уменьшения энергии колебаний является ее превращение в теплоту вследствие трения в механических колебательных системах, а также омических потерь и излучения электромагнитной энергии в электрических колебательных системах. Закон затухания колебаний определяется свойствами колебательных систем. Обычно рассматривают линейные системы – идеализированные реальные системы, в которых параметры, определяющие физические свойства системы, в ходе процесса не изменяются. Линейными системами являются, например, пружинный маятник при малых растяжениях пружины (когда справедлив закон Гука), колебательный контур, индуктивность, емкость и сопротивление которого не зависят ни от тока в контуре, ни от напряжения. Различные по своей природе линейные системы описываются идентичными линейными дифференциальными уравнениями, что позволяет подходить к изучению колебаний различной физической природы с единой точки зрения, а также проводить их моделирование, в том числе и на ЭВМ. Дифференциальное уравнение свободных затухающих колебаний линейной системы задается в виде 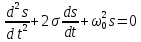 где 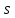 – колеблющаяся величина, описывающая тот или иной физический процесс, – колеблющаяся величина, описывающая тот или иной физический процесс, 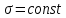 – коэффициент затухания, – коэффициент затухания, 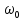 – циклическая частота свободных незатухающих колебаний той же колебательной системы, т. е. при – циклическая частота свободных незатухающих колебаний той же колебательной системы, т. е. при 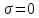 (при отсутствии потерь энергии) называется собственной частотой колебательной системы. (при отсутствии потерь энергии) называется собственной частотой колебательной системы. Решение уравнения рассмотрим в виде 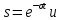 где 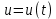 . После нахождения первой и второй производных выражения и подстановки их получим . После нахождения первой и второй производных выражения и подстановки их получим 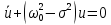 Решение уравнения зависит от знака коэффициента перед искомой величиной. Рассмотрим случай, когда этот коэффициент положителен: 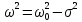 (если 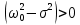 , то такое обозначение мы вправе сделать). Тогда получим уравнение, решением которого является функция , то такое обозначение мы вправе сделать). Тогда получим уравнение, решением которого является функция 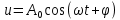 . Таким образом, решение уравнения в случае малых затуханий . Таким образом, решение уравнения в случае малых затуханий 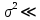 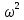 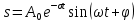 где 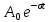 – амплитуда затухающих колебаний, а – амплитуда затухающих колебаний, а 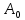 – начальная амплитуда Промежуток времени, в течение которого амплитуда затухающих колебаний уменьшается в – начальная амплитуда Промежуток времени, в течение которого амплитуда затухающих колебаний уменьшается в 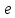 раз, называется временем релаксации. раз, называется временем релаксации. Затухание нарушает периодичность колебаний, поэтому затухающие колебания не являются периодическими и, строго говоря, к ним неприменимо понятие периода или частоты. Однако если затухание мало, то можно условно пользоваться понятием периода как промежутка времени между двумя последующими максимумами (или минимумами) колеблющейся физической величины. Тогда период затухающих колебаний с учетом формулы равен 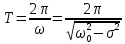 Если 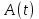 и и 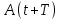 – амплитуды двух последовательных колебаний, соответствующих моментам времени, отличающимся на период, то отношение – амплитуды двух последовательных колебаний, соответствующих моментам времени, отличающимся на период, то отношение 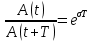 Результаты 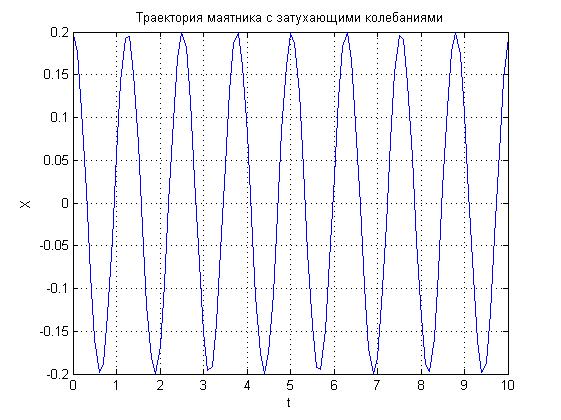  Вывод В данной работе был произведен расчет траектории маятников с затухающими и незатухающими колебаниями. Для написания данной программы был использован язык программирования С++. Результаты расчётов были записаны в файл. После были простроены графики координат маятников от времени с использованием функций Matlab. Полученные результаты согласуются с физическими представлениями об этом явлении. Листинг #include #include #include #include #define M_PI 3.14159265358979323846 using namespace std; int main() { double a0 = 0.2, sig=0.07, s, w=5, fi=M_PI/2, t; ofstream fout; fout.open("Result1.txt"); for (t = 0; t < 10; t+=0.1) { s = a0 * exp(-sig * t) * sin(w * t + fi); fout << t << '\t' << s << '\n'; } fout.open("Result2.txt"); for (t = 0; t < 10; t += 0.1) { s = a0 * sin(w * t + fi); fout << t << '\t' << s << '\n'; } cout << "well done!"; } clc clear all t = load('Result1.txt'); Tx = t(: , 1); Ty = t(: , 2); figure plot(Tx, Ty) grid on title ('Траектория маятника с незатухающими колебаниями'); ylabel('X'); xlabel('t'); t = load('Result2.txt'); Tx = t(: , 1); Ty = t(: , 2); figure plot(Tx, Ty) grid on title ('Траектория маятника с затухающими колебаниями'); ylabel('X'); xlabel('t'); |
