Екстремумы. Отчет о лабораторной работе
 Скачать 1.72 Mb. Скачать 1.72 Mb.
|
|
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ федеральное государственное автономное образовательное учреждение высшего образования «САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ АЭРОКОСМИЧЕСКОГО ПРИБОРОСТРОЕНИЯ» ИНСТИТУТ НЕПРЕРЫВНОГО И ДИСТАНЦИОННОГО ОБРАЗОВАНИЯ
ОЦЕНКА ПРЕПОДАВАТЕЛЬ
РАБОТУ ВЫПОЛНИЛ
Санкт-Петербург 2022 СОДЕРЖАНИЕ1.Задание 3 2.Порядок выполнения работы 3 3.Индивидуальное задание 6 4.Вывод 10 ЗаданиеУстановить у себя на машине надстройку Поиск решения и научиться решать задачи поиска экстремума с ее помощью. Создана новая рабочая книга Excel. Убедилась, что в моей рабочей книге в пункте главного меню Сервис имеется пункт Поиск решения. В качестве основы для решения взята задача линейного программирования (Error: Reference source not found, Error: Reference source not found). Задано количество неизвестных задачи 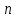 и выделена на рабочем листе Excel группа смежных ячеек для хранения и выделена на рабочем листе Excel группа смежных ячеек для хранения 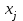 . Эти ячейки обнулены. . Эти ячейки обнулены.На рабочем листе выбрана группа свободных смежных ячеек для хранения коэффициентов 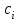 . Заданы значения коэффициентов . Заданы значения коэффициентов 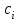 из (Error: Reference source not found) и занесены в соответствующие ячейки. из (Error: Reference source not found) и занесены в соответствующие ячейки. На рабочем листе выбрана свободная ячейка для хранения результатов вычисления целевой функции. Воспользовавшись функцией СУММПРОИЗВ(),в выбранной ячейке запрограммирована формула для вычисления значения целевой функции. Меняя данные в ячейках 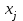 , меняется и значение целевой функции. , меняется и значение целевой функции.На рабочем листе выбрана группа смежных ячеек для хранения коэффициентов 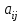 . Заданы значения коэффициентов . Заданы значения коэффициентов 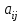 из (Error: Reference source not found) и занесены в соответствующие ячейки. из (Error: Reference source not found) и занесены в соответствующие ячейки. На рабочем листе выделена группа свободных смежных ячеек для хранения коэффициентов 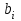 . Заданы значения коэффициентов . Заданы значения коэффициентов 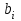 из (Error: Reference source not found) и занесены в соответствующие ячейки. из (Error: Reference source not found) и занесены в соответствующие ячейки. На рабочем листе выбрана группа свободных смежных ячеек для хранения результатов вычисления сумм. 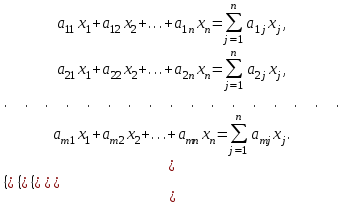 (5). (5). Воспользовавшись функцией СУММПРОИЗВ(), рассчитана в выбранных ячейках значения (5). Меняя данные в ячейках 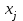 , меняются суммы (5). , меняются суммы (5).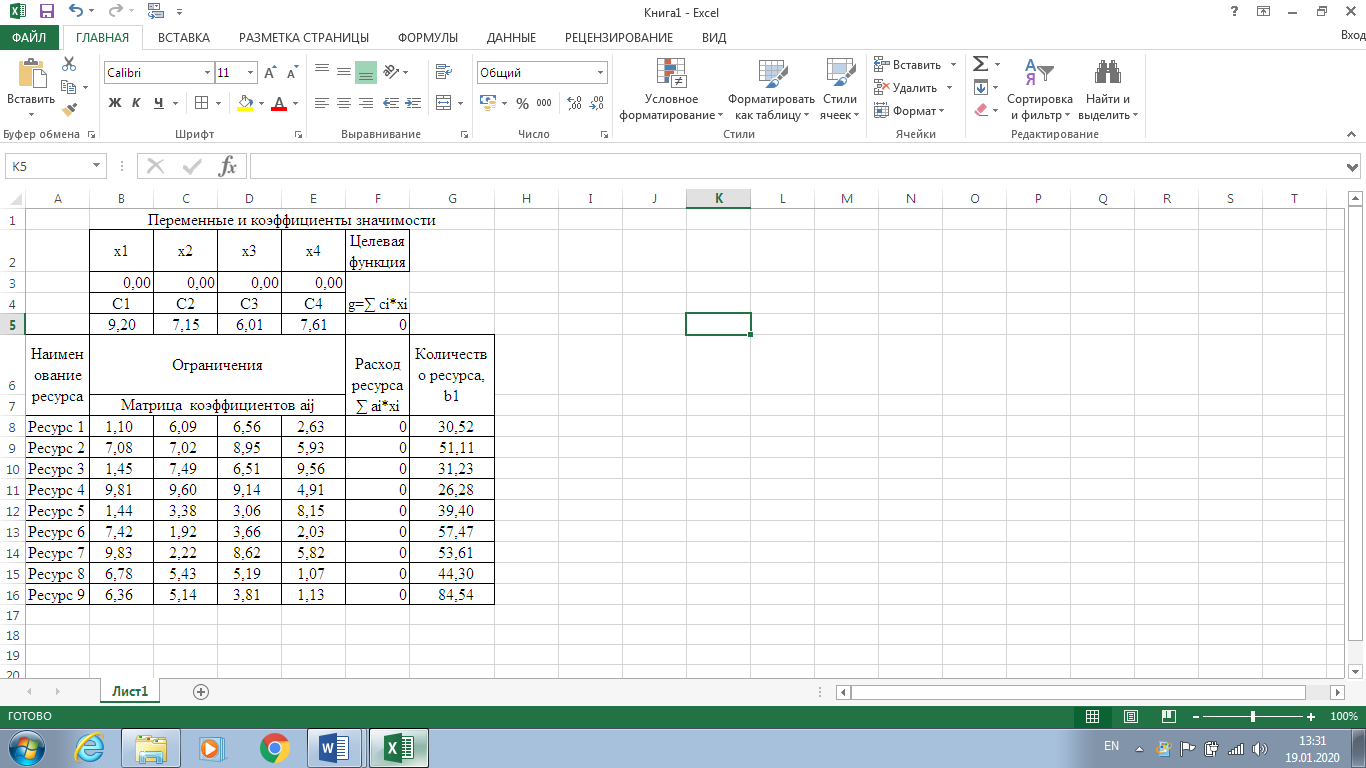 Рисунок 1. Ход работы. Пункты 1- 9 Выполнена команда Поиск решения. Заполнена форма окна в соответствии с заданием. Выполнен переход к форме Параметры поиска решения. Установлен флажок Неотрицательные значения. Нажав кнопку Выполнить получен результат работы надстройки. Диагностическое сообщение - Решение найдено. Все ограничения и условия оптимальности выполнены, заказаны все предлагаемые отчеты. 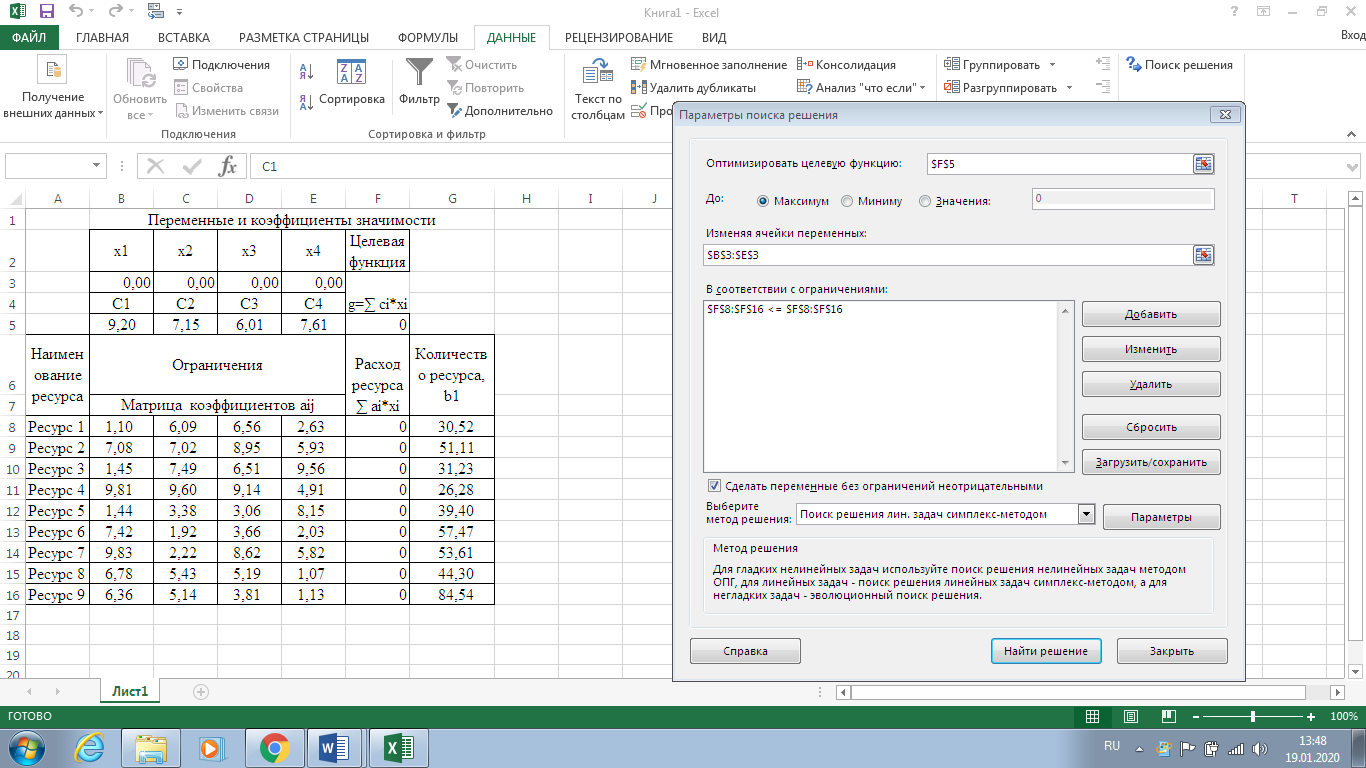 Рисунок 2. Выполнение команды «Поиск решений» 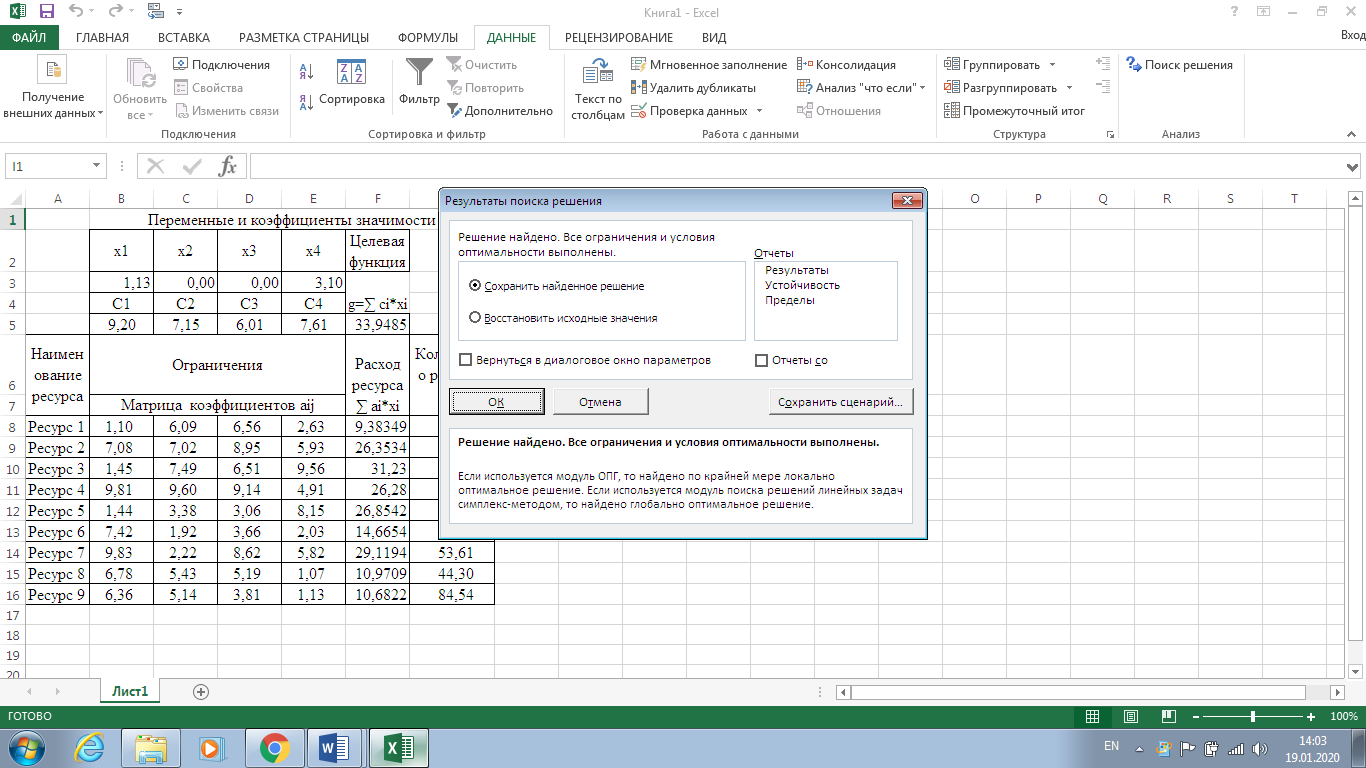 Рисунок 3. Результат поиска решения 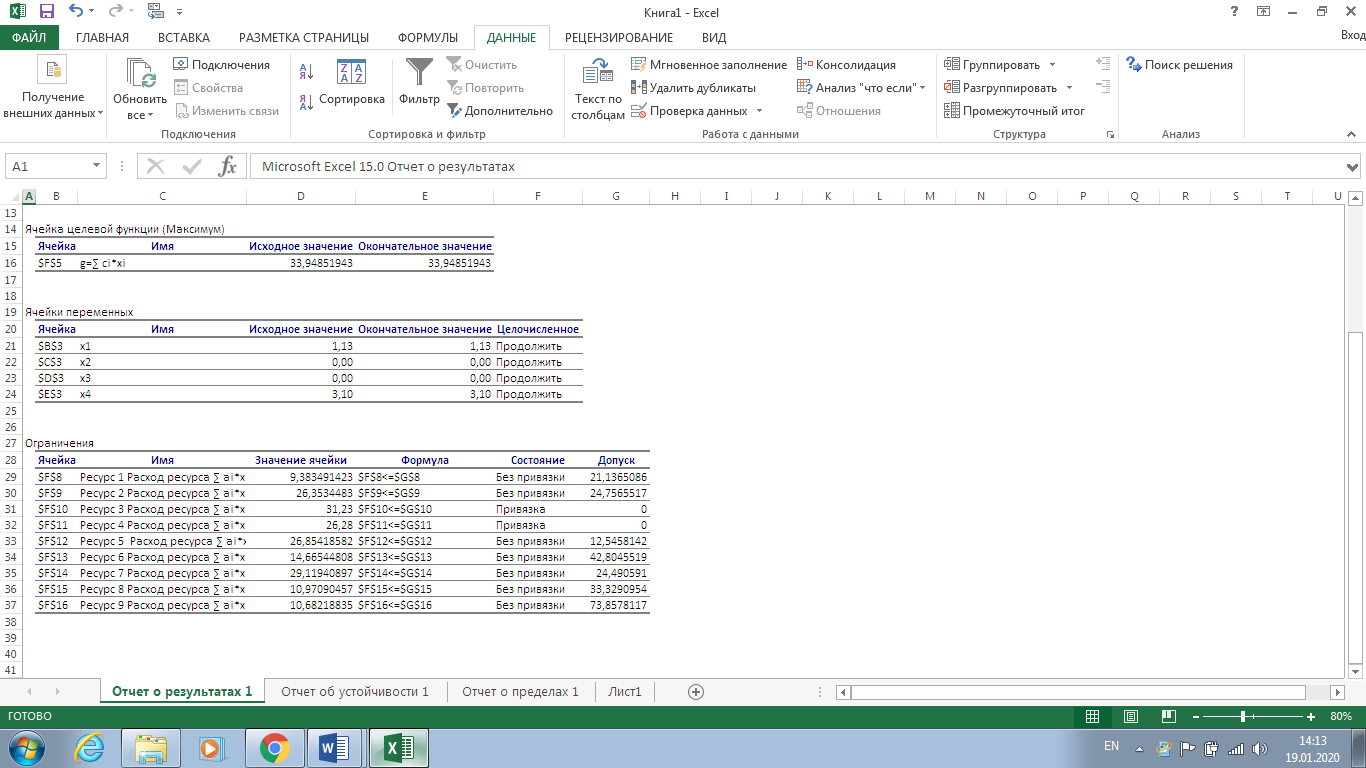 Рисунок 4. Отчёт по результатам 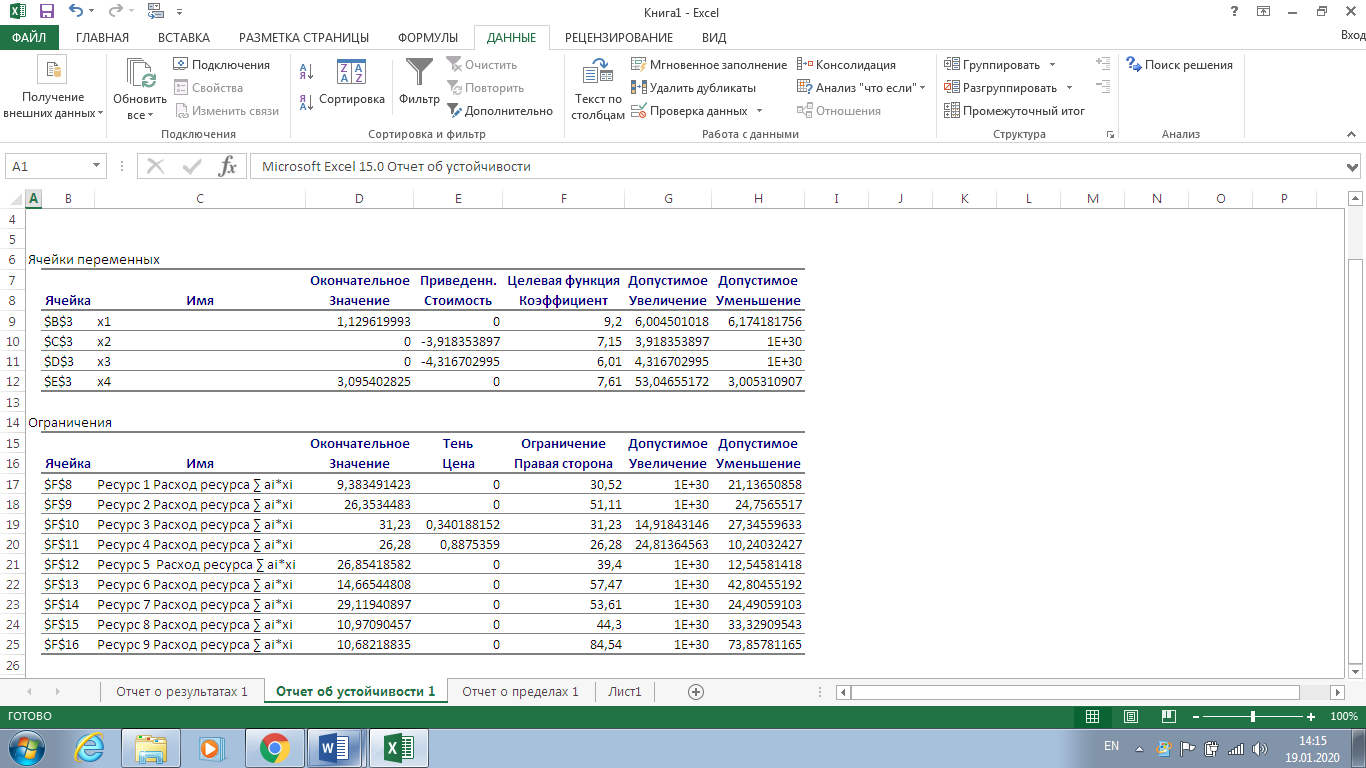 Рисунок 5. Отчёт по устойчивости 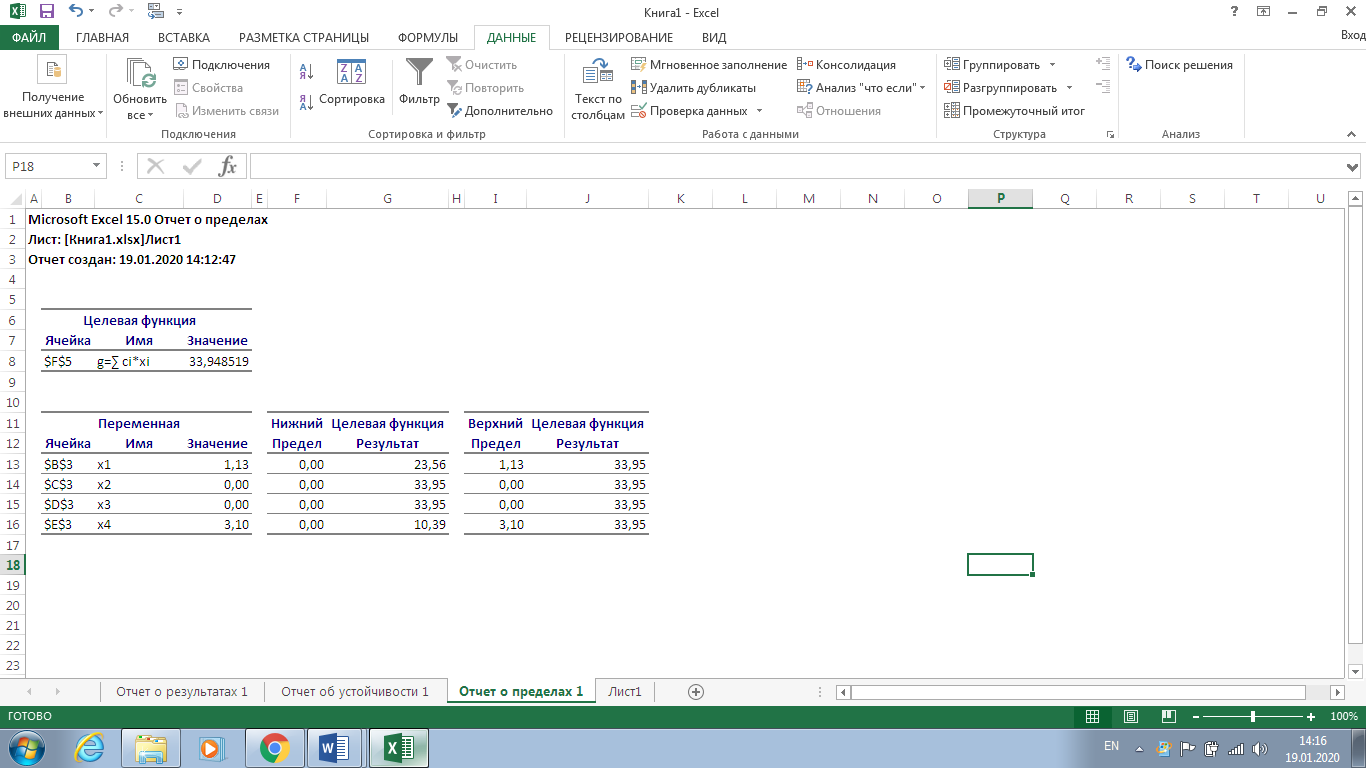 Рисунок 6. Отчёт по пределам Индивидуальное задание
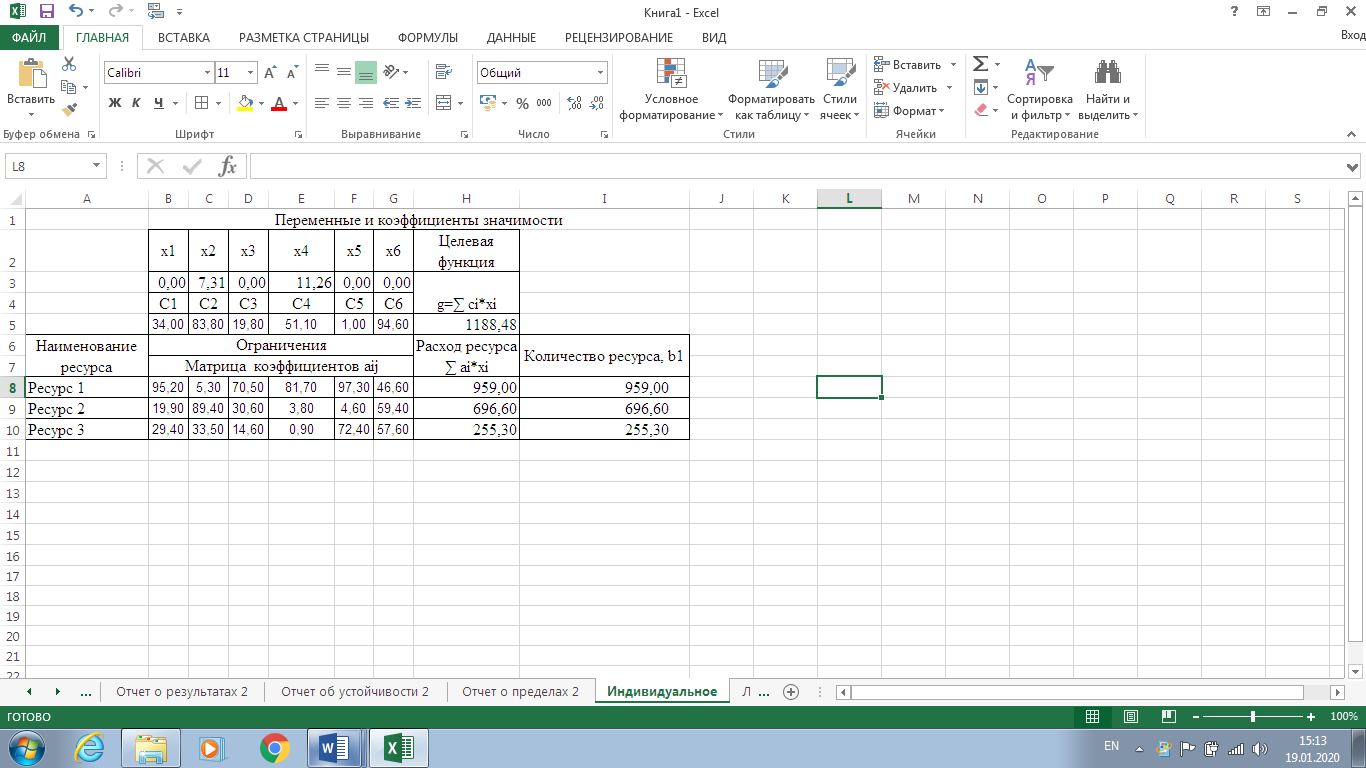 Рисунок 7. Условия индивидуального задания 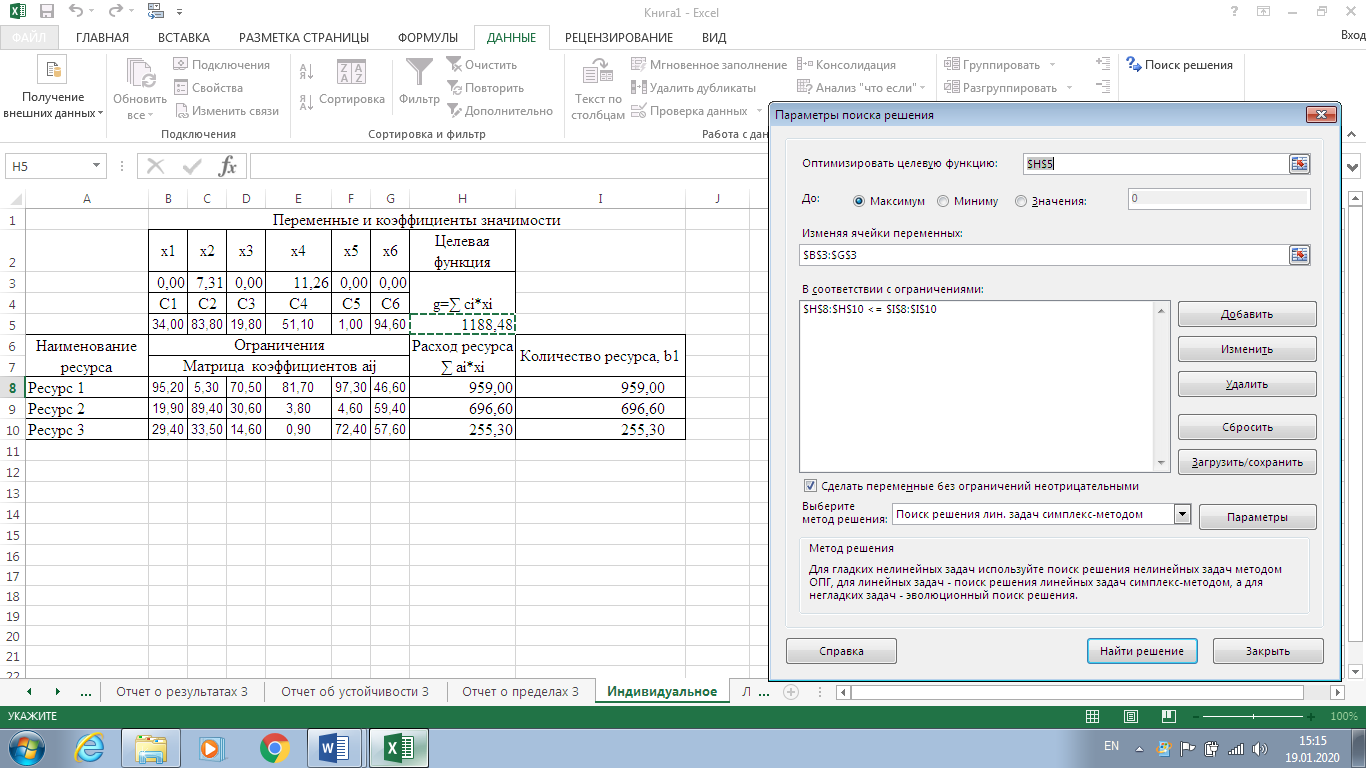 Рисунок 8. Параметры поиска решений индивидуального задания 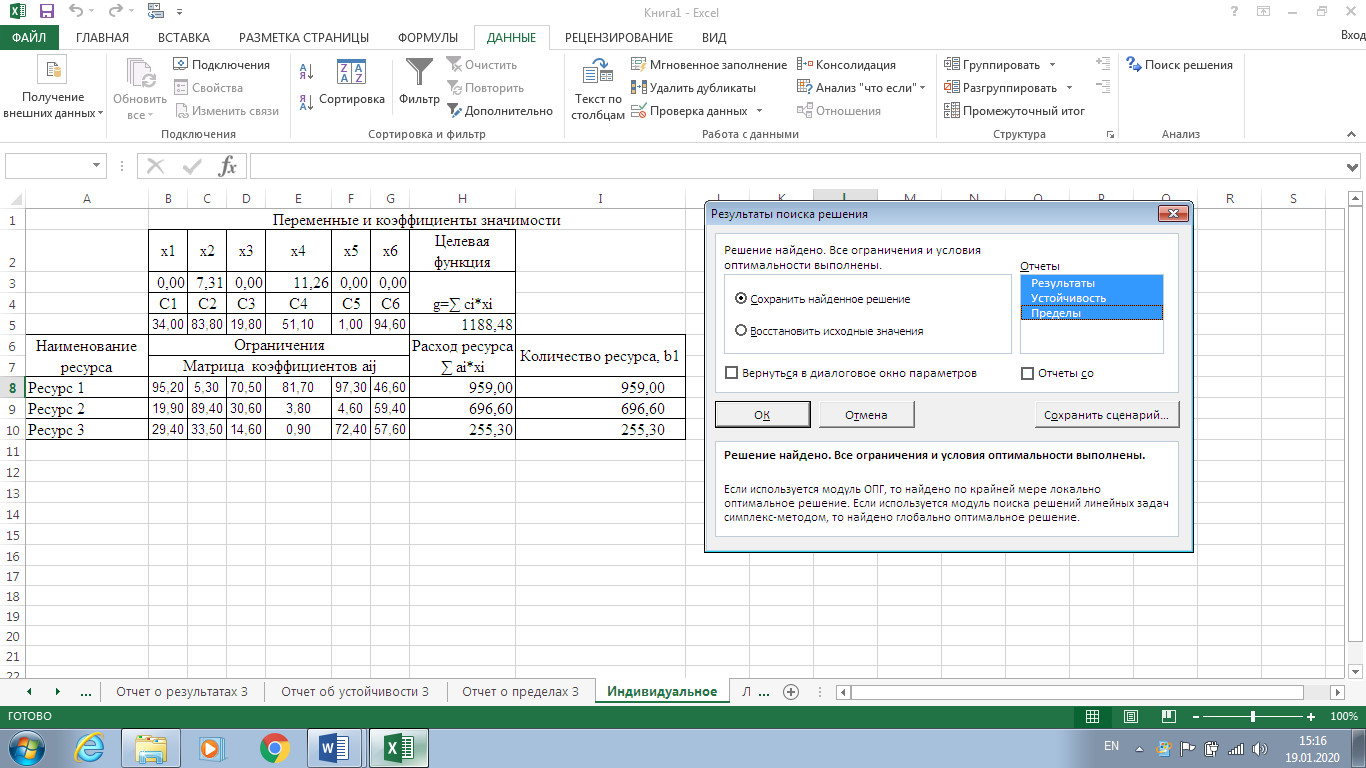 Рисунок 9. Результат поиска решений индивидуального задания Отчет по результатам (рис. 10) содержит начальные (Исходно) и конечные (Результат) значения целевой функции и изменяемых ячеек, а также сводку результатов использования ресурсов. В этой сводке в столбце Статус символами связанное или несвязанное обозначаются соответственно полное или неполное использование соответствующего ресурса. В рассматриваемом примере ресурсы полностью израсходованы. 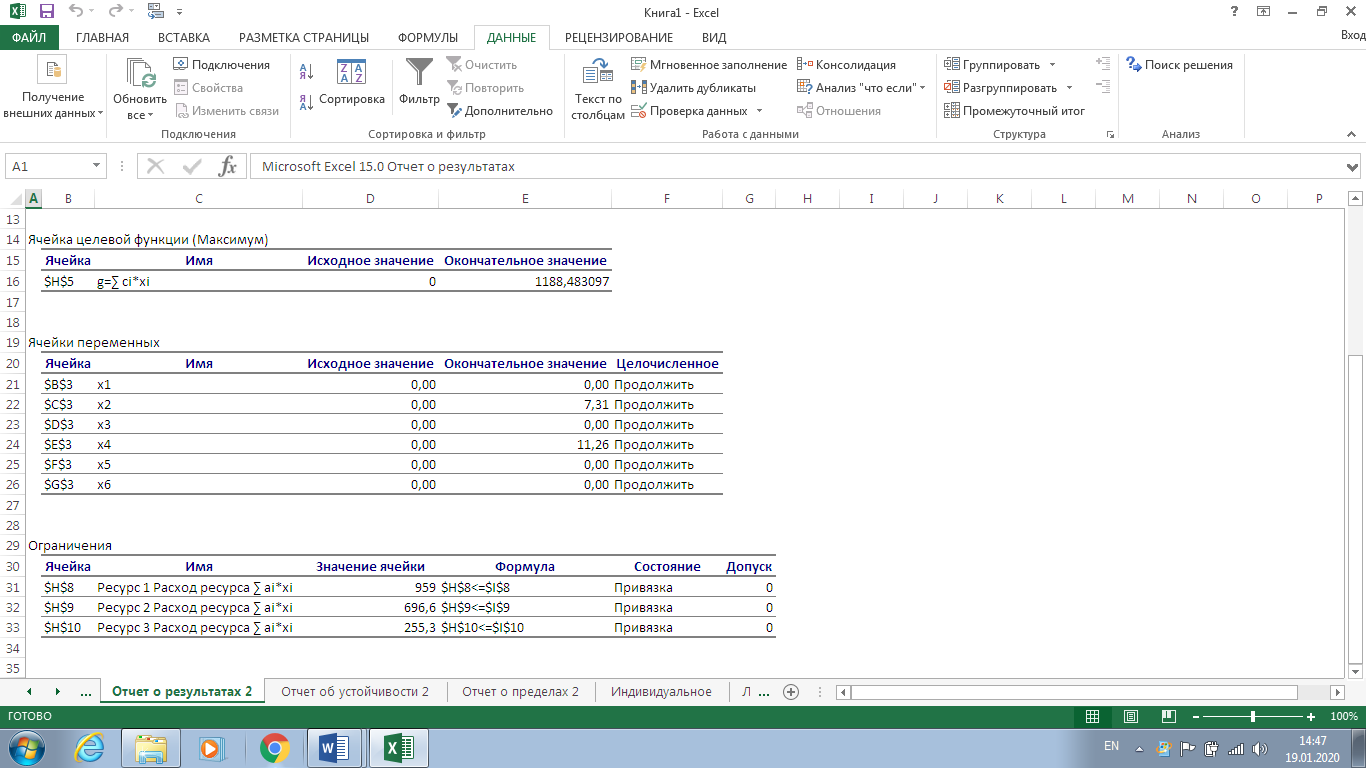 Рисунок 10. Индивидуальное задание. Отчёт по результатам 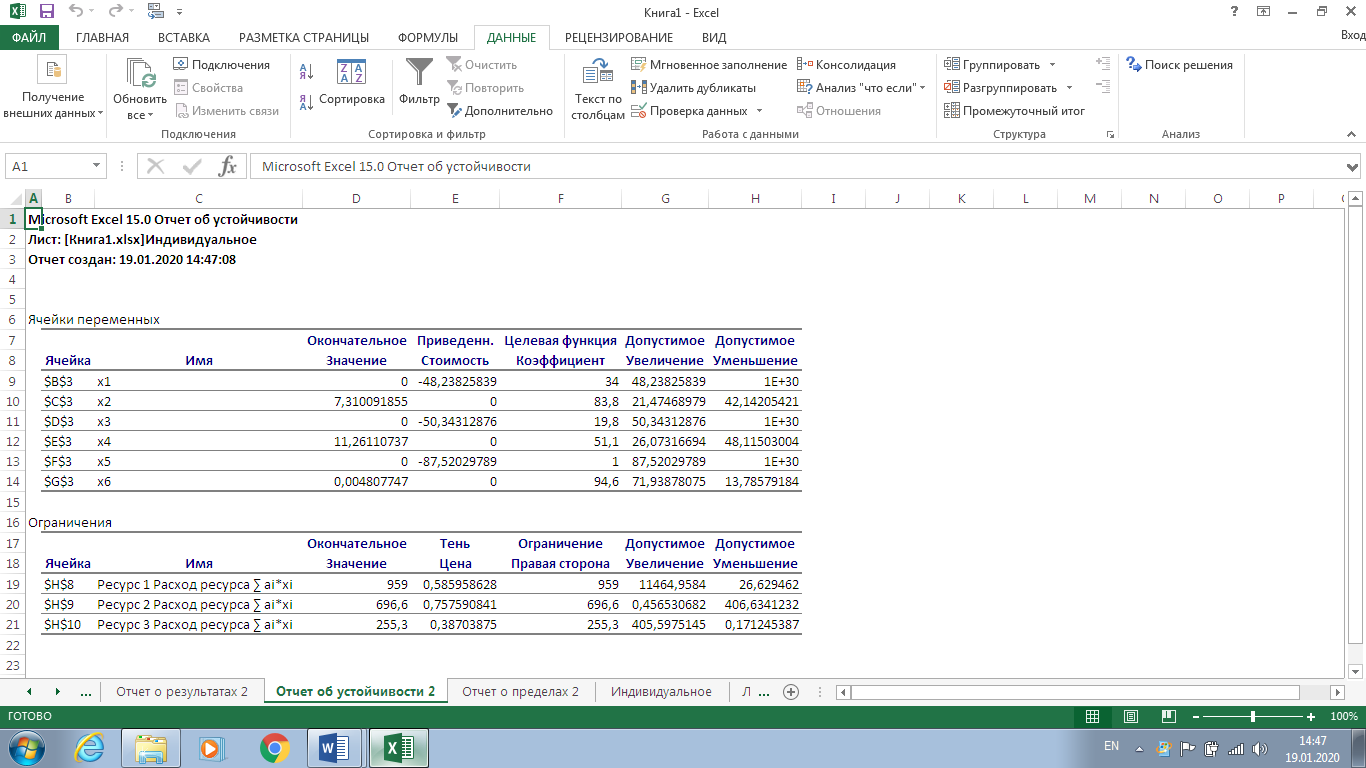 Рисунок 11. Индивидуальное задание. Отчёт по устойчивости Отчет по пределам (рис. 12) показывает возможный диапазон изменения значений переменных, сохраняющий структуру оптимального решения, а также получающиеся в этом случае значения целевой функции. 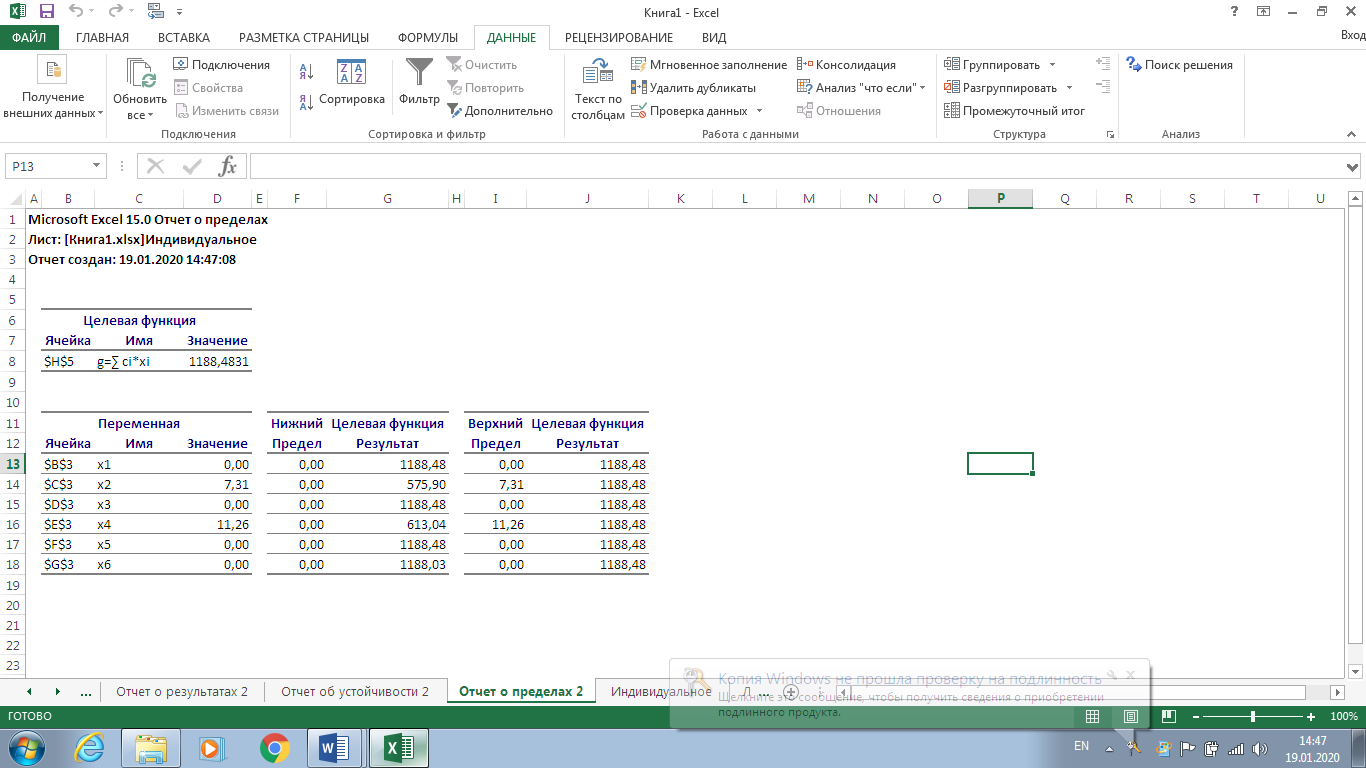 Рисунок 12. Индивидуальное задание. Отчёт по пределам Вернувшись к программируемой задаче, на панели Поиск решения в поле Ограничения нажата кнопка Изменить и на форме Добавление ограничений для выбранных параметров задано дополнительное ограничение Целое = 5,00. Целевая функция значительно уменьшилась. 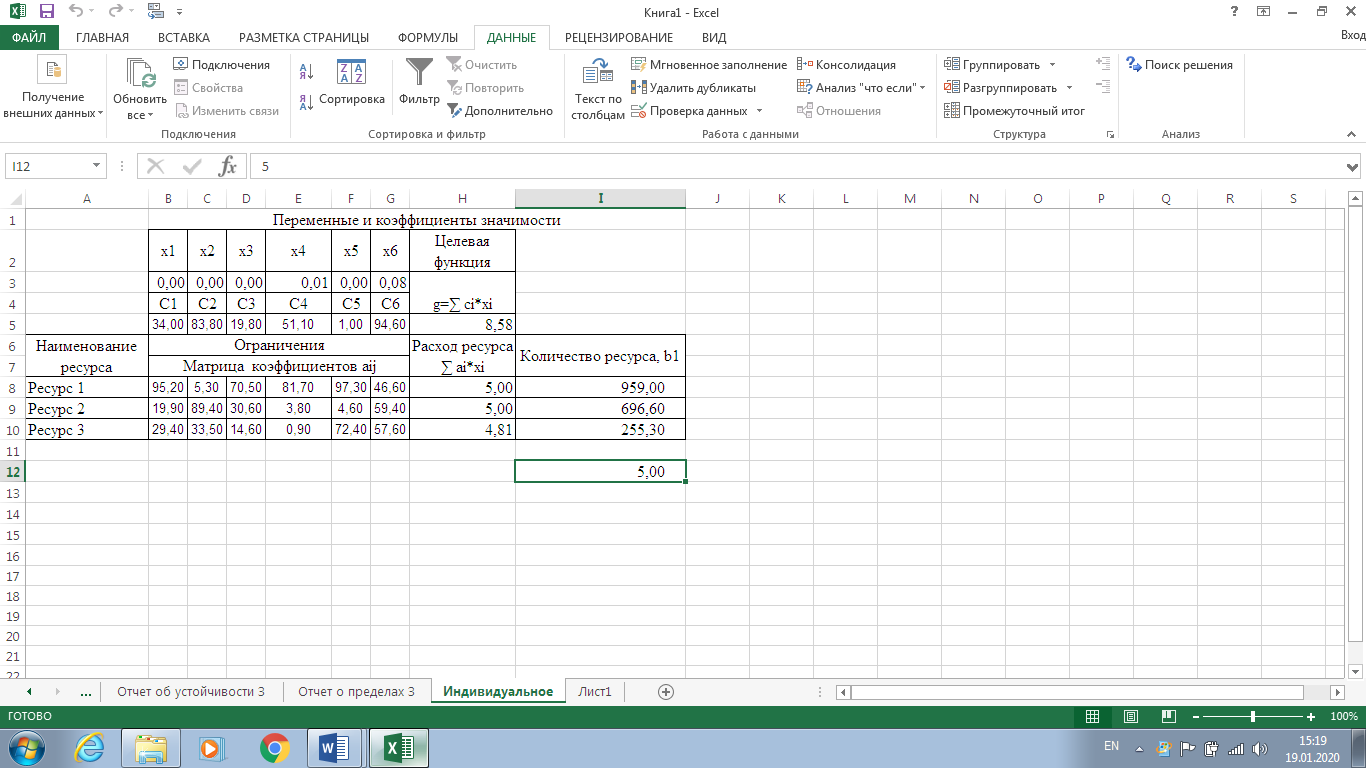 Рисунок 13. Индивидуальное задание с дополнительным ограничением В рассматриваемом примере, при добавлении дополнительного ограничения полностью израсходованы ресурс1, ресурс 2. 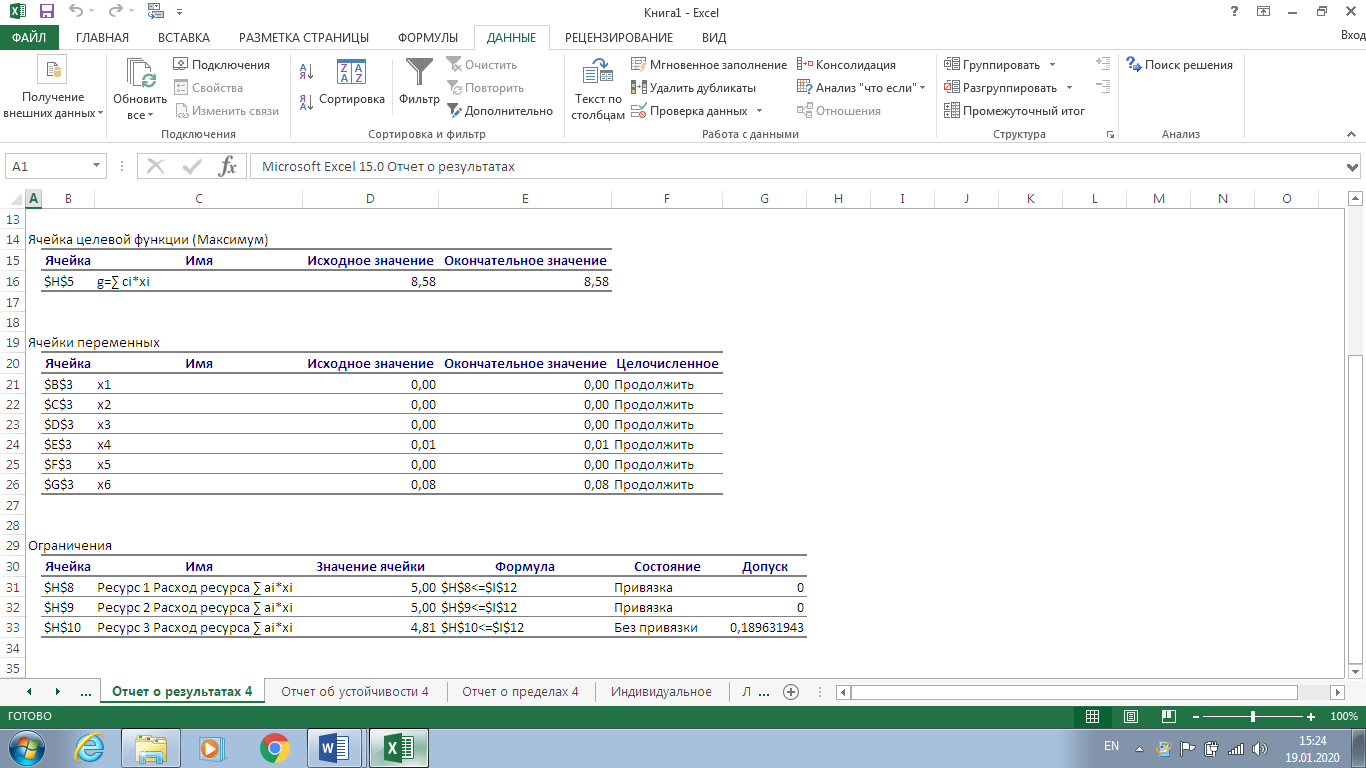 Рисунок 14. Индивидуальное задание с дополнительным ограничением. Отчёт по результатам 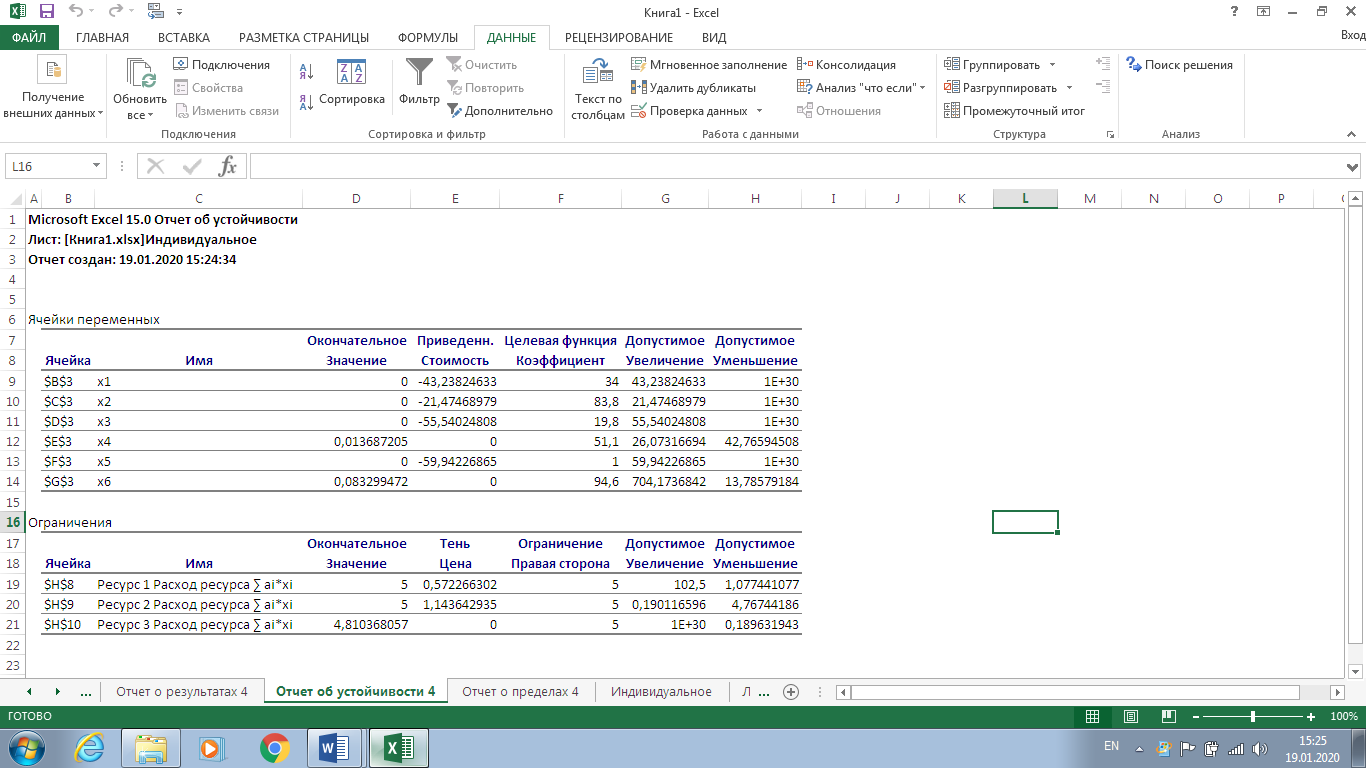 Рисунок 15. Индивидуальное задание с дополнительным ограничением. Отчёт по устойчивости 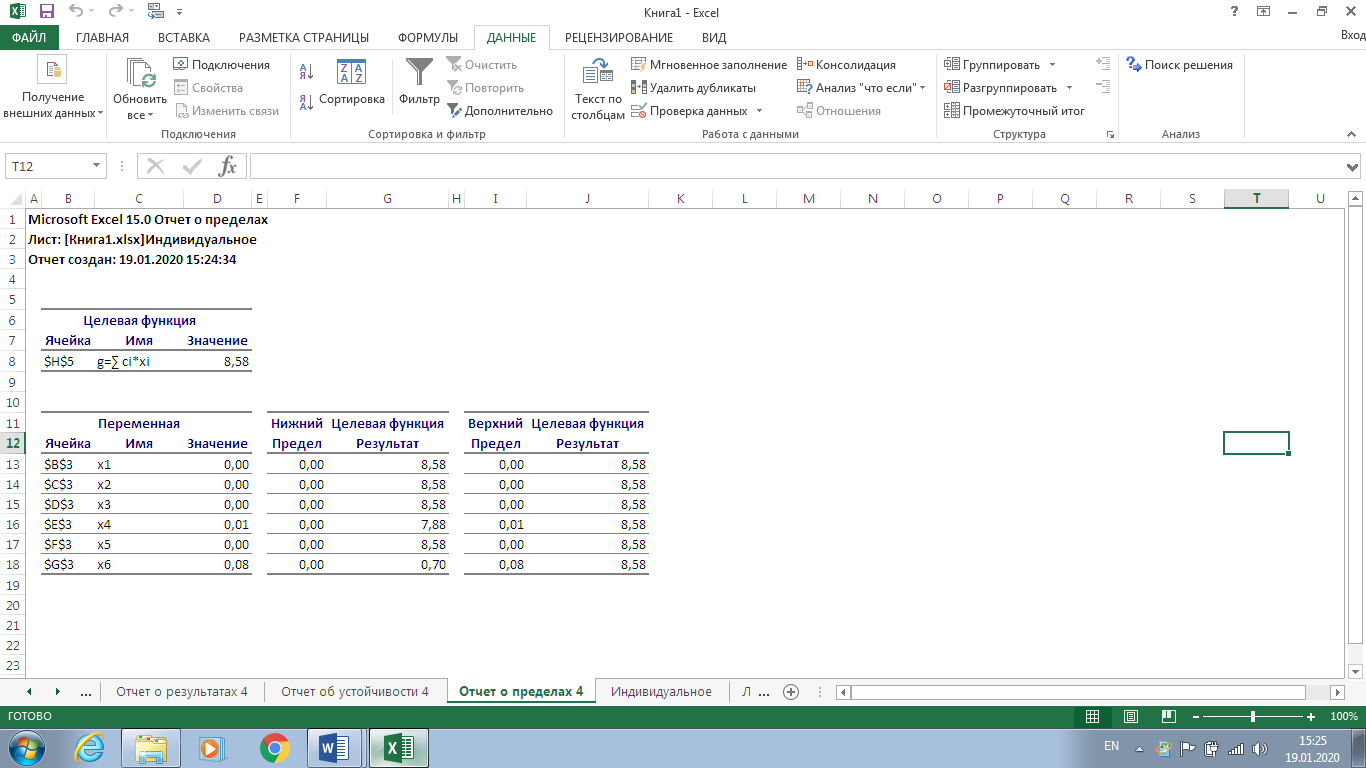 Рисунок 16. Индивидуальное задание с дополнительным ограничением. Отчёт по пределам ВыводРаспространенным методом решения задачи линейного программирования является так называемый симплекс – метод. В его основе лежит так называемая симплекс-таблица, которая составляется по определенным правилам исходя из исходных данных задачи. Доказано, что, производя последовательные преобразования этой таблицы по определенным правилам, можно получить оптимальное решение задачи линейного программирования. Для решения задач поиска экстремума электронные таблицы Excel фирмы Microsoft имеют встроенные средства, оформленные в виде так называемой надстройки. В ходе данной лабораторной работы был получен навык работы с данными надстройками Excel. Решена индивидуальная задача и сгенерировано три отчёта: отчёт по результатам, отчёт по устойчивости, отчёт по пределам. В зависимости от различных вариантов установки ограничения Целое, данные на выходе задачи менялись. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||