Доказательства с нулевым разглашением информации. Отчет Летняя практика 2021 Кулеша. Отчет о производственной практике икит место прохождения практики
 Скачать 67.6 Kb. Скачать 67.6 Kb.
|
|
Федеральное государственное автономное образовательное учреждение высшего образования «СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ» Институт космических и Информационных Технологий Кафедра прикладной математики и компьютерной безопасности ОТЧЕТ О ПРОИЗВОДСТВЕННОЙ ПРАКТИКЕ ИКИТ место прохождения практики Доказательства с нулевым разглашением информации тема Руководитель от университета ________ И.Н. Кирко подпись, дата инициалы, фамилия Студент КИ18-02/1б №031832094 ________ С.В. Кулеша номер группы, зачетной книжки подпись, дата инициалы, фамилия Красноярск 2021 Содержание Список используемых источников 21 ВведениеДоказательство с нулевым разглашением – это интерактивный криптографический протокол, используемый для того, чтобы в двухсторонней коммуникации одна сторона (проверяющий) могла убедиться в достоверности какого-либо утверждения, не имея никакой информации от второй стороны (доказывающей). Таким образом, рассматриваемый протокол требует наличия интерактивных исходных данных от проверяющего, как правило, в виде задачи или проблемы. Цель легального доказывающего (имеющего доказательство) в этом протоколе — убедить проверяющего в том, что у него есть решение, не выдав при этом даже части «секретного» доказательства («нулевое разглашение»). Цель проверяющего же — это удостовериться в том, что доказывающая сторона «не лжёт». ИсторияВ 1986 году в работе Сильвио Микали, Одеда Голдрейха и Ави Вигдерсона было описано применение доказательств с нулевым разглашением для создания криптографических протоколов, которые должны обеспечивать «честное поведение» сторон, сохраняя при этом конфиденциальность. Доказательство с нулевым разглашением было придумано и разработано следующими учёными: Шафи Гольдвассер, Сильвио Микали и Чарльзом Реккофом, и опубликовано ими в статье «Знание и сложность интерактивной системы с доказательством» в 1989 году. Эта работа представила иерархию интерактивных систем с доказательством, основываясь на объёме информации о доказательстве, который необходимо передать от Доказывающего до Проверяющего. Ими так же было предложено первое доказательство конкретно поставленного доказательства с нулевым разглашением — квадратичного вычета по некоторому модулю m. Впоследствии, дополнив свою работу, они были удостоены первой премии Гёделя в 1993 году. В дальнейшем криптосистема Гольдвассер — Микали, основанная на рассматриваемом интерактивном протоколе, являющаяся криптографической системой с открытым ключом, разработанная Шафи Гольдвассер и Сильвио Микали в 1982 году, является первой схемой вероятностного шифрования с открытым ключом, доказуемо стойкая при стандартных криптографических предположениях. Предложенная система была высоко оценена жюри: Гольдовассер и Микали стали лауреатами Премии Тьюринга за 2012 год, за создание криптосистемы с вероятностным шифрованием, отмеченная в номинации как новаторская работа, оказавшая существенное влияние на современную криптографию. Однако, криптосистема является неэффективной, так как порождаемый ею шифротекст может быть в сотни раз длиннее, чем шифруемое сообщение. Для доказательства свойств стойкости криптосистемы Голдвассер и Микали ввели понятие семантической стойкости. В 2021 году Ласло Ловас и Ави Вигдерсон были удостоены Абелевской премии, за их работы в области теоретической информатики, внесшие важнейший вклад в развитие теории сложности вычислений, теории графов, методы распределенных вычислений и концепцию доказательств с нулевым разглашением. Доказательство с нулевым разглашениемДоказательство с нулевым разглашением — интерактивный вероятностный протокол, который позволяет доказать, что доказываемое утверждение верно, и Доказывающий знает это доказательство, в то же время не предоставляя никакой информации о самом доказательстве данного утверждения. Данный криптографический протокол должен обладать тремя свойствами: Полнота: если утверждение действительно верно, то Доказывающий убедит в этом Проверяющего с любой наперед заданной точностью. Корректность: если утверждение неверно, то любой, даже «нечестный», Доказывающий не сможет убедить Проверяющего за исключением пренебрежимо малой вероятности. Нулевое разглашение: если утверждение верно, то любой, даже «нечестный», Проверяющий не узнает ничего кроме самого факта, что утверждение верно. Доказательства с нулевым разглашением не являются доказательствами в математическом смысле этого термина, потому что есть некоторая небольшая вероятность, что обманом доказывающая сторона сможет убедить Проверяющего в ложном утверждении (ошибка корректности). Иными словами, доказательства с нулевым разглашением — это вероятностные доказательства, а не детерминированные. Тем не менее, есть методы, позволяющие уменьшить ошибку корректности до пренебрежимо малых значений. Каждый раунд, или аккредитация доказательства, состоит из трёх этапов. Схематично их можно изобразить следующим образом:   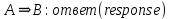 Сначала A выбирает из заранее определённого непустого множества некоторый элемент, который становится её секретом — закрытым ключом. По этому элементу вычисляется, а затем публикуется открытый ключ. Знание секрета определяет множество вопросов, на которые А всегда сможет дать правильные ответы. Затем A выбирает случайный элемент из множества, по определённым правилам (в зависимости от конкретного алгоритма) вычисляет доказательство и затем отсылает его B. После этого B выбирает из всего множества вопросов один и просит A ответить на него (вызов). В зависимости от вопроса, А посылает B ответ. Полученной информации B достаточно, чтобы проверить действительно ли А владеет секретом. Раунды можно повторять сколько угодно раз, пока вероятность того, что A «угадывает» ответы, не станет достаточно низкой. Такой подход называется также «разрезать и выбрать» («cut-and-choose»), впервые использованный в криптографии Михаэлем Рабином. Существует несколько примеров представления протокола: Пещера ненулевого разглашения. Впервые данный пример был написан в хорошо известной работе по доказательству с нулевым разглашением «Как объяснить протокол доказательства с нулевым разглашением вашим детям» Жан-Жаком Кискатером. 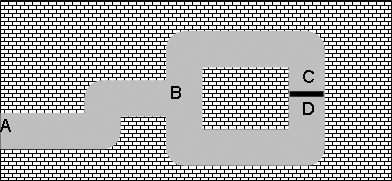 Рисунок 1. Пещера ненулевого разглашения. В данном случае Пегги выступает в качестве Доказывающего утверждение, и Виктор — в качестве Проверяющего (в англоязычной литературе обычно используются наименование сторон Пегги и Виктор (от «Prover» и «Verifier» соответственно). Пегги знает магическое слово («ключ»), ввод которого позволяет открыть ей дверь между C и D. Виктор хочет узнать, действительно ли Пегги знает пароль, при этом Пегги не хочет выдавать сам пароль. Пещера имеет круглую форму, как представлено на рисунке. Для того чтобы решить проблему, они поступают следующим способом. Пока Виктор находится в точке А, Пегги идёт к двери, и после того, как она исчезает из виду, Виктор идёт к разветвлению, то есть в точку B, и кричит оттуда: «Пегги нужно выйти справа» или «Пегги нужно выйти слева». Получаем каждый раз вероятность того, что Пегги не знает пароль, равна 50 %. Если же повторить процесс k раз, то вероятность будет 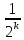 . При 20 же повторениях эта вероятность будет порядка 10−6, что является достаточным для справедливости предположения о том, что Пегги знает ключ. . При 20 же повторениях эта вероятность будет порядка 10−6, что является достаточным для справедливости предположения о том, что Пегги знает ключ.Если Виктор запишет все происходящее на камеру, то полученная видеозапись не будет являться доказательством для какой-либо другой стороны. Ведь они могли заранее сговориться, откуда будет выходить Пегги. Соответственно, она сможет найти выход, не зная при этом самого ключа. Существует ещё один способ: Виктор просто вырезает все неудачные попытки Пегги. Эти описанные выше действия доказывают, что пример с пещерой удовлетворяет свойствам: полноты, корректности и нулевому разглашению. Гамильтонов цикл для больших графов. Этот пример был придуман Мануэлем Блюмом и описан в его работе в 1986 году. Назовём проверяющую сторону Виктор, а доказывающую сторону Пегги. Допустим, Пегги известен гамильтонов цикл в большом графе G. Виктору известен граф G, но он не знает гамильтонова цикла в нём. Пегги хочет доказать Виктору, что она знает гамильтонов цикл, не выдавая при этом ни самого цикла, ни какой-либо информации о нём (возможно Виктор хочет купить информацию об этом гамильтоновом цикле у Пегги, но перед этим желает удостовериться, что Пегги действительно знает его). Для этого Виктор и Пегги совместно выполняют несколько раундов протокола: Вначале Пегги создаёт граф H, изоморфный G. Преобразование гамильтонова цикла между изоморфными графами — тривиальная задача, поэтому если Пегги известен гамильтонов цикл в G, то она также знает гамильтонов цикл в порождаемом графе H. Пегги передаёт граф H Виктору. Виктор выбирает случайный бит 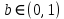 . .Если b = 0, то Виктор просит Пегги доказать изоморфизм G и H, то есть предоставить взаимнооднозначное соответствие вершин этих двух графов. Виктор может проверить, действительно ли G и H изоморфны. Если b = 1, то Виктор просит Пегги указать гамильтонов цикл в H. Для задачи изоморфизма графов на данный момент не доказана ни её принадлежность классу Р, ни её NP-полнота, поэтому будем здесь считать, что невозможно из гамильтонова цикла в H вычислить гамильтонов цикл в изоморфном G. В каждом раунде Виктор выбирает новый случайный бит, который неизвестен Пегги, поэтому, чтобы Пегги могла ответить на оба вопроса, нужно чтобы H был в самом деле изоморфен G, и Пегги должна знать гамильтонов цикл в H (а значит также и в G). Поэтому после достаточного числа раундов, Виктор может быть уверен в том, что у Пегги действительно есть знание о гамильтоновом цикле в G. С другой стороны, Пегги не раскрывает никакой информации о гамильтоновом цикле в G. Более того, Виктору сложно будет доказать кому-либо ещё, что он сам или Пегги знают гамильтонов цикл в G. Предположим, что Пегги неизвестен гамильтонов цикл в G, но она хочет обмануть Виктора. Тогда Пегги необходим неизоморфный G граф G′, в котором она всё-таки знает гамильтонов цикл. В каждом раунде она может передавать Виктору либо H′ — изоморфный G′, либо H — изоморфный G. Если Виктор попросит доказать изоморфизм графов, и ему был передан H, то обман не вскроется. Аналогично, если он просит показать гамильтонов цикл, и ему был передан H′. В таком случае вероятность того, что Пегги всё-таки обманет Виктора после k раундов, равна 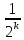 что может быть меньше любой заранее заданной величины при достаточном числе раундов. что может быть меньше любой заранее заданной величины при достаточном числе раундов.Предположим, что Виктор не узнал гамильтонов цикл, но хочет доказать Бобу, что Пегги его знает. Если Виктор, например, заснял на видео все раунды протокола, Боб едва ли ему поверит. Боб может предположить, что Виктор и Пегги в сговоре, и в каждом раунде Виктор заранее сообщал Пегги свой выбор случайного бита, чтобы Пегги могла передавать ему H для проверок изоморфизма и H′ для проверок гамильтонова цикла. Таким образом без участия Пегги доказать, что она знает гамильтонов цикл, можно лишь доказав, что во всех раундах протокола выбирались действительно случайные биты. Уязвимости протоколаКак и любая вещь в нашем мире, доказательство с нулевым разглашением не является идеальным. Ниже я хотел бы разобрать примеры злоупотреблений и атак, основанных на слабых сторонах протокола.  Рисунок 2. Графическое представление проблемы гроссмейстера. П 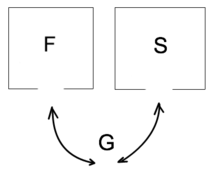 роблема гроссмейстера. Проблема гроссмейстера — один из способов злоупотребления доказательством с нулевым разглашением. Также является одной из задач теории игр. Проблема заключается в том, что злоумышленник может доказать владение секретом, не обладая им на самом деле, или, другими словами, может имитировать то лицо, которому на самом деле принадлежит секрет. Примером данной проблемы является история девочки, которая продемонстрировала одновременную игру против двух гроссмейстеров. Её методика заключалась в следующем: роблема гроссмейстера. Проблема гроссмейстера — один из способов злоупотребления доказательством с нулевым разглашением. Также является одной из задач теории игр. Проблема заключается в том, что злоумышленник может доказать владение секретом, не обладая им на самом деле, или, другими словами, может имитировать то лицо, которому на самом деле принадлежит секрет. Примером данной проблемы является история девочки, которая продемонстрировала одновременную игру против двух гроссмейстеров. Её методика заключалась в следующем: Алиса играет против двух гроссмейстеров, которые находятся в разных комнатах и не знают о присутствии друг друга. Алиса записывает ходы одного гроссмейстера и дублирует их в игре с другим, затем записывает ходы второго и повторяет с первым, и так далее. Таким образом это продолжается до того момента, пока она не проиграет одну партию, выигрывая вторую, или пока обе партии не закончатся вничью. Использование этого обмана позволяет обмануть любого шахматиста и выиграть благодаря не своим знаниям. Гроссмейстеры хотят быть уверены в том, что подобного рода обман не произойдёт и противники будут играть используя только свои знания, без чужой помощи. Для этого все шахматисты будут следовать следующему протоколу: Перед началом игры шахматисты договариваются о каком-то конкретном значении времени t, выраженном в секундах. Также они договариваются кто играет белыми, а кто — черными. Для удобства обозначим начинающего F (от слова first (первый)), а второго S (от слова second (второй)). Каждый игрок имеет свой секундомер. F начинает игру и устанавливает на своем секундомере время z := 0. S запускает секундомер и точно за время t обдумывает и совершает ход. После хода он должен мгновенно установить на секундомере время y := t. F отсчитывает на секундомере время e. Если e – z ≠ t, то F прекращает игру и считает себя обманутым. Протокол завершается. Иначе, в случае победного хода от S, F признает себя поражённым и протокол завершается. Если же ход не победный, то F точно за время t обдумывает и совершает ход. К этому моменту времени у F на секундомере будет время z := e + t. S отсчитывает на секундомере время f. Если f – y ≠ t, то S прекращает играть, поскольку считает себя обманутым и протокол завершается. Иначе, в случае победного хода от F, S признает своё поражение и протокол завершается. Если же ход не победный, то S точно за время t обдумывает и совершает ход. К этому моменту времени у S на часах будет время y := f + t. Перейти к пункту 4. Обман с несколькими личностями. Обман с несколькими личностями — один из способов злоупотребления доказательством с нулевым разглашением для идентификации участника. В доказательствах с нулевым разглашением предполагается, что доказывающая сторона владеет некоторым секретом, который идентифицирует её личность. Секрет доказывающая сторона получает от доверенного центра. Допустим, что при выдаче секрета внешность индивидуума не проверяется, или она не уникальна, или не может быть проверена надлежащим образом. Тогда эта сторона может сгенерировать несколько секретов, записать их в открытый файл доверенного центра, и следовательно у неё будет «несколько личностей». Такая возможность позволяет, например, совершить преступление и безнаказанно скрыться. Пусть сторона создает несколько личностей, одну из которых никогда не использует. Затем, во время совершения преступления сторона идентифицирует себя этой, никогда не используемой личностью. После преступления личность никогда больше не используется. Таким образом, выследить преступника практически невозможно. Простейший способ предотвращения обмана с несколькими личностями предполагает, что доказывающая сторона не может иметь более одной личности. Один из вариантов заключается в предотвращении кражи детей, защищенных от клонирования, и у которых есть уникальный идентификатор, полученный из части их генетического кода. Также, каждый ребенок может получить личность от родителя только при рождении. Однако, в этот момент родитель может создать несколько личностей для ребенка (например, получение более двух свидетельств о рождении). Поэтому, в этом случае, создание уникальной личности основано на доверии. Обман, выполненный мафией. Обман, выполненный мафией, также известный как Mind fraud attack — один из способов злоупотребления доказательством с нулевым разглашением. Впервые данный метод был описан Иво Десмедтом. 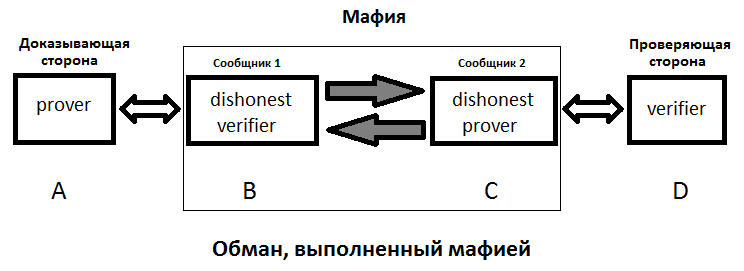 Рисунок 3. Описание проблемы. Пусть имеется 4 участника: A, B, C, D. Причём B и С сотрудничают между собой («принадлежат одной мафии»). А доказывает свою личность B, а С хочет выдать себя за A перед D. Обычно, мошенничество описывают следующей ситуацией: B владеет рестораном, принадлежащим мафии, С — также представитель мафии, D — ювелир. A и D не знают о предстоящем мошенничестве. В момент, когда A готов заплатить за обед и идентифицировать себя перед B, B извещает С о начале мошенничества. Это возможно, благодаря наличию радио-канала между ними. В это время, С выбирает бриллиант, который хочет купить, и D начинает идентифицировать личность С (а на самом деле A). С передаёт вопрос по протоколу B, а тот, в свою очередь, задаёт его А. Ответ передаётся в обратном порядке. Таким образом, А заплатит не только за обед, но и за дорогой бриллиант. Как видно из вышеописанного, существуют определённые требования для подобного мошенничества. Например, моменты, когда А начинает доказывать свою личность перед B, а С — перед D должны быть точно синхронизированы. Обман, выполненный мафией, оказывается действенным в ситуациях, когда нужно совершить атаку на систему, в которой аутентификация является успешной только при условии, что доказывающий участник находится в непосредственной близости от проверяющей стороны, и успешная аутентификация позволяет доказывающему получить некий сервис, предоставляемый проверяющей стороной. Обман, выполненный мафией, широко применяется для атаки на RFID-системы. RFID-система (англ. Radio Frequency IDentification, радиочастотная идентификация) состоит из считывающего устройства (ридера) и транспондера (RFID-метки). Предположим, злоумышленник собирается получить несанкционированный доступ к автомобилю. Доступ обеспечивается посредством RFID (в данном случае транспондером будет бесконтактная карта). Злоумышленник, у которого есть поддельная карта («rogue card»), располагается рядом с автомобилем и устанавливает связь между своей картой и ридером RFID-системы автомобиля («legitimate reader»). В то же время сообщник, обладающий ещё одним считывающим устройством («rogue reader»), находится рядом с владельцем автомобиля и устанавливает соединение с картой легитимного владельца. Таким образом, тот из злоумышленников, кто обладает поддельной картой, передает сообщения, полученные от легитимного ридера, своему подельнику, который пересылает эти сообщения карте (транспондеру) владельца автомобиля. Ответ, полученный с легитимного транспондера, пересылается по той же цепи в обратном направлении и, в конечном итоге, доходит до ридера, установленного на автомобиле. Mafia fraud attack также может применяться для атаки на систему радиолокационного опознавания «Свой-чужой» (IFF — Identification Friend or Foe). Многие IFF-системы используют способ аутентификации «вызов-ответ» («challenge — response authentication»). Например, два самолета W и B могут идентифицировать друг друга посредством IFF, в то время как два вражеских самолета A1 и A2 пытаются выдать себя за «своих». В этом случае применяется схема, аналогичная схеме для атаки на RFID-системы. Например, W посылает запрос A1, для того чтобы он подтвердил свою личность, A1 пересылает сообщение A2, A2 в свою очередь отправляет этот запрос самолету B, который, являясь «своим» для W, отвечает верным сообщением. Данный ответ по тому же пути передается W. Таким образом, W и B будут считать «своими» A1 и A2 соответственно. Техника предотвращения обмана, выполненного мафией, задействующая, так называемые, дистанционно-ограниченные протоколы («distance-bounding protocols»), впервые была приведена в работе Стефана Брандса и Дэйвида Чаума. Данная техника применяется, когда одной из взаимодействующих согласно некоторому криптографическому протоколу сторон необходимо знать, что другой участник находится на расстоянии, не более определенного. Например, если человек применяет электронный пропуск на входе в здание, система аутентификации должна определить, что человек находится от входа на расстоянии, не большем определенного. Согласно Брандсу и Чауму основной элемент дистанционно-ограниченного протокола прост. Он основывается на принципе «вызов-ответ». Происходит k мгновенных обменов битами («rapid bit exchanges») между участниками P и V, P («Prover») — тот, кто доказывает свое знание, V («Verifier») — тот, кто проверяет подлинность того, что доказывает P. Параметр k является секретным параметром протокола. Обмен битами является мгновенным в том смысле, что P после получения бита от V отправлет ответный бит незамедлительно. Основной вид атак, к которой уязвим протокол – атака на основе подобранного шифротекста. Суть такой атаки заключается в том, что криптоаналитик собирает информацию о шифре путём подбора зашифрованного текста и получения его расшифровки при неизвестном ключе. Как правило, криптоаналитик может воспользоваться устройством расшифрования один или несколько раз для получения шифротекста в расшифрованном виде. Используя полученные данные, он может попытаться восстановить секретный ключ для расшифровки. Существуют шифры, для которых атаки данного типа могут оказаться успешными. К их числу относятся: Схема Эль-Гамаля; RSA, используемый в протоколе SSL; NTRU. Для защиты используют шифры RSA-OAEP и Крамера-Шоупа. Атака на основе подобранного шифротекста может быть адаптивной и неадаптивной: при неадаптивной атаке криптоаналитик не использует результаты предыдущих расшифровок, то есть шифротексты подбираются заранее. Такие атаки называют атаками в обеденное время (lunchtime или CCA1), в противоположном случае криптоаналитик адаптивно подбирает шифротекст, который зависит от результатов предыдущих расшифровок (CCA2). В нашем случае данная атака осуществима при использовании неинтерактивного метода взаимодействия в протоколе нулевого разглашения. При использовании такого протокола возникает несколько проблем. Во-первых, нужно решить, как нужно осуществлять взаимодействие, и при этом должны быть сохранены фундаментальные особенности самого протокола: полнота, корректность и «нулевое разглашение». Помимо того, что можно достаточно просто доказать нулевое знание другой стороне, если можно прослушивать канал, то есть столкнуться с проблемой гроссмейстера. Так вот сама атака заключается в следующем: злоумышленник, используя сложность доказательства обладанием знания, включает «атакующий» шифротекст, подсовывая его в кучу других шифротекстов, которые должны быть расшифрованы. Данная атака называется «playback» атака. Возможное решение основано на работе Мони Наора и Моти Юнга, которая заключается в следующем: Доказывающий и Проверяющий шифруют сообщения публичным ключом, это приводит к тому, что описанная выше атака перестает работать. Протокол Фиата-ШамираПротокол Фиата — Шамира — это один из наиболее известных протоколов идентификации с нулевым разглашением. Протокол был предложен Амосом Фиатом и Ади Шамиром. Пусть А знает некоторый секрет s. Необходимо доказать знание этого секрета некоторой стороне В без разглашения какой-либо секретной информации. Стойкость протокола основывается на сложности извлечения квадратного корня по модулю достаточно большого составного числа n, факторизация которого неизвестна. A доказывает B знание s в течение t раундов. Раунд называют также аккредитацией. Каждая аккредитация состоит из 3х этапов. Предварительные действия Доверенный центр Т выбирает и публикует модуль n = p * q, где p, q — простые и держатся в секрете. Каждый претендент A выбирает s взаимно-простое с n, где s ∈ [1, n-1]. Затем вычисляется V = s2. V регистрируется T в качестве открытого ключа A Передаваемые сообщения (этапы каждой аккредитации) 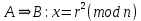 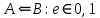 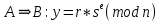 Основные действия Следующие действия последовательно и независимо выполняются t раз. В считает знание доказанным, если все t раундов прошли успешно. А выбирает случайное r, такое, что r ∈ [1, n-1] и отсылает x = r2 (mod n) стороне B (доказательство) B случайно выбирает бит e (e=0 или е=1) и отсылает его A (вызов) А вычисляет у и отправляет его обратно к B. Если e = 0, то y = r, иначе y = r * s (mod n) (ответ) Если y = 0, то B отвергает доказательство или, другими словами, А не удалось доказать знание s. В противном случае, сторона B проверяет, действительно ли y2 = x * ve (mod n) и, если это так, то происходит переход к следующему раунду протокола. Выбор е из множества {0,1} предполагает, что если сторона А действительно знает секрет, то она всегда сможет правильно ответить, вне зависимости от выбранного e. Допустим, что А хочет обмануть B. В этом случае А, может отреагировать только на конкретное значение e. Например, если А знает, что получит е = 0, то А следует действовать строго по инструкции и В примет ответ. В случае, если А знает, что получит е = 1, то А выбирает случайное r и отсылает x = r2 / v на сторону В, в результате получаем нам нужное y = r. Проблема заключается в том, что А изначально не знает какое e он получит и поэтому не может со 100 % вероятностью выслать на сторону В нужные для обмана r и х (x = r2 при e = 0 и x = r2 / v при e = 1). Поэтому вероятность обмана в одном раунде составляет 50%. Чтобы снизить вероятность жульничества (она равна 1/2t) t выбирают достаточно большим (t = 20, t = 40). Таким образом, B удостоверяется в знании А тогда и только тогда, когда все t раундов прошли успешно. Протокол Фейга-Фиата-ШамираПротокол Фейга-Фиата-Шамира — протокол идентификации с нулевым разглашением, обобщение более раннего протокола Фиата — Шамира, разработанный Уриэлем Фейге, Амосом Фиатом и Ади Шамиром в 1986 году. Эта простая для реализации и коммерчески значимая схема была запатентована авторами через год после её разработки. Протокол позволяет одному участнику (доказывающему A) доказать другому участнику (проверяющему B), что он обладает секретной информацией, не раскрывая ни единого бита этой информации. Безопасность протокола основана на сложности извлечения квадратного корня по модулю достаточно большого составного числа n, факторизация которого неизвестна. Существуют некоторые улучшения основной версии протокола, позволяющие уменьшить сложность взаимодействий между участниками или встроить в схему идентификационные данные. A доказывает своё знание секрета s стороне B в течение t раундов, не раскрывая при этом ни одного бита самого секрета. Выбор параметров системы Доверенный центр T публикует большое число n = pq, где p и q — простые числа, которые держатся в секрете. Также выбираются целые числа k и t - параметры безопасности. Генерация секретов для участников Каждый участник выбирает k случайных целых чисел 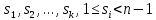 и k случайных бит и k случайных бит 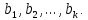 Затем вычисляет 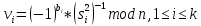 Участник идентифицирует себя окружающим с помощью значений ( 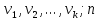 ), которые выступают в качестве его открытого ключа, в то время как секретный ключ ), которые выступают в качестве его открытого ключа, в то время как секретный ключ 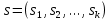 известен только самому участнику. известен только самому участнику.Действия протокола в рамках одного раунда A выбирает случайное целое число 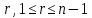 и случайный b; вычисляет и случайный b; вычисляет 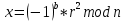 и отправляет x стороне В. и отправляет x стороне В.B отправляет A случайный k-битный вектор 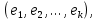 где ei = 0 или ei = 1. где ei = 0 или ei = 1.A вычисляет и отправляет B: 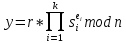 B вычисляет: 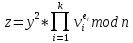 и проверяет, что и проверяет, что 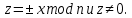 Протокол Гиллу-КискатраПротокол Guillou-Quisquater — это протокол идентификации с нулевым разглашением, расширение более раннего протокола Фиата — Шамира, разработанный Луи Гиллу Жаном-Жаком Кискатр в 1988 году. Протокол позволяет одному участнику (доказывающему A) доказать другому участнику (проверяющему B), что он обладает секретной информацией, не раскрывая ни единого бита этой информации. Безопасность протокола основана на сложности извлечения квадратного корня по модулю достаточно большого составного числа по заданному модулю n. В сравнении с протоколом Фиата-Шамира протокол Гиллу-Кискатра имеет меньшее число сообщений, которыми необходимо поменяться сторонам для идентификации. Протокол требует только один раунд обмена сообщениями, имеет более низкие требования к памяти, используемой для хранения секретов пользователей, однако требует большего объёма вычислений. Кроме того, схему идентификации Гиллу-Кискатра можно легко преобразовать в схему подписи. Сторона A отправляет стороне В свои атрибуты J. Стороне A необходимо убедить сторону В, что это именно её атрибуты. Для этого сторона A доказывает своё знание секрета x стороне B, не раскрывая при этом ни одного бита самого секрета x. Для этого сторонам потребуется всего 1 раунд. Алгоритм создания открытого и закрытого ключей Центр доверия T выбирает два различных случайных простых числа p и q, после чего вычисляет их произведение n = p * q. T выбирает целое число e(1 < e < φ(n)) взаимно простое со значением функции φ(n). Функция φ(n) является функцией Эйлера. T вычисляет s = e-1 mod φ(n) и секрет x = J-s mod n. T вычисляет y = xe mod n. Тройка {n, e, y} публикуется в качестве открытого ключа. x играет роль закрытого ключа, и передается стороне A. Обмен сообщениями А выбирает случайное целое r, находящееся в диапазоне от 1 до n-1. А вычисляет a = re mod n и отправляет его В. В выбирает случайное целое c, находящееся в диапазоне от 0 до e - 1. В посылает c стороне А. А вычисляет z = rxc mod n и посылает его В. B проверяет: если ze = ayc, то подлинность доказана. Эту схему идентификации можно превратить в схему подписи, при этом открытый и закрытый ключи не меняются. Подпись сообщения Пусть А хочет подписать сообщение M. А выбирает случайное целое r, находящееся в диапазоне от 1 до n-1. А вычисляет a = re mod n. А вычисляет d = H(M, a) , где M — подписываемое сообщение, а H(x) — однонаправленная хеш-функция. Значение d, полученное с помощью хеш-функции, должно быть в диапазоне от 0 до e - 1. Если выход хеш-функции выходит за этот диапазон, он должен быть приведен по модулю e. А вычисляет z = rxd mod n. Подпись состоит из сообщения M, двух вычисленных значений d и z, и её атрибутов J. А посылает подпись B. Проверка подписи Пусть В хочет проверить подпись. Тогда, B вычисляет a’ = zeJd mod n. Затем он вычисляет d’ = H(M, a’). Если d = d’, то А знает B, и её подпись действительна. ZK-STARKZK-STARK (Zero-Knowledge Scalable Transparent Argument of Knowledge — «краткий прозрачный аргумент знания с нулевым разглашением») — криптографический протокол, который использует публичные вероятностно проверяемые доказательства с нулевым разглашением. ZK-STARK — прозрачный протокол, то есть не требующий предварительной настройки и раскрытия информации третьей стороне, такие протоколы ещё называют протоколами Артура-Мерлина. Реализация ZK-STARK была предложена в 2018 году профессором Израильского технологического института Эли Бен-Сассоном совместно с Иддо Бентовым, Иином Хорешом и Михаилом Рябцевым. До создания этой технологии для реализации системы с нулевым разглашением повсеместно использовалась технология zk-SNARKs, например, на основе неинтерактивного доказательства с нулевым разглашением (ZK-SNARK) сейчас работает криптовалюта Zcash. Технология ZK-STARK позволяет сильно ускорить процесс обмена информацией и устраняет необходимость предварительной доверительной настройки, что в предыдущих протоколах ставило под угрозу конфеденциальность всей системы. Сейчас новая технология разрабатывается ведущими специалистами компании StarkWare, сооснователем которой является Эли Бен-Сассон. В основе протокола, помимо нулевого разглашения используются принципы аргумента знания и масштабируемости. Аргумент знания — это тип доказательства с нулевым разглашением, в котором доказывается утверждение: «Доказывающий обладает некоторой секретной информацией, которая удовлетворяет некоторой публичной функции». Предположим, что у нас есть публичная функция f, приватная переменная x и публичный результат y. Тогда доказывающая сторона хочет доказать, что она знает такой x, что f(x) = y, без раскрытия x. Стоит отметить, что «аргумент знания» отличается от «доказательства знания» (от англ. Proof of Knowledge), потому что «доказательство знания» — это статистически доказанное утверждение, а «аргумент знания» — вычислительно доказанное утверждение. То есть «доказательство знания» является более сильной конструкцией: доказывающая сторона может обмануть проверяющую «аргументом знания», но не «доказательством знания». Давая определение аргументу знания, мы предположили, что обладаем функцией f. Обычно речь идёт про большую сложность вычисления f(x), тогда краткость алгоритма означает, что процесс верификации проверяющей стороной аргумента знания происходит намного быстрее, чем вычисление f(x). Для ZK-STARK справедливо, что при любом выборе функции f(x) процесс проверки требует экспоненциально меньше времени, чем полное вычисление f(x). Для вычислений, требующих t шагов, необходимо приблизительно O(t log(t)) шагов для создания доказательства. Для верификации необходимо O(t log2(t)) шагов, что даже для больших значений t намного быстрее полного вычисления. Поэтому систему, использующую STARK, называют дважды масштабируемой (от англ. doubly scalable). Стоит отметить, что если мы не оговариваем отдельно нулевое разглашение протокола, то проверяющая сторона может попросить доказывающую сторону просто вычислить значение f(x,y). Технология ZK-STARK позволяет без разглашения секретной информации доказывающей стороной добиться того же результата, что и при использовании протоколов с разглашением, и вдобавок с значимо меньшими затратами по времени. Технология ZK-STARK может быть использована для: Электронного голосования. Тайной верификации, например, для подтверждения личности. Проведения вычислений и проверки результатов вычислений, например для блокчейн транзакций. Авторы алгоритма считают полезным использовать его в том числе для решения проблемы DNA profile match (DPM), то есть для проверки наличия ДНК человека в уже существующих базах данных. Например, для проверки полицией наличия ДНК кандидатов в президенты в криминалистических базах. Таким образом, сгенерированное полицией доказательство не требует раскрытия информации о базах, хранящих ДНК, и о ДНК кандидатов третьим лицам, при этом доказательство публично верифицируемо. Такая проверка проходит быстрее полной сверки образца ДНК со всеми образцами базы данных. Результат проверки: «нет совпадений», «частичное совпадение», «полное совпадение» публикуется и является общедоступным. Сейчас две компании Resistance и StarkWare независимо друг от друга разрабатывают решение для работы децентрализованных бирж на основе технологии ZK-STARK. В StarkWare Industries собираются предложить своё решение для функционирования децентрализованных бирж, а в Resistance планируют запустить собственную биржу на основе ZK-STARKs. Список используемых источниковGoldreich O. A Short Tutorial of Zero-Knowledge // Secure Multi-Party Computation — Amsterdam, Berlin, Tokyo, Washington: IOS Press, 2013. — P. 28—60. — 285 p. Мао В. Современная криптография: Теория и практика / пер. Д. А. Клюшина — М.: Вильямс, 2005. — 768 с. Шнайер Б. Прикладная криптография. Протоколы, алгоритмы, исходные тексты на языке Си = Applied Cryptography. Protocols, Algorithms and Source Code in C. — М.: Триумф, 2002. — 816 с. Blum M. How to Prove a Theorem So No One Else Can Claim It // ICM'86: International Congress of Mathematicians. Berkeley, California, USA, August 3-11, 1986, Proceedings / A. Gleason — Providence: AMS, 1988. — P. 1444—1451. — 1850 p. Desmedt Y. G., Goutier C., Bengio S. Special Uses and Abuses of the Fiat-Shamir Passport Protocol (extended abstract) // Advances in Cryptology — CRYPTO ’87: A Conference on the Theory and Applications of Cryptographic Techniques, Santa Barbara, California, USA, August 16-20, 1987, Proceedings / C. Pomerance — Berlin: Springer Berlin Heidelberg, 1987. — P. 21—39. — (Lecture Notes in Computer Science; Vol. 293) Conway J. H. On Numbers and Games — 111 Fifth Avenue, New York, USA: 1976. Laszl´o Babai. Trading group theory for randomness : — Proceedings of the 17th Annual ACM Symposium on Theory of Computing. — 1985. Fiat A., Shamir A. How to Prove Yourself: Practical Solutions to Identification and Signature Problems // Advances in Cryptology — CRYPTO ’86: 6th Annual International Cryptology Conference, Santa Barbara, California, USA, 1986, Proceedings / A. M. Odlyzko — Springer Berlin Heidelberg, 1987. — P. 186—194. — 490 p. — (Lecture Notes in Computer Science; Vol. 263) Menezes A., van Oorschot P., Vanstone S. Handbook of Applied Cryptography. — CRC Press, 1996. — 816 с. |
