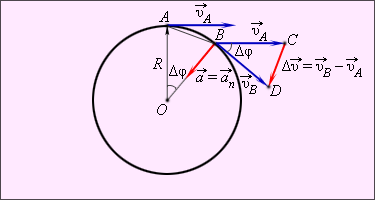
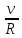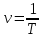ПЛАН УРОКА Движение по окружности - 116. Отчет о выполненной работе преподавателю
 Скачать 327.75 Kb. Скачать 327.75 Kb.
|
Тема: Равномерное движение тела по окружности. Центростремительное ускорение Перечень вопросов, рассматриваемых на уроке: Равномерное движение точки по окружности и его характеристики. Период и частота обращения. Угловая скорость. Центростремительное ускорение. Ответить на вопросы: - При свободном падении движение тела… А) Равномерное. Б) Неравномерное. В) Равноускоренное. Г) Равнозамедленное. Д) Среди ответов правильного нет. - Ускорение свободного падения направлено… А) вертикально вверх при движении тела вверх. Б) Вертикально вниз при падении тела вниз. В) Всегда вертикально вниз. Г) Всегда вертикально вверх. Д) Среди ответов правильного нет. - Шарик падает на землю. Если сопротивление воздуха отсутствует, то скорость шарика… А ) Увеличивается. Б) Уменьшается. В) Остается постоянной. Г) Сначала увеличивается, потом уменьшается. Д) Среди ответов правильного нет. - Тело бросили вертикально вверх. Если сопротивление воздуха отсутствует, то ускорение тела… А) В верхней точке равняется нулю. Б) В верхней точке изменяет направление. В) Увеличивается при падении на землю. Г) Уменьшается при падении на землю. Д) Одинаково на протяжении всего полета. Решение задач. Задача 1. Шарик бросили вертикально вверх. Какие из представленных графиков отвечают движению этого шарика? Сопротивление воздуха отсутствует. h – высота шарика над землей, 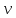 и a – модули скорости и ускорения соответственно… и a – модули скорости и ускорения соответственно…  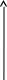 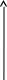 h h 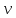 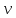 a a            а б в г t t t t А) а; Б)б; В)в; Г)г; Д) среди ответов А-Г правильного нет. Задача 2. Шарик упал на горизонтальную поверхность и, ударившись, подпрыгнул на ту же высоту. Какие из приведенных графиков соответствуют движению этого шарика? Сопротивление воздуха отсутствует. h – высота шарика над землей, 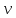 и a – модули скорости и ускорения соответственно… и a – модули скорости и ускорения соответственно…    h h   a a            а б в г t t t t А) а; Б)б; В)в; Г)г; Д) среди ответов А-Г правильного нет. ТЕМА: Равномерное движение тела по окружности. Период и частота обращения. Угловая скорость. Мы уже знакомы с равноускоренным движением. Как же меняются скорость и ускорение при криволинейном движении? Сегодня рассмотрим равномерное движение по окружности, узнаем, что такое центростремительное ускорение. Если траектория движения тела прямая линия, то движение прямолинейное; если траектория кривая линия – криволинейное движение. Напомним, что траектория – это линия, вдоль которой двигалось тело. При изучении равноускоренного движения мы заметили, что в некоторых случаях тело движется по прямой, например свободное падение тел, а в некоторых по кривой – тело, брошенное под углом к горизонту. Рассмотрим движение тела, брошенного под углом к горизонту. Траекторией является парабола. 1. Равномерное движение материальной точки окружности. Линейная скорость. Движение тела по окружности является частным случаем криволинейного движения. Движение, при котором материальная точка движется по окружности с постоянной скоростью, называют равномерным движением по окружности. Допустим, что материальная точка движется равномерно по окружности и в момент t1 находится в положении А (рис. 1), а в момент t2 точка заняла положение В. Радиус, проведенный из центра окружности к материальной точке, за это время описал угол φ, который называют угловым перемещением. Угловое перемещение в международной системе единиц выражают в радианах.  Рисунок 1. Радиан – центральный угол между двумя радиусами окружности, длина дуги между двумя радиусами окружности. Т.е. наряду с вектором перемещения Δl удобно рассматривать угловое перемещение Δφ (или угол поворота), измеряемое в радианах (рис 2). Длина дуги связана с углом поворота соотношением
При малых углах поворота Δl ≈ Δs.
Допустим что материальная точка равномерно движется по окружности радиусом R (рис. 1). Так как движение точки равномерное, то модуль скорости постоянен. Например, за очень малое время  точка переместилась из положения А1 в положение В1 (на рис. 3 для наглядности перемещение А1 В1 показано увеличенным). точка переместилась из положения А1 в положение В1 (на рис. 3 для наглядности перемещение А1 В1 показано увеличенным). Тогда по общему определению скорости линейная скорость на участке направлена вдоль хорды А1 В1. так как хорда при уменьшении промежутка времени  все более приближается к дуге, то вектор скорости в середине участка А1 В1 (в точке С) направлен по касательной к дуге. все более приближается к дуге, то вектор скорости в середине участка А1 В1 (в точке С) направлен по касательной к дуге. 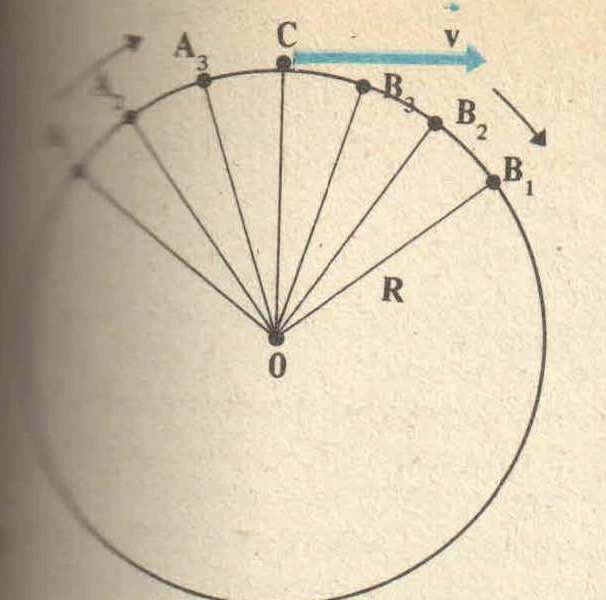 Рисунок 3. Следовательно, и мгновенная скорость в любой другой точке окружности направлена по касательной. В этом можно убедиться, если прижать к вращательному точильному камню конец стального прутка. Раскаленные частицы, отрывающиеся от камня и летящие с той скоростью, которой они обладали в момент отрыва, будут видны в виде искр. Направление вылета искр всегда совпадает с касательной к окружности в той точке, где пруток касается камня, по касательной окружности движутся и брызги от колес буксующего автомобиля (рис 4). Таким образом, линейная скорость тела, движущегося по окружности, оставаясь постоянной по модулю, непрерывно изменяется по направлению и в любой точке направлена по касательной к траектории. Так как модуль линейной скорости постоянен, то его можно определить по формуле 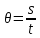 . . За один оборот ( 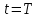 ) тело пройдет расстояние, равное длине окружности: s = 2πR, или , учтя, что Т = ) тело пройдет расстояние, равное длине окружности: s = 2πR, или , учтя, что Т = 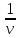 , , 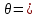 2πR. 2πR.Найдем отношение линейной скорости к угловой: 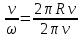 = R. = R. Рисунок 4. Таким образом,
2. Угловая скорость. Угловой скоростью ω тела в данной точке круговой траектории называют отношение углового перемещения Δφ к промежутку времени Δt, в течение которого это перемещение произошло (РИС 2). ω = ∆φ / ∆t Угловая скорость измеряется в рад/с. За единицу угловой скорости в Международной системе единиц принята скорость такого равномерного движения тела по окружности, при котором в каждую секунду совершается угловое перемещение в 1 радиан. Эта единица угловой скорости называется радиан в секунду и обозначается 1 рад/с. Связь между модулем линейной скорости υ и угловой скоростью ω:
При равномерном движении тела по окружности величины υ и ω остаются неизменными. В этом случае при движении изменяется только направление вектора  . . 3. Ускорение при равномерном движении тела по окружности. При равномерном движении тела по окружности его линейная скорость, оставаясь постоянной по модулю, непрерывно изменяется по направлению. Но изменение скорости по направлению свидетельствует о том, что при равномерном движении тела по окружности есть ускорение, которое и является причиной непрерывного изменения направления скорости. Это ускорение получило название центростремительное. По определению ускорение характеризует быстроту изменения скорости и равно отношению изменения скорости к промежуточному времени, за которое это изменение произошло, а его направление совпадает с направлением вектора изменения скорости 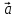 = = 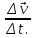 , или в скалярной форме , или в скалярной форме  = = 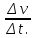 При равномерном движении тела (материальной точки) по окружности ускорение в любой точке траектории перпендикулярно скорости движения и направлено к центру окружности. Модуль его равен частному от деления квадрата линейной скорости на радиус вращения. Итак, равномерное движение тела по окружности является движением с ускорением. Модуль ускорения направлено по радиусу к центру окружности. а = 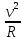 Его называют центростремительным ускорением. Модуль центростремительного ускорения связан с линейной υ и угловой ω скоростями соотношениями: а = 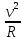 = =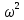 R R При изменении положения тела на окружности изменяется направление скорости и ускорения. При равномерном движении тела по окружности модуль ускорения остается неизменным, но направление вектора ускорения изменяется со временем. При изменении положения тела на окружности изменяется направление скорости и ускорения. При равномерном движении тела по окружности модуль ускорения остается неизменным, но направление вектора ускорения изменяется со временем.
4. Частота и период обращения. Частотой обращения называют число оборотов материальной точки вокруг центра обращения за секунду. Частоту обращения принято обозначать греческой буквой v(ню): 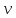 = = 
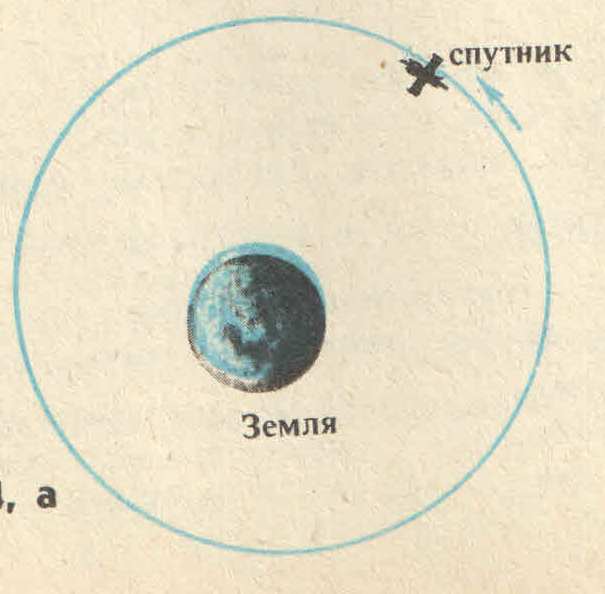  Рисунок 6. Рисунок 7. где  - число оборотов, совершенных за время - число оборотов, совершенных за время  . За единицу частоты в международной системе единиц 1 оборот в секунду. Его сокращенное обозначение – 1 с -1. . За единицу частоты в международной системе единиц 1 оборот в секунду. Его сокращенное обозначение – 1 с -1.Периодом обращения называется время, в течение которого совершается один оборот точки по окружности. Период обозначают буквой Т:
За единицу периода в международной системе единиц принята секунда - 1 с. Нетрудно заметить, что период и частота – величины взаимно обратные:
Закрепление. 1. Решение задач. Задача 1. Определите модуль скорости и центростремительного ускорения точек земной поверхности на экваторе. Радиус Земли принять равным 6400 км. Дано: R = 6400 км = 6,4 . 106 м; Т = 24 ч = 8,64 . 104 с Найти: 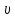 - ? - ?ацс - ? Решение: Точки земной поверхности на экваторе движутся по окружности радиуса R , поэтому модуль их скорости R = 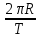 . .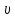 = =   . 102 ≈ 4,65 . 102 = 465 м/с . 102 ≈ 4,65 . 102 = 465 м/с : Центростремительное ускорение можно найти ацс = 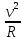 ацс = 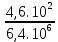 = = 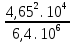 = =  . 10-2 = 3,4 . 10-2 = 0,034 м/с . 10-2 = 3,4 . 10-2 = 0,034 м/сОтвет:= 465 м/с; ацс = 0,034 м/с Задача 2. Велосипедист движется по закруглению дороги радиусом 100 м со скоростью 10 м/с . С каким ускорением он проходит закругление? Дано: R = 100 м; 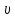 = 10 м/с; = 10 м/с;Найти: ацс = ? Решение: Велосипедист движется равномерно по дуге окружности радиуса R, поэтому возникает центростремительное ускорение, которое можно определить по формуле: ацс = 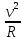 ; ацс = ; ацс = 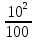 = = 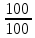 = 1 м/с. = 1 м/с.Ответ: ацс = 1 м/с. Задача 3. Каков радиус кривизны закругления дороги, если по ней автомобиль движется с центростремительным ускорением 2 м/с2 при скорости 72 км/ч? Дано: ацс = 2 м/с2 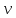 = 72 км/ч = 20 м/с = 72 км/ч = 20 м/сНайти: R = ? Решение: Из формулы центростремительного ускорения определим радиус кривизны закругления дороги: ацс = 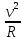 → R = → R =  R = [ R = [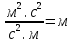 ]. ].R = 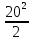 = =  = 200 м = 200 мОтвет: R = 200 м. 6. Подведение итогов урока. Открытый микрофон. «На уроке я узнал (а) о… Особенно интересным было… Не понятным осталось…» 7. Домашнее задание Г.Я.Мякишев, Б.Б.Буховцев, Н.Н.Сотский. Физика, 10 класс, М., «Просвещение», 2016. Читать § 16-17 (с.57-62). Решить задачи 1,2 (с.63). |


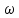 R
R