отчет по статистике. Отчет статистика. Отчет по дисциплине Статистика
 Скачать 120.36 Kb. Скачать 120.36 Kb.
|
|
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ Федеральное государственное образовательное учреждение высшего образования «Тверской государственный технический университет» (ТвГТУ) Кафедра: Бухгалтерский учет и финансы ОТЧЕТ по дисциплине «Статистика» 10 вариант Направление подготовки: 38.03.01 «Экономика» Профиль: «Финансы и кредит» Квалификация (степень) выпускника: бакалавр Форма обучения: заочная Выполнил: Павлова Ю.А курс: 2 группа: Б.ЭК.ФИК.19.68 Проверил: к.т.н Мутовкина Н.Ю Тверь, 2021 Содержание
Задание 1.5 Разработайте макет статистической таблицы, характеризующей зависимость успеваемости студентов группы от посещаемости учебных занятий и занятости внеучебной деятельностью. Сформулируйте заголовок таблицы. Укажите: а) к какому виду относится макет; б) название и вид разработки подлежащего и сказуемого; в) группировочные признаки. Решение:
а) Относительно подлежащего макет относится к виду групповой таблице, относительно сказуемого макет относится к виду сложной таблице. б) Подлежащее - успеваемость; отлично, хорошо, удовлетворительно, неудовлетворительно. Сказуемое ‑ кол‑во студентов; количество посещений учебных занятий, всего, среднее; кол‑во студентов занятых внеучебной деятельностью, среднее, всего. в) По целям и задачам таблица аналитическая. По числу группировочных признаков - простая; По упорядоченности исходных данных – вторичная. Задание 2.10 В задаче дано: объем продаж компании в первом полугодии составил 250 млн. руб. В целом же за год компания планировала реализовать товаров на 600 млн. руб. Вычислите относительный показатель плана на второе полугодие. Решение: Относительный показатель – это обобщающий показатель, который представляет собой результат деления одного абсолютного показателя на другой. Относительный показатель плана (ОПП) - представляет собой отношения планируемого уровня исследуемого процесса на период времени к уровню исследуемого процесса достигнутого в периоде времени.  Согласно условию задачи, объем продаж в первом полугодии составил 250 млн. руб. В целом компания планирует реализовать товар на 600 млн. руб. Следовательно во втором полугодии компания планирует реализовать товара на (600-250=350) 350 млн. руб. Относительный показатель плана реализации товара на второе полугодие равен: 350/250=1,4 Таким образом компания планирует во втором полугодии реализовать на 40% больше товара, чем в первом. Задание 3.10По данным выборочного обследования произведена группировка вкладчиков по размеру вклада в Сбербанке города:
Определите средний размер вклада, используя способ моментов, моду и медиану. Решение Средний размер вклада определяется при помощи формулы: 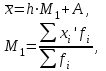 где h - длина интервалов, 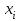 - значение признака у отдельных единиц совокупности, - значение признака у отдельных единиц совокупности, 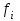 - частота признака, - частота признака,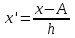 A=  тыс. руб. тыс. руб.Вспомогательные расчеты данного показателя отражены в таблице.
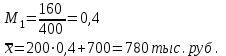 Значение моды определяем по формуле: 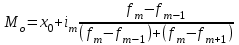 , ,где 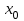 -начало модального интервала (минимальное значение признака в модальном интервале), -начало модального интервала (минимальное значение признака в модальном интервале),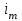 - величина соответственно модального интервала, - величина соответственно модального интервала,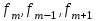 - частота модального, до и послемодального интервалов соответственно. - частота модального, до и послемодального интервалов соответственно.Модальный интервал - интервал с наибольшей частотой признака, в нашей задаче это интервал от 600 до 800 тыс. руб. 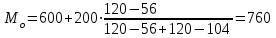 тыс. руб. тыс. руб.Следовательно, чаще всего встречаются вклады размером 760 тыс. руб. Для вычисления медианы в интервальном ряду мы определяем медианный интервал. Для этого производим накопление частот (см. таблицу). Медианным является тот интервал, которому соответствует первая сумма из накопленных частот, в которой содержится половина (или более) суммы всех частот. Поскольку сумма частот равна 400, то тот интервал, в котором находится половина накопленных частот (200). В данной задаче медианным интервалом является интервал со значениями от 600 до 800 тыс. руб. Значение медианы определяем по формуле: 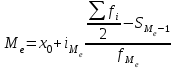 , ,где 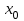 -нижняя граница медианного интервала, -нижняя граница медианного интервала, - величина медианного интервала, - величина медианного интервала, - частота медианного интервала, - частота медианного интервала,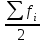 - половина от общего числа наблюдений, - половина от общего числа наблюдений,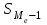 - сумма накопленных частот до начала медианного интервала. - сумма накопленных частот до начала медианного интервала.Получим:  тыс. руб. тыс. руб.Следовательно, половина вкладов в банке открыты на сумму менее 786,667 тыс. руб., а вторая половина – более этой суммы. Задание 4.3По данным выборочного обследования произведена группировка вкладчиков по размеру вклада в Сбербанке города:
Определите: 1) средний размер вклада; 2) среднее линейное отклонение, дисперсию, среднее квадратическое отклонение (используя способ моментов) и коэффициент вариации вкладов. Решение 1) Средний размер вклада определяется при помощи формулы: 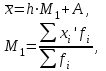 где h - длина интервалов, 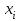 - значение признака у отдельных единиц совокупности, - значение признака у отдельных единиц совокупности, 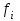 - частота признака, - частота признака,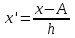 A=  тыс. руб. тыс. руб.Вспомогательные расчеты данного показателя отражены в таблице.
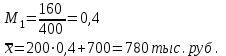 Следовательно, средняя величина вклада составляет 780 тыс. руб. 2) Среднее линейное отклонение: 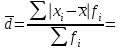 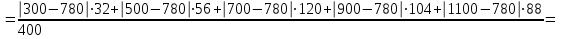 =203,2 тыс. руб. =203,2 тыс. руб.Определим дисперсию методом моментов с помощь формулы: 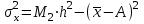 , ,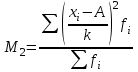 - момент второго порядка. - момент второго порядка.Получим: 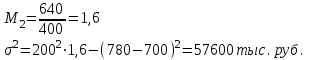 Среднее квадратическое отклонение:  тыс. руб. тыс. руб.Коэффициент вариации: 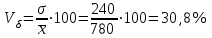 Таким образом, отклонение от среднего размера вклада составляет в среднем 240 тыс. руб. или 30,8%, вариация признака высокая. Задание 5.1За 2010 г. списочная численность рабочих на строительстве объекта составляла на начало месяца, чел.: 01.01 -400, 01.02 -420, 01.03 -405, 01.04 -436, 01.05 -450, 01.06 -472, 01.07-496,01.08-450,01.09-412,01.10- 318,01.11 -231,01.12-235,01.01.03-210. Определите: 1) вид ряда динамики; 2) среднемесячные уровни ряда в I и II полугодиях; 3) изменение списочной численности рабочих на строительстве данного объекта во II полугодии по сравнению с I. Решение 1) Ряд динамики является моментным (данные представлены на определенные даты) и полным (между датами равные промежутки времени). 2) Определим среднюю списочную численность при помощи средней хронологической простой: 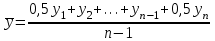 , ,где yi – уровнь ряда на i-ую дату, n – количество временных периодов. Получим: за I полугодие: 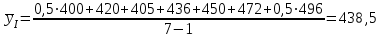 чел. чел.за II полугодие:  чел. чел.Таким образом, средняя списочная численность работников на строительстве объекта составила 439 человек в первом полугодии и 333 человека во втором полугодии. 3) Изменение списочной численности рабочих на строительстве данного объекта во II полугодии по сравнению с I составит: 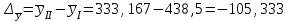 чел. чел.Таким образом, средняя списочная численность работников на строительстве объекта во втором полугодии сократилась на 105 человек по сравнению с первым. Задание 6.10Строительно-производственной деятельности двух СК города характеризуется следующими данными:
Рассчитайте индексы себестоимости переменного и фиксированного составов, а также индекс структурных сдвигов. Объясните результаты расчетов. Решение 1. Индекс динамики себестоимости переменного состава исчисляется по формуле: 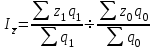 , , где  - себестоимость продукции в отчетном периоде, - себестоимость продукции в отчетном периоде,  - себестоимость продукции в базисном периоде, - себестоимость продукции в базисном периоде,  - количество изделий в отчетном периоде, - количество изделий в отчетном периоде, 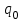 - количество изделий в базисном периоде. - количество изделий в базисном периоде.Составим вспомогательную таблицу:
Получим: 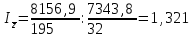 Следовательно, средняя себестоимость выросла на 32,1% под влиянием изменения себестоимости и количества произведенных изделий одновременно. 2. Общий индекс динамики себестоимости фиксированного состава вычисляется по формуле: 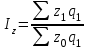 , , он составит: 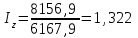 Следовательно, себестоимость выросла на 7,7% под влиянием изменения себестоимости жилья по отдельным строительным организациям. 3. Индекс себестоимости структурных сдвигов:  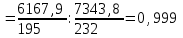 Этот индекс означает, что средняя себестоимость уменьшилась на 0,1% с изменением доли строительных компаний в общем объеме производства жилья. Таким образом, средняя себестоимость жилья в 2010 году выросла на 32,1%, в том числе на 32,2% за счет роста себестоимости по отдельным компаниям и сократилась на 0,1% за счет изменений структуры производства. Задание 7.10Из 100 тыс. семей, проживающих в городе А, методом случайного бесповторного отбора обследовано 2000 семей. Анкеты, посланные семьям, содержали вопрос: живет ли семья в квартире более 10 лет. Из опрошенных семей 600 дали утвердительный ответ. С вероятностью 0.997 определите долю семей в городе А, проживающих в квартире более 10 лет по всей совокупности. Решение Определим выборочную долю семей, проживающих в городе более 10 лет при помощи формулы: 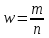 , , где m – численность единиц выборки, обладающих исследуемым признаком, n – суммарная численность единиц выборки (объем выборки). Получим: 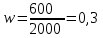 Определим среднюю ошибку выборки:  , ,где w – доля единиц, обладающих исследуемым признаком для выборочной совокупности.  Предельная ошибка для доли: 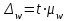 где t – параметр, определяемый при помощи таблиц для заданного уровня Р. При Р=0,997 t=3, отсюда получим: 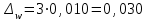 Возможные пределы доли:  0,3-0,030 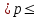 0,3+0,030 0,3+0,0300,270 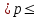 0,330 0,330Таким образом, с вероятностью 99,7% можно утверждать, что доля семей, проживающих в городе более 10 лет, по всему городу составит от 27 до 33%. Список литературыГромыко Г.Л. Теория статистики: практикум. – М., 2016. Сборник задач по теории статистики: Учебное пособие/ Под ред. проф. В.В.Глинского и к.э.н., доц. Л.К.Серга. – Изд.3-е.- М.:ИНФРА-М; Новосибирск: Сибирское соглашение, 2018. Теория статистики: Учебник/ Под ред. проф. Р.А. Шмойловой. - М.: Финансы и статистика, 2017. Толстик Н.В., Матегорина Н.М. Статистика. - Ростов-на-Дону, Феникс, 2016. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
