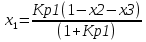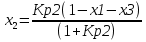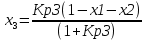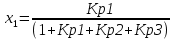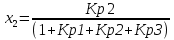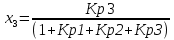Отчет по индивидуальному домашнему заданию 3 по дисциплине Оптимизация химикотехнологических процессов
 Скачать 361.87 Kb. Скачать 361.87 Kb.
|
     МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИФедеральное государственное автономное образовательное учреждение высшего образования НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ ТОМСКИЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ Инженерная школа природных ресурсов Направление подготовки – химическая технология Отделение химической инженерии ОПТИМИЗАЦИЯ ТЕРМОДИНАМИЧЕСКИ РАВНОВЕСНЫХ ХИМИЧЕСКИХ ПРОЦЕССОВ Отчет по индивидуальному домашнему заданию №3 по дисциплине «Оптимизация химико-технологических процессов» Вариант 3 Выполнил студент гр. 2ДМ72 Е.Р. Покоев Проверил старший преподаватель ОХИ А.А. Троян Томск – 2018 Оглавление1 Теоретические сведения 3 1.1 Расчет констант равновесия 3 1.2 Расчет равновесного состава сложных реакций 4 2 Задание 8 3 Алгоритм решения 9 4 Экспериментальная часть 10 10 2-метилпропен 10 10 Kp2 10 10 Kp3 10 10 4.1 Составление материального баланса сложной химической реакции 10 4.2 Составление системы уравнений для расчета неизвестных переменных 11 4.3 Решение системы уравнений 13 4.4 Определение температуры соответствующей максимальному выходу целевых продуктов 16 Выводы 18 Список литературы 19 1 Теоретические сведения1.1 Расчет констант равновесияДля упрощения расчетов во многих термодинамических таблицах приводят величины стандартных энергий Гиббса образования соединений: или логарифмов стандартных констант равновесия образования соединений: Входящая величина 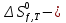 стандартная энтропия образования соединения из элементов при температуре T – вычисляется по уравнению: стандартная энтропия образования соединения из элементов при температуре T – вычисляется по уравнению:По величинам 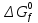 или или 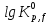 компонентов реагирующей смеси легко найти компонентов реагирующей смеси легко найти 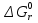 или или 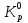 для реакции: для реакции: Стехиометрические коэффициенты в уравнениях берутся со знаком «+» для продуктов реакции и со знаком «-» для исходных реагентов. Зависимость констант равновесия от температуры: 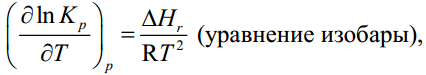 Допуская, что Δ Сp = 0, т.е. Δ Н r,T в небольшом интервале температур остается величиной постоянной и равной Δ Н r,T и Δ Н r, 298, для расчета константы равновесия можно применять уравнения: 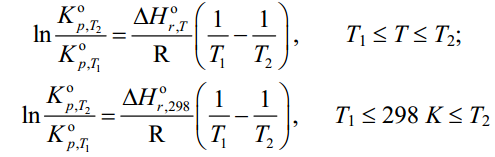 При подстановке в уравнение T1 = 298 К с учетом уравнения изотермы, получим выражение: 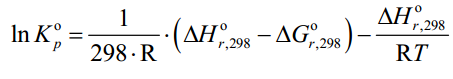 1.2 Расчет равновесного состава сложных реакцийВ подавляющем большинстве реальных процессов органического синтеза одновременно протекают несколько реакций (сложная реакция). Такие процессы характеризуются несколькими стехиометрическими уравнениями и соответственно несколькими константами равновесия. При анализе известной системы сложных реакций, прежде всего, необходимо определить число стехиометрически независимых превращений, уравнения которых нельзя получить комбинацией уравнений других реакций (сложением, вычитанием, умножением стехиометрических коэффициентов на постоянные множители). В большинстве случаев это легко сделать последовательным исключением стехиометрически зависимых реакций. Так при обратимом превращении уравнение обратной реакции легко получить, умножив на минус единицу уравнение прямой реакции. Следовательно, в этом случае имеется только одно независимое превращение. В системе сложных реакций дегидратации этанола: 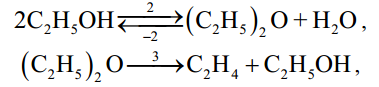 Исключив реакцию -2 (как обратную второй) и реакцию 3 (уравнение которой можно получить вычитанием уравнения 2 из уравнения 1), находим, что система имеет лишь две независимые реакции. В более сложных случаях для определения числа (R) стехиометрически независимых превращений используются методы матричной алгебры. В этом случае составляют стехиометрическую матрицу, строки и столбцы которой соответствуют определенным веществам и реакциям. Для предыдущей системы стехиометрическая матрица будет иметь вид, представленный в таблице 1. Ранг стехиометрической матрицы равен числу независимых реакций. Одновременно с числом независимых реакций определяют равное ему число так называемых ключевых веществ, по которым можно полностью охарактеризовать материальный баланс системы. В простой реакции ключевое вещество только одно. В сложных системах выбор независимых реакций и ключевых веществ взаимосвязан и определяется так, чтобы в каждой независимой реакции участвовало хотя бы одно ключевое вещество и в то же время выбранные ключевые вещества участвовали бы только в одной или в некотором минимуме независимых реакций. Так, для дегидратации этанола выгодно выбрать в качестве независимых реакций - реакции 1 и 2, а в качестве ключевых веществ - этилен и диэтиловый эфир. Выбор ключевых веществ зависит также от простоты и точности их аналитического определения. Таблица 1 – Стехиометрическая матрица сложной реакции 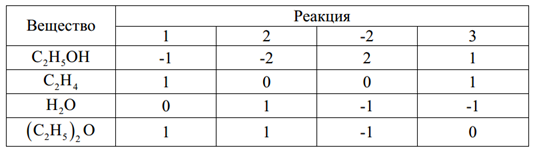 Расчет равновесных концентраций (равновесного состава), удовлетворяющего всем константам равновесия простых реакций можно проводить несколькими способами. В настоящем пособии рассмотрен только традиционный подход к решению задачи нахождения равновесного состава сложной реакции. Если в системе протекает сложная реакция, состоящая из k простых и характеризующаяся таким же числом констант равновесия KN (Kp), а число реагирующих веществ n, то по k уравнениям закона действующих масс и n-k дополнительных уравнений связи между концентрациями (количествами) компонентов можно определить n неизвестных равновесных концентраций.  В случае сложного равновесия теплоты и константы равновесия каждой простой стадии (простой реакции) определяют так же, как если бы в системе протекала только эта реакция. Термодинамический расчет констант равновесия и запись уравнений закона действующих масс не вызывает затруднений. Значительное разнообразие существует в формулировании дополнительных уравнений связи. Наиболее часто используют уравнения стехиометрической зависимости концентраций (количеств) реагирующих компонентов от степени конверсии ключевых веществ и уравнения постоянства числа атомов каждого элемента, входящего в реагирующие вещества. Например, если в молекуле вещества Ai содержится ail атомов l химического элемента и число моль Aiизменяется от ni0 (исходная смесь) до ni (равновесная смесь), то Обычно этих условий достаточно, чтобы получить замкнутую систему уравнений. Например, было установлено, что в сложной реакции риформинга н-гексана протекают 4 независимых реакции: 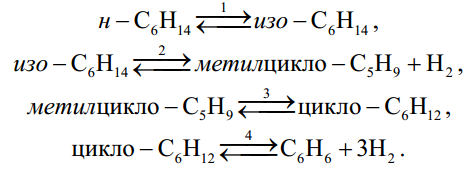 Для этой системы реакций в идеальной газовой смеси имеем 4 уравнения закона действующих масс, в которых 6 неизвестных количеств ni: 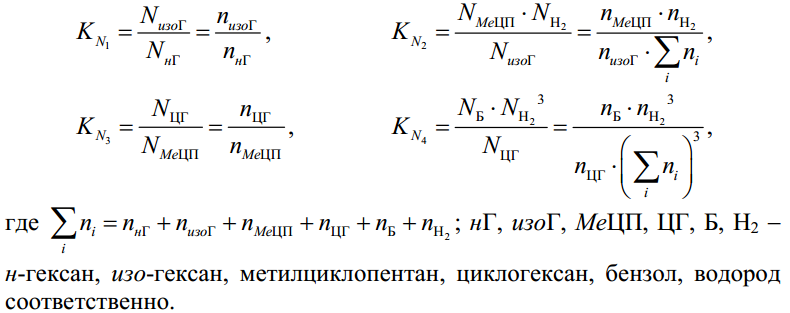 Два дополнительных уравнения получим из условий постоянства чисел атомов C и H. Эти уравнения следующие: 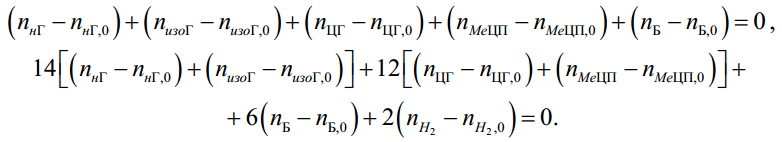 Система равнений с 6 неизвестными является замкнутой (KN1 и ni,0 известны) и имеет единственное решение, имеющее физический смысл. После получения замкнутой системы уравнений возникает задача нахождения решения (степеней превращения, химических переменных, масс компонентов). Нужно отметить, что для однотипных изотермических сложных реакций (изомеризация, алкилирование, диспропорционирование и др.) обычно удается получить аналитические решения. Но если число простых реакций велико, и они относятся к разным типам (например, дегидрирование и изомеризация), а также для адиабатических реакций приходится прибегать к поисковым методам, что требует применения ЭВМ. Поисковые методы, и соответственно методы нахождения равновесных составов по системам уравнений можно разделить на две основные группы: 1) прямой поиск, когда при помощи некоторой итерационной процедуры ищут непосредственно решение системы 2) непрямой поиск, когда используют хорошо разработанные и достаточно универсальные методы нахождения экстремума функции многих переменных Ф; при этом нужно сформулировать такую функцию составов Ф (N1 …, Nn), чтобы равновесный состав N1 …, Nn определял экстремум этой функции. Из прямых методов достаточно часто применяют метод Ньютона-Рафсона. Метод Ньютона-Рафсона хорошо сходится во многих случаях, легко программируется. Он часто входит в стандартное математическое обеспечение современных ЭВМ. Непрямые методы основаны на переходе от решения системы алгебраических уравнений к объединяющей их функции многих переменных. Так, если ввести следующие функции: то минимумам этих функций будет отвечать решение системы алгебраических уравнений: Метод поиска экстремума функции многих переменных хорошо разработан, и их применение оказывается более простым, чем применение прямого метода поиска. 2 Задание 3 Алгоритм решенияАлгоритм решения поставленной задачи состоит из четырех последовательных стадий:
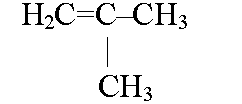
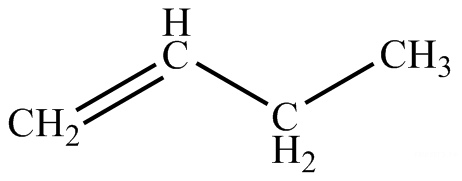
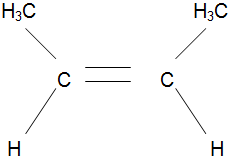
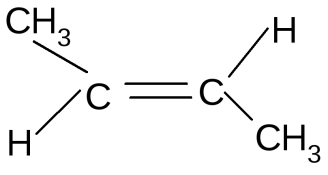
4 Экспериментальная частьУравнения химических реакций, протекающих в реакторе:
4.1 Составление материального баланса сложной химической реакцииПустьx1 – равновесное количество бутена-1, x2 – равновесное количество цис-бутена-2, x3 – равновесное количество цис-бутена-2 равновесное количество транс-бутена-2, p0 – общее давление в системе. Составим материальный баланс (табл.2). Таблица 2 – Материальный баланс сложной равновесной химической реакции.  4.2 Составление системы уравнений для расчета неизвестных переменныхКоэффициенты равновесия исходя из парциальных давлений компонентов смеси (конечный вид выражений): 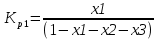 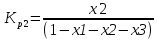 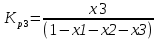 Для решения приведенной системы необходимо определить значения констант равновесия химических реакций. Поскольку таблица со значениями до 1000 К, рассчитываем 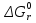 для каждой реакции при интервале температур от 298 до 1100 К при помощи графиков. для каждой реакции при интервале температур от 298 до 1100 К при помощи графиков.Определяем значение констант равновесия исходя из уравнения: 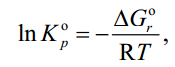 Таблица 3 – Расчет констант равновесия для реакций.  Рисунок 1 – Зависимость константы равновесия первой реакции от температуры. Рисунок 2 – Зависимость константы равновесия второй реакции от температуры. Рисунок 3 – Зависимость константы равновесия третьей реакции от температуры. 4.3 Решение системы уравненийРешение системы нелинейных уравнений производилось в ручную.
4.4 Определение температуры соответствующей максимальному выходу целевых продуктовТаблица 4 – Итоги расчетов.
Рисунок 4 – Зависимость суммарного выхода целевых продуктов цис-бутена-2 и транс-бутена-2 от температуры. Максимальный выход целевых продуктов в исследуемом интервале температур составил 0,429 при температуре 1100ºС. ВыводыВ ходе работы был смоделирован процесс гетерогеннокаталитической изомеризации 2-метилпропена. Определены термодинамические характеристики процесса. Решение системы нелинейных уравнений было осуществлено вручную, ввиду упрощения в ходе решения значения парциального давления системы. Для представленной схемы процесса гетерогеннокаталитической изомеризации 2-метилпропена было определено, что максимальный выход целевых продуктов цис-бутена-2 и транс-бутена-2 составил 0,429 при температуре 1100ºС. Список литературы
|