Контрольная работа (для гр. 31301213). Отчет по контрольной работе должен содержать Титульный лист (образец прилагается ниже) Для
 Скачать 348 Kb. Скачать 348 Kb.
|
106. |
| Component | Ri |
| Parameter | Resistance |
| Start Value | 1 Ом |
| End Value | 1001 Ом |
| Sweep Type | Linear |
| Increment Size | 10 |
| Output node | Точка измерения выходного напряжения |
В поле Sweep for: указать DC Operation point. После заполнения полей нажать кнопку Simulate. В результате моделирования получится зависимость выходного напряжения делителя от сопротивления источника сигнала. Скопировать полученный график и вставить в отчет.
Для отчета нужно также определить, при каком сопротивлении источника сигнала выходное напряжение отличается от идеального на 1%.
Аналогичным образом построить зависимость выходного напряжения от сопротивления нагрузки Rн (RL) со следующими параметрами моделирования:
| Component | RL |
| Parameter | Resistance |
| Start Value | 1 кОм |
| End Value | 1 МОм |
| Sweep Type | Linear |
| Increment Size | 1 кОм |
Скопировать полученный график и вставить в отчет. Для отчета нужно также определить, при каком сопротивлении нагрузки выходное напряжение отличается от идеального на 1%.
Построить зависимости выходного напряжения от сопротивлений R1 и R2 со следующими параметрами моделирования:
| Component | R1 (R2) |
| Parameter | Resistance |
| Start Value | 0.1 кОм |
| End Value | 15 кОм |
| Sweep Type | Linear |
| Increment Size | 0.01 кОм |
Скопировать полученные графики и вставить в отчет.
2. Моделирование ёмкостного делителя.
С помощью программы Workbench 5.0 нужно собрать электрическую схему, изображенную на рис. 2.
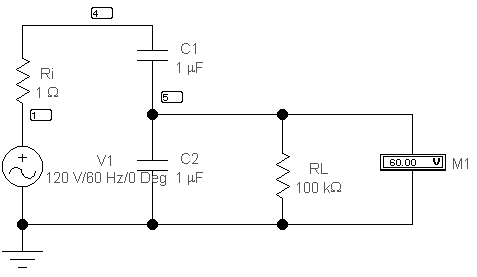
Рис. 2
Для моделирования работы емкостного делителя нужно построить зависимости выходного напряжения делителя от величины емкостей С1и С2, для чего используется моделирование с вариацией параметров2.
Необходимо выбрать пункт меню Analysis/Parameter Sweep. Появится диалоговое окно моделирования с изменением параметров. В полях указать следующие значения:
| Component | С1 (С2) |
| Parameter | Capacity |
| Start Value | 1 μF |
| End Value | 100 μF |
| Sweep Type | Linear |
| Increment Size | 1 μF |
Задав изменение значение емкости C1 в диапазоне 1-100 F c шагом 1, при C2=5 F, запустить процесс моделирования для получения зависимости выходного напряжения делителя от емкости C1.
Для изменения значение емкости конденсаторов необходимо дважды щелкнуть на нужном элементе. Появится окно редактирования свойств, в котором необходимо указать требуемые значения емкости. Выходное напряжение контролировать с помощью вольтметра.
Скопировать полученный график и вставить в отчет.
Задать значение емкости C1 равной 5 F и, изменяя емкость C2 в диапазоне 1-100 F c шагом 1 μF, построить график зависимости выходного напряжения делителя от емкости C2.
Скопировать полученный график и вставить в отчет.
Контрольные вопросы по заданию 1
Что такое масштабное преобразование?
Для чего используются масштабные преобразователи сигналов?
Основные типы масштабных преобразователей.
В каком диапазоне находятся коэффициенты масштабного преобразования для резистивного и емкостного делителей?
Задание 2
1. Цель и задачи задания
Изучить методы создания нелинейных измерительных преобразователей.
Получить практические навыки реализации извлечения квадратного корня методом обратной функции.
2. Теоретическая часть
Содержанием нелинейного измерительного преобразования сигнала является направленное изменение связи между размерами информативных параметров входного и выходного сигнала. Нелинейные измерительные преобразователи (НИП) необходимы для автоматизации косвенных измерений, сжатия данных, например в логарифмическом масштабе, при генерации сигналов сложной формы, при создании функциональных мер и для решения других задач.
Рассмотрим основные методы аналоговых нелинейных измерительных преобразований.
Методы аналоговых нелинейных измерительных преобразований в настоящее время довольно многочисленны (рис. 1). Теоретически каждую функцию можно реализовать многими методами, однако применяются методы, обеспечивающие наиболее рациональную реализацию функции и основывающиеся на использовании естественных физических процессов и устройств, наиболее распространенных при данном уровне техники. В настоящее время большая часть НИП основана на использовании p-n перехода, термоэлектрического эффекта, а также микроэлектронных операционных усилителей для реализации метода обратной функции, умножителей-делителей и делителей для реализации метода неявной функции, электронных интеграторов для реализации различных функций путем интегрирования исходных более просто реализуемых функций. Рассмотрим основные особенности методов создания НИП, реализующих элементарные функции.

Рис. 1 Методы аналоговых нелинейных измерительных преобразований
Метод обратной функции реализуется при помощи компенсационного измерительного преобразователя (рис. 2, а). Если в обратной цепи такого усилителя установлен НИП xk=|у|, то в этой схеме хxk, х=(у), y=-1(xk). Следовательно, в данном устройстве реализуется обратная функция. Смысл обратной функции: последовательное применение любой прямой функции f и обратной к ней функции f1 к аргументу x приводит обратно к этому же аргументу x, т.е. f1f(x)=x.
Естественно, что такой преобразователь целесообразен только в том случае, если заданная функция, xk=(у) воспроизводится проще и может быть использована в цепи обратной связи усилителя. Примером этого служат: электронный логарифматор на усилителе, в цепь обратной связи которого включен экспоненциальный преобразователь на базе p-n перехода, а также корнеизвлекающее устройство, в цепь обратной связи которого включен квадратичный термоэлектрический преобразователь. Метод обратной функции применяется довольно широко, однако он имеет ряд недостатков:
1) возможна реализация только однозначных и монотонных функций, например, arcsin(x) можно воспроизвести только в диапазоне 0.../2;
2) возможно нарушение условий устойчивости и снижение степени подавления погрешности от нестабильности коэффициента усиления прямой цепи, так как коэффициент преобразования обратной цепи изменяется в широком диапазоне значений;
3) при воспроизведении функции извлечения квадратного корня значительно сужается динамический диапазон измерительного прибора.
Метод неявной функции. Метод основан на реализации уравнения, в котором выходная величина преобразователя входит в левую и правую его части
y=f(x,y).
При этом выходная величина y используется и для воздействия на саму себя, т. е. на выходную величину у. Примерами использования метода неявных функций являются:
1) извлечение квадратного корня при помощи делителя (рис. 2, б):

а) для устранения нелинейной зависимости по методу обратной функции; б) для извлечения квадратного корня с помощью делителя по методу неявной функции; в) для определения среднего квадратичного значения; г) для определения разности квадратов двух величин по методу неявной функции.
Рис. 2 Структурные схемы НИП
2) определение среднего квадратического значения (рис. 2, в) с помощью умножителя-делителя:
3) определение геометрической суммы с помощью умножителей-делителей и сумматоров (рис. 2, г).
Нетрудно убедиться, что, решив уравнение
получим
При двух слагаемых сумму можно определить при помощи одного умножителя-делителя и одного сумматора, а при использовании обычной схемы необходимы два квадратора, сумматор и корнеизвлекатель.
4) определение разности двух величин при помощи умножителя-делителя и двух сумматоров (рис. 2, д):
Метод неявной функции имеет следующие преимущества:
1) упрощение структуры при реализации геометрической суммы;
2) отсутствие сужения динамического диапазона при возведении в квадрат;
3) возможность воспроизведения и немонотонных функций, например, функции sin в диапазоне от - до +.
Совместное или раздельное использование методов реализации одной зависимости, указанных на рис. 1, позволяет реализовать: антилогарифмирование, логарифмирование, умножение, деление, извлечение квадратного корня, гиперболический арксинус, гиперболический синус, векторное суммирование, тригонометрические функции и др.
Извлечение квадратного корня. Операция извлечения квадратного корня применяется при измерении среднего квадратичного значения (с.к.з.) сигнала, для линеаризации естественно-квадратичных преобразователей, моделирования различных процессов. Для извлечения квадратного корня применяются квадраторы, например, термоэлектрические преобразователи в обратных преобразователях, логарифматоры по уравнению
а также преобразователи с делителем, реализующие неявную функцию по схеме (рис. 2. б) Uy=KUx.
В НИП, реализующих сложные зависимости, обычно используются полиномиальные модели нелинейности. Для создания НИП, обладающих и высокой точностью, и высоким быстродействием, часто используют гибридизацию аналоговых и кодовых НИП, в частности, в виде НИП на основе дополнительных корректирующих каналов, а также на основе получения полиномиальных зависимостей методом многократного интегрирования.
Для реализации элементарных нелинейных зависимостей можно использовать преобразование различных временных функций, в первую очередь, с помощью интеграторов, а также и дифференциаторов. Например, в электронном интеграторе с последовательным зарядом током Ix=Ux/R за фиксированное время Tц и разрядом током Ib=Ub/R за время Tx до Uc=0 можно реализовать ряд заданных зависимостей Tx=fз(Ux). При этом результат интегрирования вспомогательной функции Ub=f(t) должен быть функцией, обратной заданной. Например, если задана зависимость Tx=KUx, то результат интегрирования должен быть Ux=K1T2x. Этот результат получаем при интегрировании вспомогательной функции Ub=kt. Действительно,
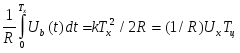 .
.Такой корнеизвлекающий функциональный преобразователь можно использовать для линеаризации квадратичных преобразователей и др.
Если задано
Если задано Tx=ekUx, то результат интегрирования должен быть равен Ux=kln(Tx). Этот результат получаем интегрированием функции Ub=k/t.
3. Практическая часть задания 2
В качестве примера работы нелинейных измерительных преобразователей рассматривается реализация такой операции как извлечение квадратного корня методом обратной функции. Для этого необходимо собрать схему, приведенную на рис. 3

Рис. 3
В свойствах источника V2 и V4 установить коэффициент V1*V1 (E) равным 1 (остальные коэффициенты должны быть равны нулю). В свойствах источника V3 установить коэффициент V1=1 (B) и V2=-1 (C) (E) (остальные коэффициенты должны быть равны нулю).
Для исследования схемы используется моделирование с вариацией параметров3.
Выбрать пункт меню Analysis/Parameter Sweep. Появляется диалоговое окно моделирования с изменением параметров. В полях указать следующие значения:
| Component | V1 |
| Parameter | Voltage |
| Start Value | -99 |
| End Value | 99 |
| Sweep Type | Linear |
| Increment Size | 1 |
| Output node | Выход источника V2 |
В поле Sweep for: указать DC Operation point.
После заполнения полей нажать кнопку Simulate. В результате моделирования получается зависимость выходного напряжения источника V2 от линейно изменяющегося напряжения источника V1.
Скопировать получившуюся зависимость и вставить в отчет.
Аналогичным образом исследовать изменение напряжения на выходе источника V3 от линейно изменяющегося напряжения источника V1.
Скопировать получившуюся зависимость и вставить в отчет.
Контрольные вопросы к заданию 2
Перечислить основные методы создания нелинейных измерительных преобразователей.
Смысл понятия «обратная функция».
Из каких полученных зависимостей видно, что для извлечения квадратного корня используется метод обратной функции?
Какой элемент схемы реализует операцию извлечения квадратного корня?
Задание 3
1. Цель и задачи задания 3
Изучить способы реализации функционального преобразования сигналов.
Получить практические навыки моделирования логарифматора и антилогарифматора.
2. Теоретическая часть
Антилогарифматоры. Для выполнения операции антилогарифмирования используется нелинейность вольт-амперной характеристики p-n перехода.
Для практической реализации антилогарифмической зависимости используется схема (рис. 1, а, б), в которой полупроводниковый диод подключен ко входу операционного усилителя. Тогда
где U0=I0Rос выходное напряжение при Uвх=0; U1 – входное напряжение при Uвых=еU0; Rос – сопротивление обратной связи.

Рис.1 Схема антилогарифматора
Антилогарифмические преобразователи обычно применяют вместе с логарифмическими, например, для операций умножения, деления, возведения в степень.
Логарифматоры. Для реализации логарифмирования на интегральных элементах используются естественная антилогарифмическая зависимость p-n перехода и возможность получения обратной зависимости при помощи усилителя с глубокой отрицательной обратной связью. В схеме логарифматора (рис. 2, а, б) диод располагается в цепи обратной связи.
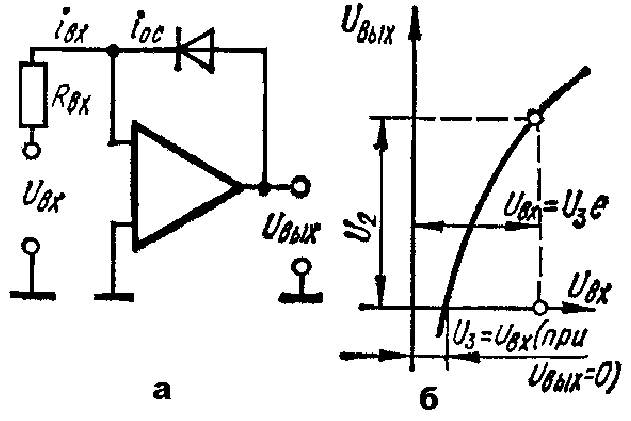
Рис. 2 Схема логарифматора
В этом случае выходное напряжение операционного усилителя оказывается пропорциональным логарифму входного напряжения
где U2 – выходное напряжение при Uвx=eU3;U3 – входное напряжение, при котором выходное напряжение Uвых=0.
Точно реализуемое логарифмирование широко используется:
1) в интегральных умножителях;
2) при воспроизведении полиномов, степенных и показательных функций;
3) при измерении относительных величин в логарифмических единицах;
4) при сжатии динамического диапазона сигнала перед преобразованием или передачей на расстояние;
5) в точных интегральных делителях при широком динамическом диапазоне изменения делимого и делителя.
3. Практическая часть
Для моделирования антилогарифматора и логарифматора с помощью программы Workbench 5.0 необходимо нарисовать схему, приведенную на рис. 3
На операционном усилителе DA1 собрана схема антилогарифматора, а на DA2 – логарифматора.

Рис. 3
Для исследования логарифмических и антилогарифмических характеристик преобразователей используется моделирование с вариацией параметров4.
Нужно получить зависимость выходного напряжения антилогарифматора от линейно изменяющегося входного напряжения.
Для этого нужно выбрать пункт меню Analysis/ Parameter Sweep. Появится диалоговое окно моделирования с изменением параметров. В полях указать следующие значения:
| Component | V1 |
| Parameter | Voltage |
| Start Value | 0 |
| End Value | 0.88 V |
| Sweep Type | Linear |
| Increment Size | 0.01 V |
| Output node | Выход DA1 |
В поле Sweep for: указать DC Operation point.
После заполнения полей нажать кнопку Simulate. В результате моделирования получается зависимость выходного напряжения антилогарифматора от линейно изменяющегося входного напряжения.
Скопировать полученную зависимость и вставить в отчет.
Аналогичным образом исследовать изменение напряжения на выходе логарифматора от линейно изменяющегося входного напряжения при следующих условиях моделирования:
| Component | V1 |
| Parameter | Voltage |
| Start Value | 0 |
| End Value | 13 V |
| Sweep Type | Linear |
| Increment Size | 0.1 V |
| Output node | Выход DA2 |
Скопировать полученную зависимость и вставить в отчет.
Контрольные вопросы по заданию 3
Что такое функциональное преобразование сигналов?
Перечислить основные методы создания нелинейных измерительных преобразователей.
Чем отличается функциональное преобразование сигнала от его масштабного преобразования?
Какой элемент (или элементы) схемы обеспечивает(ют) реализацию логарифмической и антилогарифмической зависимостей?
Задание 4
1. Цель и задачи задания
Изучить метод проведения спектрального анализа сигналов методом разложения в ряд Фурье.
Получить практические навыки разложения простейших периодических функций в спектр с помощью программы Workbench 5.0.
2. Теоретическая часть
В инженерной практике необходимо уметь «проводить» сложные детерминированные и квазидетерминированные сигналы через различные звенья измерительных устройств, а также генерировать такие сигналы. Эти задачи обычно решаются проще, если сложный сигнал можно представить в виде суммы элементарных.
Разложение сложного сигнала на элементарные, производится по определенной системе, в частности по системе ортогональных функций – в обобщенный ряд Фурье
где
Ортогональной называется совокупность функций Сk(t), удовлетворяющая следующему условию на отрезке времени (t2-t1):
 ,
,где k=1, 2, 3, ..., m; n=1, 2, 3, ..., m при nк.
Ортогональность двух функций означает, что данная функция не содержит в своем составе компонент, имеющих форму второй, ортогональной ей функции.
Если совокупность функций Сk(t) удовлетворяет также и условию
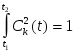 ,
,то она называется ортонормированной.
Если два вышеприведенных условия ортонормированности функций Сk(t) выполняются, то получаем
 .
.Если второе условие не выполнено и совокупность функций является только ортогональной, но не ортонормированной, то
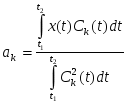 . (2)
. (2)Следовательно, сложный детерминированный сигнал х(t) на интервале (t2-t1) можно заменить суммой т взаимно ортогональных на этом интервале сигналов Сk(t). Погрешность такой аппроксимации будут зависеть от числа членов ряда m и сходимости ряда.
В качестве ортогональных функций используются либо элементарные функции, например тригонометрические, либо специальные функции.
Наиболее часто в качестве ортогональных функций используются тригонометрические функции, образующие обычный ряд Фурье. Ортогональными на любом интервале
при t0<t<t0+Т.
Коэффициенты aiряда Фурье определяются по формулам:
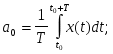


Тригонометрический ряд Фурье применяют также в следующей форме:
где
Аналогично можно показать, что комплексные экспоненциальные функции

Если k=п, то I=Т, а при кп I=0.
Следовательно, любой периодический сигнал х(t) можно представить суммой комплексных экспоненциальных сигналов с помощью экспоненциального ряда Фурье
Коэффициенты экспоненциального ряда Фурье определяются по формуле

Экспоненциальный ряд Фурье для периодической функции является второй формой тригонометрического ряда Фурье.
Периодический сигнал с периодом повторения T можно представить состоящим из периодических синусоидальных сигналов с частотными составляющими =2/Т; 2; З; ...; n. Периодический сигнал х(t) обладает дискретным или линейчатым спектром, графически изображающимся в виде вертикальных линий вдоль оси частот в точках , 2 и т.д. причем высота каждой из этих линий пропорциональна амплитуде данной частотной составляющей (гармоники).
Обычно частотные составляющие спектра являются комплексными числами, и поэтому для представления данной периодической функции необходимо иметь два дискретных спектра: спектр амплитуд и спектр фаз (рис. 1). Однако во многих случаях частотные составляющие являются только действительными или только мнимыми, и тогда сигнал можно представить одним спектром, так как его фазовый спектр постоянен и имеет составляющие, соответственно равные 0 или 90°.
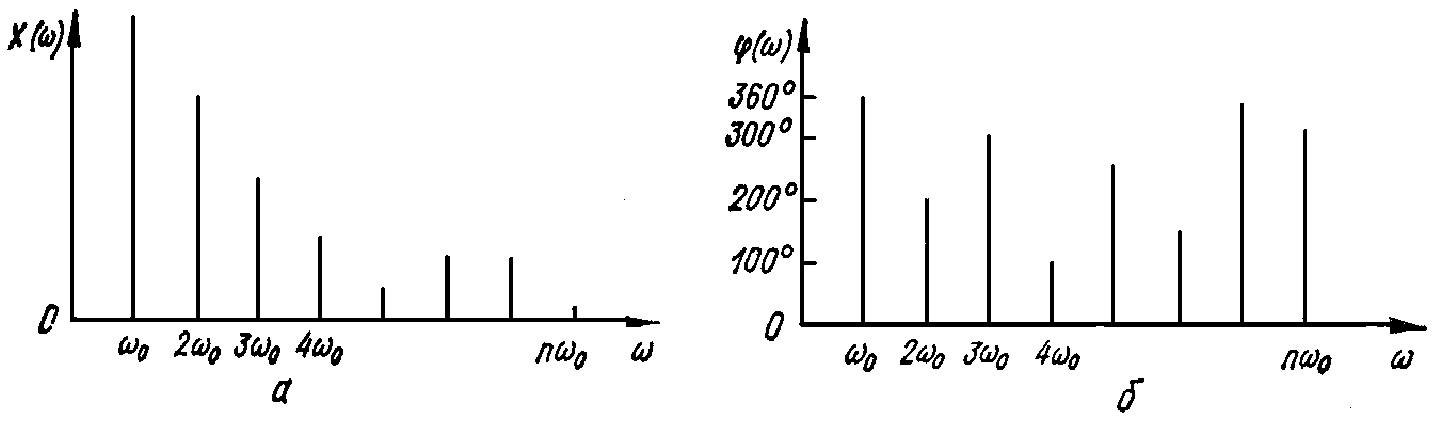
Рис. 1 Спектр амплитуд (а) и спектр фаз (б) периодического сигнала
Дискретный спектр периодического сигнала, определяемый с помощью средств измерений, называемых анализаторами гармоник, характеризуется совокупностью важных информативных параметров сигнала х(t) значениями амплитуд и фаз отдельных гармоник, полосой частот и др.
Под нелинейными искажениями (НИ) понимается любое изменение сигнала, вызывающее искажения передаваемого сообщения и обусловленное нелинейностью тракта. Количественная оценка НИ может быть произведена различными методами: гармоническими, комбинационными, статистическими. Наибольшее применение получили измерители нелинейных искажений, предназначенные для измерения степени искажения формы кривой, т. е. отличия формы сигнала от гармонической. Количественно искажения оценивают двумя коэффициентами: коэффициентом гармоник KГ и коэффициентом нелинейных искаженийKНИ.
На практике коэффициент гармоник рассчитывается по формуле
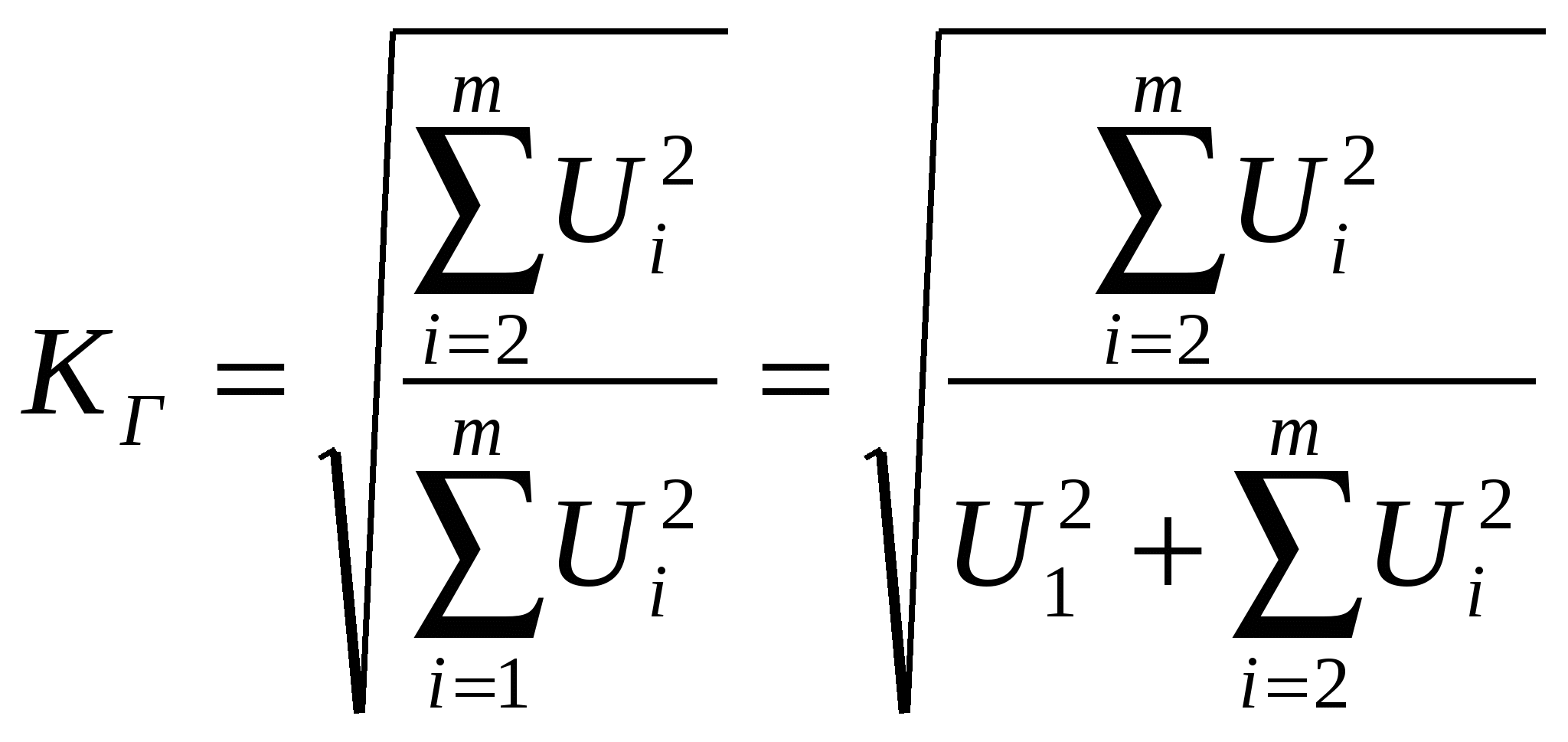 ,
,где Ui – амплитуда i-й гармоники выходного сигнала.
Из этой формулы видно, что значение коэффициента КГ может изменяться в пределах от 0 до 1.
Коэффициент нелинейных искажений рассчитывается по формуле
 ,
,где U1 – амплитуда первой гармоники.
Как правило, измерители нелинейных искажений определяют коэффициент гармоник, а коэффициент нелинейных искажений рассчитывают по простой формуле
Видно, что значение коэффициента КНИ может изменяться от 0 до ∞.
При малых КНИможно считать, что КНИ≈КГ (в диапазоне КНИ≤0,1 значения КГ и КНИ отличаются менее чем на 1%.
3. Практическая часть
Программа Workbench позволяет проводить спектральный анализ сигналов различной формы. В ходе лабораторной работы мы проведем спектральный анализ простейших периодических сигналов, наиболее часто встречающихся в электронной технике. Это сигналы синусоидальной, прямоугольной и треугольной формы.
Периодический сигнал с прямоугольными импульсами широко используется ввиду простоты генерирования несложными логическими интегральными элементами и описывается следующей функцией:
Параметрами периодического сигнала с прямоугольными импульсами являются: амплитуда Xm, период T0 и длительность импульса . Любой из этих параметров может быть информативным. Кроме того, определяется еще один параметр – скважность (рис. 6.8):
Q=Tц/,
или обратный ему параметр, называемый коэффициентом заполнения (duty cycle):
q=/Tц.
Для проведения спектрального анализа этих сигналов необходимо:
3.1 Собрать схему, приведенную на рис. 2 справа.

Рис. 2
Дважды щелкнуть по изображению функционального генератора. Откроется окно, показанное на рис. 2 слева. На генераторе будут установлены параметры предыдущего включения. Для выполнения задания нужно установить свои параметры.
Щелкнуть в окне функционального генератора на кнопку с изображением синусоиды.
В поле Frequency установить значение n кГц, где n – порядковый номер студента в списке группы, в поле Dutycycle установить значение 50, в поле Amplitude значение 10 В, в поле Offset значение 0.
Двойным щелчком по осциллографу раскрыть его. Настроить начальную развертку осциллографа. В поле Timebase установить начальное значение 0,5 мкс/дел. В поле ChannelA установить значение развертки по вертикали 5 В/дел.
В пункте меню Analysis/AnalysisOptions... в закладке Instruments поставить птичку перед надписью Pauseaftereachscreen и нажать кнопку ОК. Это означает, что после каждого заполнения экрана осциллографа моделирование будет приостанавливаться, чтобы была возможность наблюдать сигнал.
Запустить моделирование из пункта меню Analysis/Activate или, нажав на изображение выключателя в верхнем правом окне программы.
Подбирая развертку, убедиться, что на экране осциллографа наблюдается сигнал требуемой формы (тот, кнопка которого нажата в окне функционального генератора).
Остановить моделирование, выбрав пункт меню Analysis/Stop или нажав на изображение выключателя в верхнем правом окне программы.
Все подготовлено для проведения спектрального анализа.
Провести спектральный анализ. Для этого нужно выбрать пункт меню Analysis/Fourier... Появится диалоговое окно, в котором в поле FundamentalFrequency установить значение частоты n кГц, а в поле Numberofharmonics значение 50. Нажать кнопку Simulate и получить изображение спектра исследуемого сигнала.
Изображение сигнала (с экрана осциллографа) и его спектра следует скопировать и вставить в таблицу 1. Записать в таблицу соответствующее значение Totalharmonicdistortion (коэффициента гармоник). Закрыть окно результатов моделирования.
В окне функционального генератора нажать на кнопку с изображением сигнала треугольной формы. В поле Dutycycle установить значение n. Понаблюдать форму сигнала на осциллографе, выполнив пункты 3.7 3.9
Провести спектральный анализ сигнала треугольной формы, выполнив пункты 3.10 3.11. Изображение сигнала и его спектра следует скопировать и вставить в таблицу 1.
Повторить спектральный анализ сигнала треугольной формы для значений Dutycycle равных 50 и (100-n).
В окне функционального генератора нажать на кнопку с изображением сигнала прямоугольной формы. В поле Dutycycle установить значение n. Понаблюдать форму сигнала на осциллографе, выполнив пункты 3.7 3.9
Провести спектральный анализ, выполнив пункты 3.10 3.11. Изображение сигнала и его спектра следует скопировать и вставить в таблицу 1.
Повторить спектральный анализ сигнала прямоугольной формы для значений Dutycycle равных 50 и (100-n).
Таблица 1
| № п/п | Изображение сигнала | Значение Duty cycle | Изображение спектра сигнала | Коэффициент гармоник |
| 1 | | 50 | | |
| 2 | | n | | |
| 3 | | 50 | | |
| 4 | | 100-n | | |
| 5 | | n | | |
| 6 | | 50 | | |
| 7 | | 100-n | | |
Контрольные вопросы по заданию
Что такое «спектр сигнала»?
Что означает «разложить сигнал в ряд Фурье» и какие сигналы можно разлагать в ряд Фурье?
Какие функции называются элементарными?
Смысл параметра «коэффициент гармоник»?
Смысл параметра «Dutycycle»?
БЕЛОРУССКИЙ НАЦИОНАЛЬНЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Контрольная работа по дисциплине
“Преобразование измерительной информации”
Выполнил: студент группы 31301213 ПСФ
Иванов И.И.
Проверил: Невдах В.В.
Минск
2015
1 Для удобства работы в пункте меню Circuit / Schematic Options... на вкладке Show/Hide напротив надписей Show reference ID и Show nodes поставьте галочки.
2 Для удобства работы в пункте меню Circuit / Schematic Options... на вкладке Show/Hide напротив надписей Show reference ID и Show nodes поставьте галочки.
3 Для удобства работы в пункте меню Circuit / Schematic Options... на вкладке Show/Hide напротив надписей Show reference ID и Show nodes поставьте галочки.
4 Для удобства работы в пункте меню Circuit / Schematic Options... на вкладке Show/Hide напртив надписей Show reference ID и Show nodes поставьте галочки.












