роторный вибрационный гироскоп. Курсовая работа по ИДСУ. Отчет по курсовой работе Название Роторный вибрационный гироскоп. Условия резонансной настройки роторного вибрационного гироскопа
 Скачать 0.87 Mb. Скачать 0.87 Mb.
|
Институт № 3 «Системы управления, информатика и электроэнергетика» Кафедра №305 «Автоматизированные комплексы систем ориентации и навигации» Направление подготовки «24.05.06 Системы управления летательными аппаратами» Отчет по курсовой работе Название: «Роторный вибрационный гироскоп. Условия резонансной настройки роторного вибрационного гироскопа» Дисциплина: Инерциальные датчики систем управления
Москва, 2021 Оглавление Введение Функциональная схема двухстепенного РВГ Уравнение движения РВГ по углу α Условие резонансной настройки Список использованной литературы Введение Роторный вибрационный гироскоп (РВГ) относится к классу динамически настраиваемых гироскопов. Роторный вибрационный гироскоп используется для измерения углов поворота, угловых скоростей в системе ориентации и навигации. Также он является гироскопическим чувствительным элементом. Точность - 1⁰/час – достаточно грубый, из-за чего не пригоден в авиации, но найти свое применение может на торпедах. В данной работе будет рассмотрена функциональная схема РВГ, принцип работы и условие резонансной настройки. Функциональная схема двухстепенного РВГ Функциональная схема двухстепенного РВГ приведена на рисунке 1 ниже: 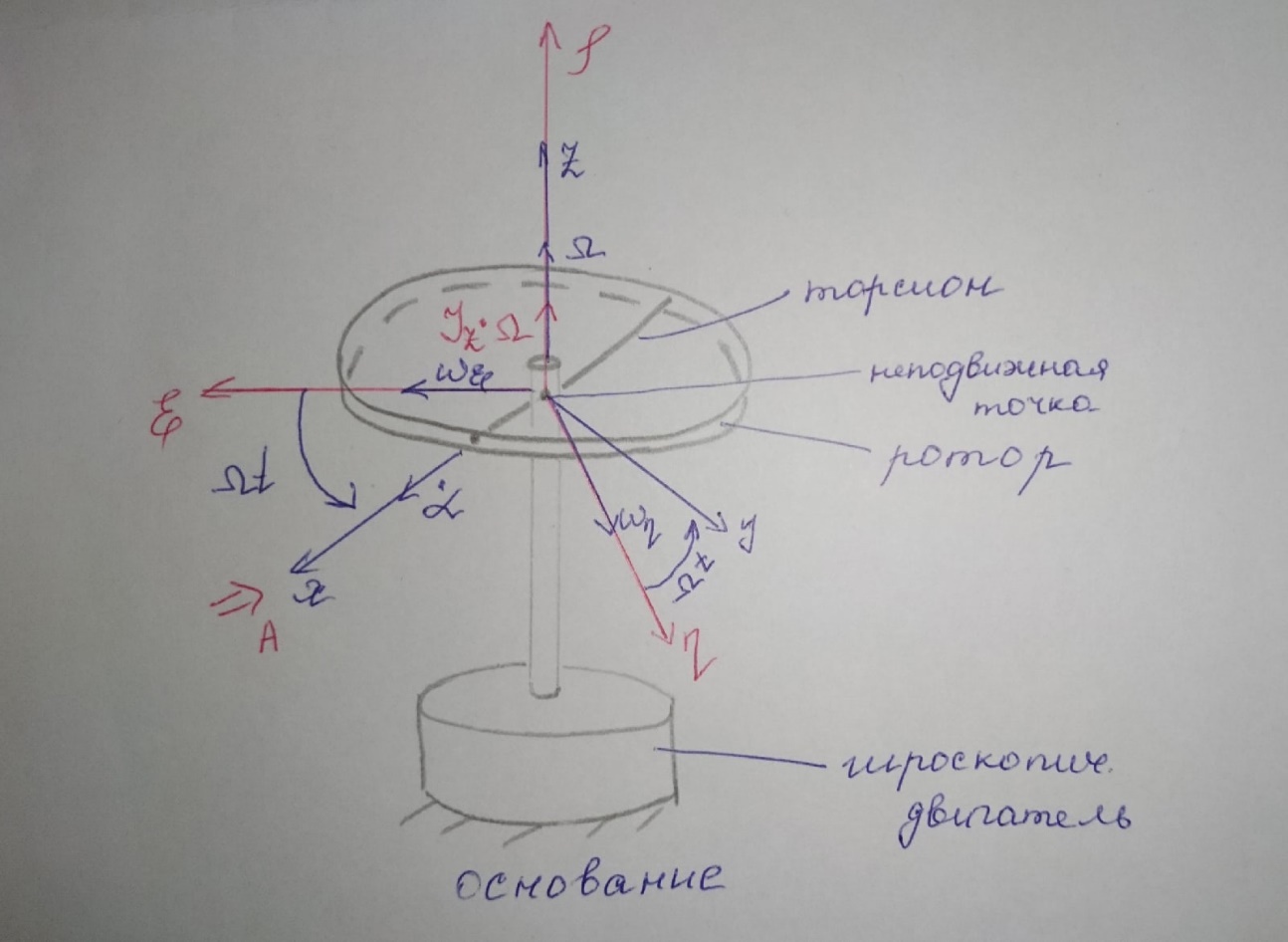 Рисунок 1 – Функциональная схема двухстепенного РВГ Пояснения к обозначениям на схеме: t – время, ω – угловая скорость вращения, представляющая собой постоянную величину, ξηζ – система координат, жестко связанная с основанием, xyz – система координат, жестко связанная с ротором, Iz*ω – кинетический момент ротора за счет вращения ротора ωξ, ωη – проекции угловой скорости вращающегося основания на ξ и η, которые измеряет гироскоп. На основании установлен двигатель. Этот двигатель вращает вал с большой угловой скоростью Ω (до 10000-15000 об/мин.), с валом через торсионы связан ротор (торсионы – подобие струн, которые не растягиваются). Торсионы могут закручиваться с ротором относительно вала вокруг оси х на угол α. Торсионы имеют бесконечную жесткость. При вращении двигателя вместе с валом вокруг оси z через торсионы увлекается ротор и вращается вместе с валом. Таким образом, ротор имеет две степени свободы относительно основания: угол поворота вместе с валом вокруг оси ζ, угол поворота вокруг вращающейся оси х. Можно показать, что при вращениях основания ωξ, ωη возникают гироскопические моменты, в частности вокруг оси х, под действием которых ротор/маховик поворачивается по углу α и угол α несет информацию об угловых скоростях ωξ, ωη. Уравнение движения РВГ по углу α Воспользовавшись принципом Даламбера, можно спроектировать все моменты, приложенные на ось х торсионов. Сумма всех моментов равняется нулю. Вид А: 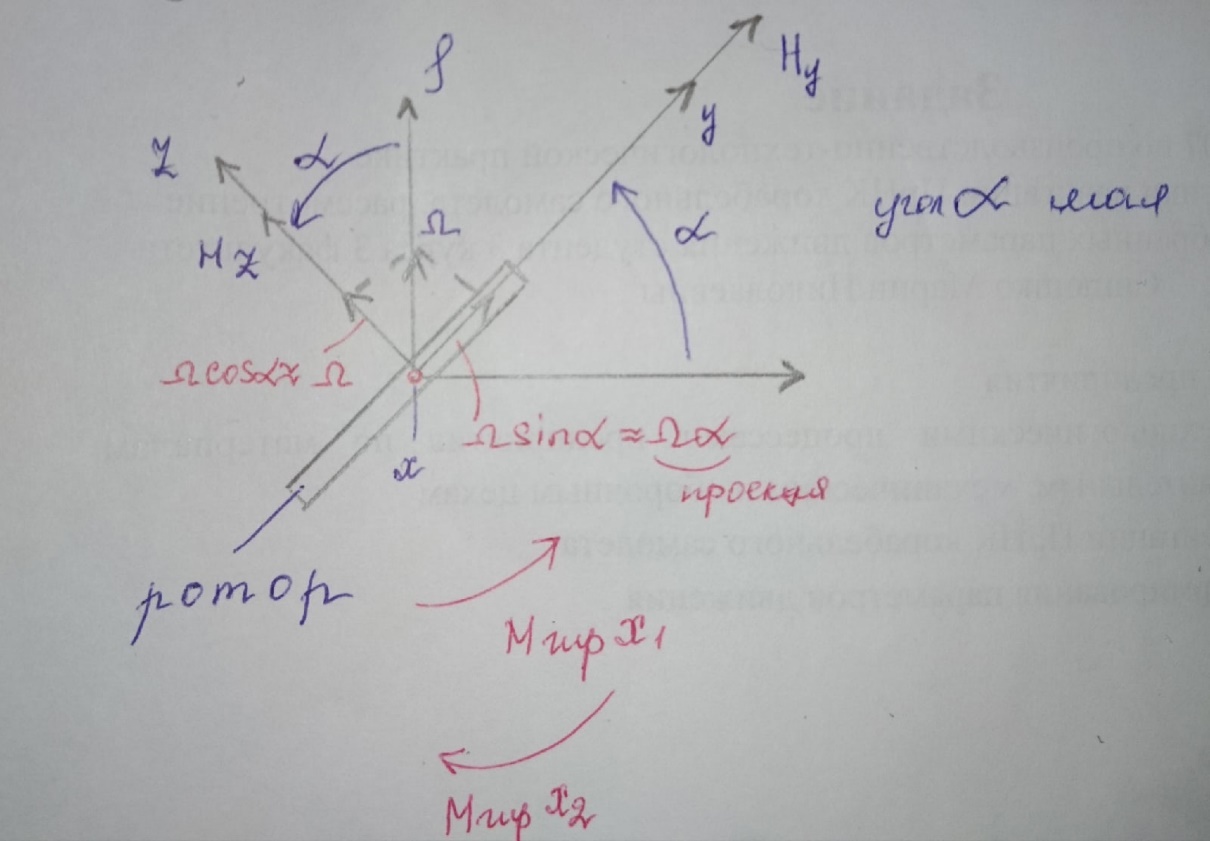 Рисунок 2 – Вид А Hy=Iy*Ωα(1) За счет Ωα(проекции угловой скорости) по оси y направлен кинетический момент Hy. Hz=Iz*Ω (2) Hy и ω порождают гироскопический момент МГИРХ1: МГИРХ1=Hy* Ω=Iy*Ω2α(3) Hz и Ωα порождают гироскопический момент МГИРХ2: МГИРХ2=-Hz* Ωα=-Iz*Ω2α(4) МГИРХ=-(Iz-Iy)*Ω2α(5) Момент МГИРХаналогичен моменту упругости. 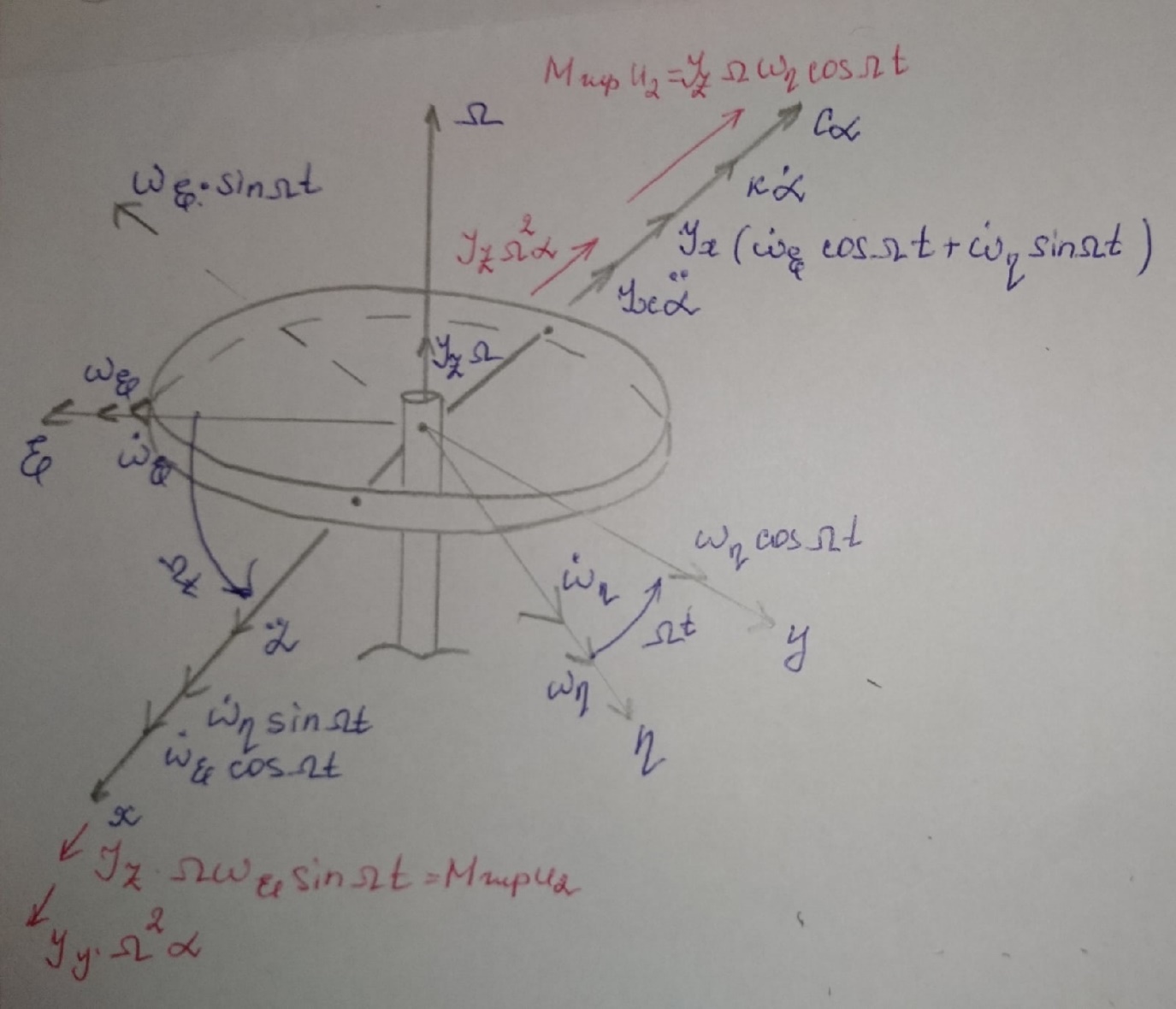 Рисунок 3 -Iх( 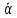 + +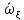 *cosΩt+ *cosΩt+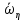 sinΩt)-k sinΩt)-k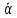 -cα-Iz*Ω2α+Iy*Ω2α- Iz*Ωωη*cosΩt+Iz*Ωωξ*sinΩt=0 (6) -cα-Iz*Ω2α+Iy*Ω2α- Iz*Ωωη*cosΩt+Iz*Ωωξ*sinΩt=0 (6)Выражение выше можно переписать в виде: T2 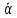 +2ξT +2ξT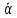 +α=bωξsinΩt-bωηcosΩt-T2 +α=bωξsinΩt-bωηcosΩt-T2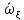 cosΩt-T2 cosΩt-T2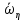 sinΩt, (7) sinΩt, (7)где bωξsinΩt-bωηcosΩt– информационное воздействие, T – постоянная времени. В (7) информационное воздействие по α порождают первые два гироскопических момента. T2= 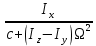 ; (8) ; (8)Ix=Iy; (9) ξ= 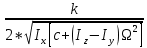 (10) (10)Отбрасывая 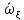 и и 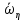 получается следующее: получается следующее:T2 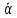 +2ξT +2ξT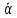 +α=bωξsinΩt-bωηcosΩt. (11) +α=bωξsinΩt-bωηcosΩt. (11)Вынужденная составляющая решения (11): α= αвын=А(Ω) 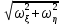 sin(Ωt-ψ(Ω)), (12) sin(Ωt-ψ(Ω)), (12)где А(Ω) – величина АЧХ при текущей частоте, равной частоте вращения, ψ(Ω) – фазовый сдвиг по отношению к входной гармонике синуса. ψ(Ω)=arctg 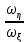 +arctg +arctg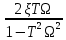 , (13) , (13)А(Ω)= 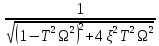 ,. (14) ,. (14)Таким образом, гироскопические моменты за счет ωξи ωη порождают гармонические колебания ротора на частоте вращения с амплитудой, зависящей от компонент угловой скорости вращения основания. С целью увеличения чувствительности гироскопа по отношению к измеряемым ωξи ωη целесообразно увеличивать А(Ω). Для этого стремятся уменьшить ξ (степень затухания) и обеспечит условие соблюдения резонансной настройки. Условие резонансной настройки 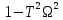 =0 (15) =0 (15)Угловая скорость вращения вала из выражения (15): Ω= 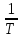 , (16) , (16)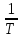 – частота собственных недемпфированных колебаний. – частота собственных недемпфированных колебаний. Частота воздействия гироскопических моментов равна частоте собственных колебаний ротора или маховика относительно оси торсионов. Отсюда на основе (8): 1- 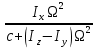 =0; (17) =0; (17)Ω= 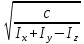 . (18) . (18)Если маховик симметричен ( 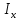 = =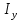 ): ):Ω= 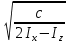 . (19) . (19)Подставим условие резонансной настройки (15) в выражение (12) получим (20): α= 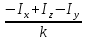 (ωξcosΩt+ωηsinΩt). (20) (ωξcosΩt+ωηsinΩt). (20)Угол α измеряется датчиком угла. Сигнал по α поступает на схему синхронного детектирования. 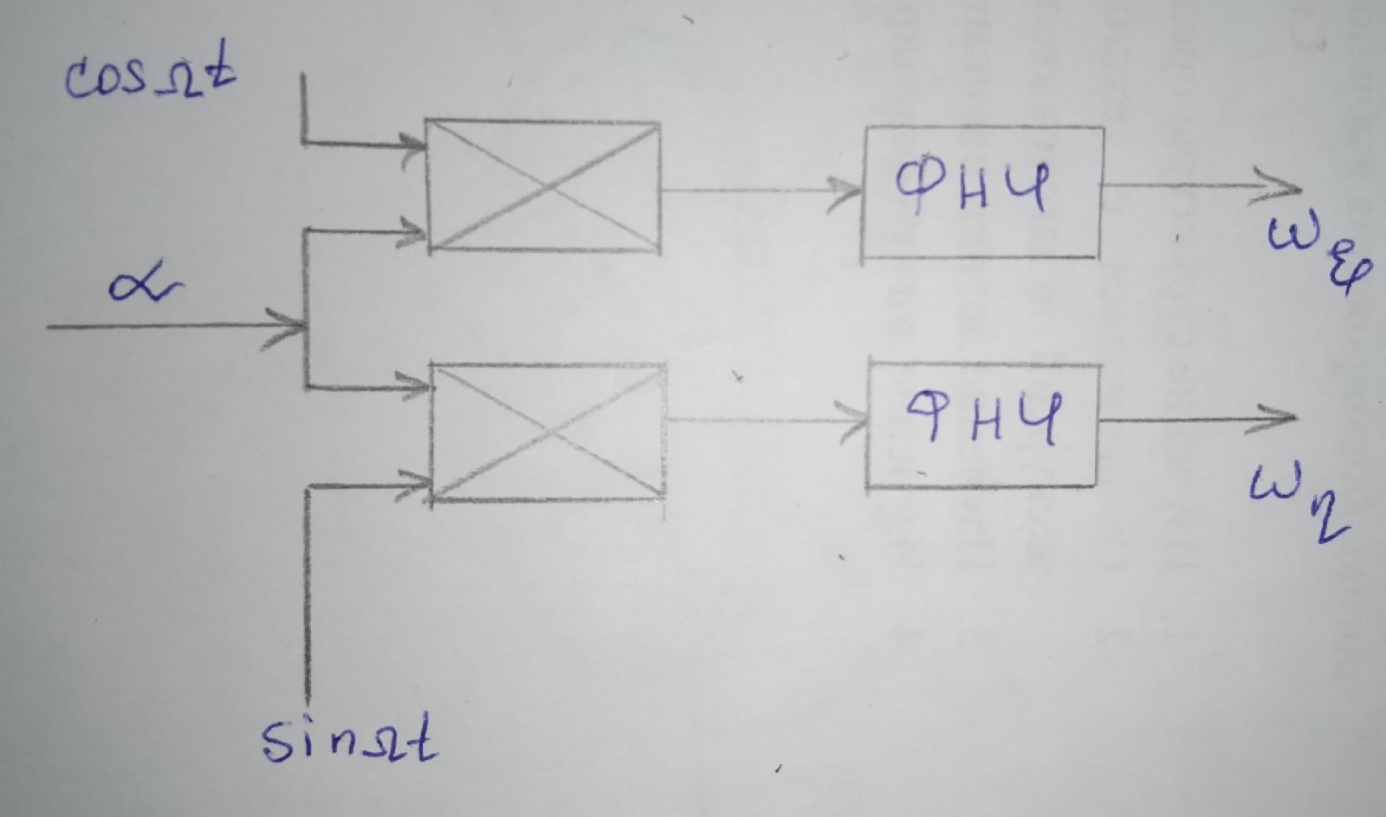 Рисунок 4 – Схема синхронного детектирования На схеме выше ФНЧ – фильтр низких частот (не пропускает высокие частоты). α*cosΩt=- 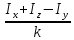 (ωξcos2Ωt+ωηcosΩt*sinΩt)= - (ωξcos2Ωt+ωηcosΩt*sinΩt)= -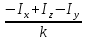 (ωξ (ωξ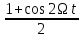 +ωη* +ωη*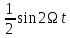 ); (21) ); (21)<α*cosΩt>=- 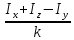 * *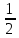 ωξ. (22) ωξ. (22)Аналогично: <α*sinΩt>=- 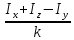 * *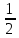 ωη. (23) ωη. (23)Согласно (22) и (23) любой гироскоп является двухкомпанентным измерителем. (22) и (23) справедливы, если имеют место быстрые затухания свободных составляющих уравнения (11). Информацию о вращениях основания можно получить также измеряя углы поворота маховика/ротора не относительно оси торсионов, а относительно осей, связанных с основанием (ξ и η). 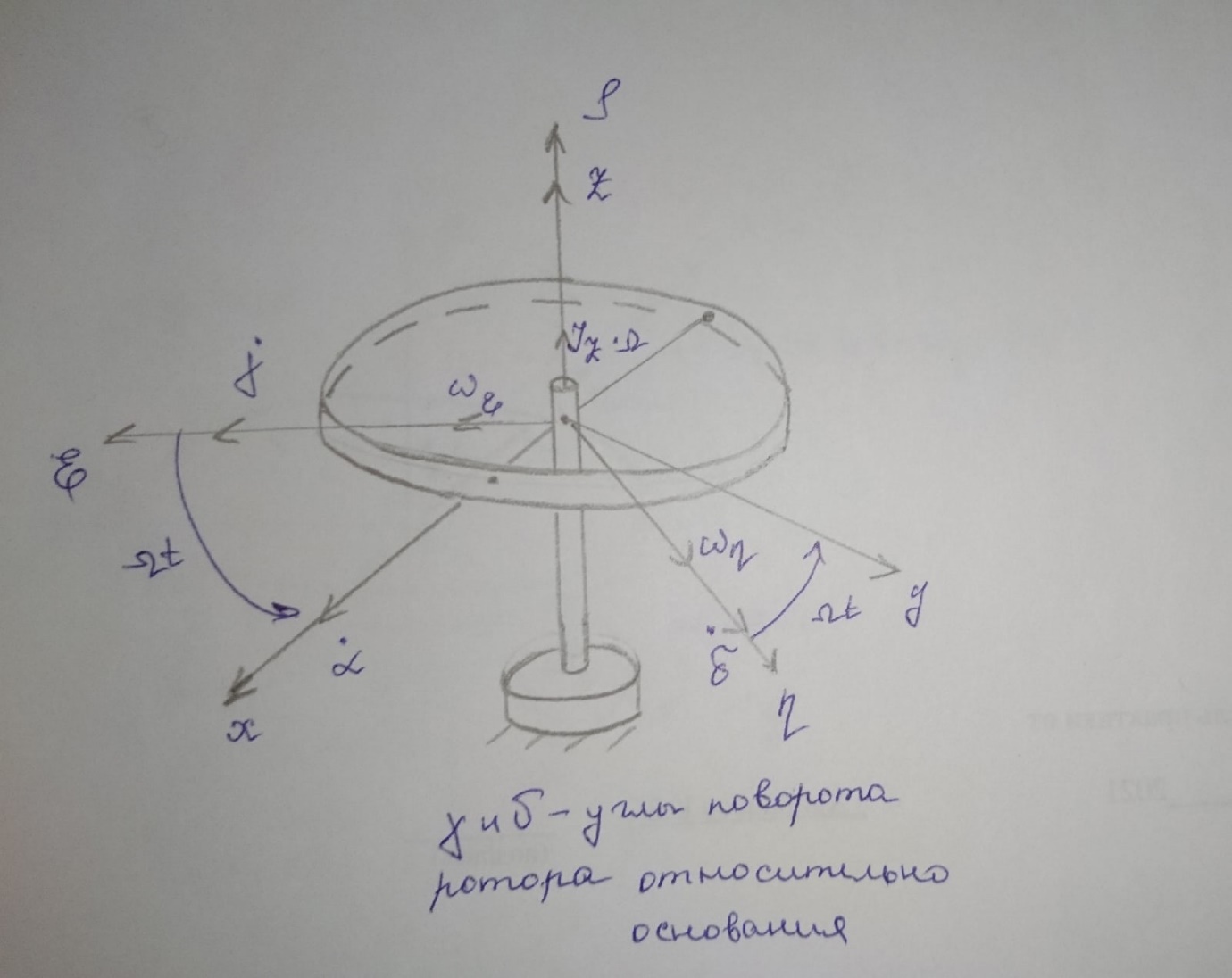 Рисунок 5 На рисунке γ и δ – углы поворота ротора относительно основания. Выполняется: γ=αcosΩt, δ=αsinΩt(24) Введем комплексный угол (25): θ=γ+jδ, (25) Тогда связь между α и θ: α= θ*e-jΩt, (26) гдеe-jΩt – оператор вращения. Подставляя (26) в (11) получим комплексное уравнение и приравняем раздельно в этом уравнении мнимы е и действительные части: T2 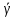 +2T2Ω +2T2Ω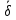 +2ξT +2ξT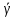 +(1-T2 +(1-T2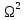 )γ+2ξTΩδ= )γ+2ξTΩδ=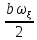 * *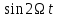 - -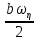 (1+ (1+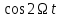 ), (27) ), (27)где первое слагаемое – традиционный член, порождающий нутационные колебания, второе слагаемое – гироскопический момент, третье – демпфирующий момент, четвертое – момент типа позиционного (в скобках угловая скорость пружины), пятое – элемент демпфирования, шестое, седьмое, восьмое – гироскопические моменты. С помощью датчиков углов можно измерять углы α и δ, отфильтровывать компоненты, идущие на второй частоте. В выходном сигнале сохраняются квазипостоянные компоненты. Будем полагать, что выполняется условие резонансной настройки (15). Выполнение (15) в (27) означает устранение позиционной связи ротора с основанием, в то время как (15) выполняясь в (11) означает наличие явления резонанса. Если выполняются все принятые допущения, получаем (29) и (30): 2T2Ω 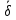 =- =-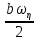 , δ= , δ=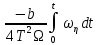 (29) (29)2T2Ω 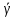 =- =-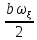 , γ= , γ=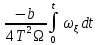 (30) (30)Cогласно (29) и (30) в этом случае РВГ является двухкомпонентным интегрирующим гироскопом (углы поворота основания вокруг осей ξ и η). Список использованной литературы Лекции по курсу «гироскопические приборы» Черноморского А.И. Прикладная теория гироскопов/Лукьянов А.П.,Раскопов В.Я., Филатов Ю.В. Роторный вибрационный гироскоп РВГ — КиберПедия. URL –https://cyberpedia.su/15x25f3.html |

