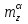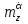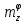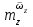испытание комплексной системы управления курсовая. Курсовая работа Матковский ИКСУЛА. Отчет по курсовой работе специальность 24. 05. 03 Испытание летательных аппаратов Квалификация (степень) студента Инженер
 Скачать 4.33 Mb. Скачать 4.33 Mb.
|
|
Министерство науки и высшего образования Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования «Московский авиационный институт (национальный исследовательский университет)» (МАИ) Филиал «Взлет» в г. Ахтубинске ОТЧЕТ ПО КУРСОВОЙ РАБОТЕ Специальность: 24.05.03 Испытание летательных аппаратов Квалификация (степень) студента: Инженер Специализация: Летные испытания пилотируемых авиационных и воздушно-космических летательных аппаратов Форма обучения: очная
Ахтубинск 2020 1. Задача о системе автоматического управления креном. 1.1. Задача. Система автоматического управления креном самолета (САУ креном) предназначена для автоматической стабилизации заданного значения крена 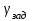 или приведения самолета из исходного положения по крену к заданному. В первом случае говорят о решении задачи стабилизации, а во втором - о решении задачи управления. или приведения самолета из исходного положения по крену к заданному. В первом случае говорят о решении задачи стабилизации, а во втором - о решении задачи управления.Рассмотрим решение задач стабилизации и управления применительно к изолированному движению самолета, органами поперечного управления которого служат элероны, в канале крена. Система уравнений, описывающих движение самолета с САУ креном содержит два дифференциальных уравнения, описывающих изменение скорости крена 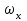 и собственно крена и собственно крена 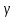 и алгебраическое уравнение, определяющее характер отклонения элеронов и алгебраическое уравнение, определяющее характер отклонения элеронов 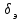 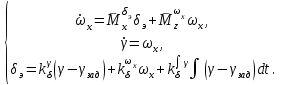 Третье уравнение системы с точки зрения теории управления представляет собой PID-регулятор (P - пропорциональный, I - интегральный, D - дифференциальный). Пропорциональный член регулятора 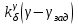 обеспечивает формирование сигнала для отклонения элеронов с целью устранения рассогласования между текущим обеспечивает формирование сигнала для отклонения элеронов с целью устранения рассогласования между текущим 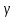 и заданным и заданным 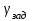 значениями крена. значениями крена. 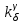 - безразмерный коэффициент пропорциональности, определяющий величину потребного отклонения элеронов в градусах (радианах) при наличии рассогласования по крену в 1 градус (радиан). Пропорциональный член обеспечивает отклонение элеронов пропорционально рассогласованию по крену. - безразмерный коэффициент пропорциональности, определяющий величину потребного отклонения элеронов в градусах (радианах) при наличии рассогласования по крену в 1 градус (радиан). Пропорциональный член обеспечивает отклонение элеронов пропорционально рассогласованию по крену.В подавляющем большинстве случаев собственное аэродинамическое демпфирование самолетов в канале крена недостаточно. Поэтому в закон работы САУ креном включается дифференциальный член 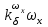 , улучшающий качество переходного процесса. Дифференциальным этот член называется потому, что отклонение элеронов осуществляется пропорционально производной крена , улучшающий качество переходного процесса. Дифференциальным этот член называется потому, что отклонение элеронов осуществляется пропорционально производной крена 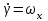 . Коэффициент пропорциональности . Коэффициент пропорциональности 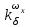 измеряется в с-1 и определяет потребную величину отклонения элеронов в градусах или радианах для компенсации скорости крена в 1 градус или радиан в секунду. Дифференциальный член обеспечивает отклонение элеронов для компенсации производной крена - скорости крена и, таким образом, является по своей сути демпфирующим. измеряется в с-1 и определяет потребную величину отклонения элеронов в градусах или радианах для компенсации скорости крена в 1 градус или радиан в секунду. Дифференциальный член обеспечивает отклонение элеронов для компенсации производной крена - скорости крена и, таким образом, является по своей сути демпфирующим.Интегральный член закона управления САУ креном 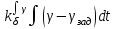 обеспечивает астатизм управления. В том случае, если используется PD - регулятор (без интегрального члена), то безошибочное автоматическое управление обеспечивается только при отсутствии постоянно действующих внешних возмущений. Так как на практике такие возмущения всегда имеют место (атмосферная турбулентность, несимметричные внешние подвески и деформации конструкции), то САУ креном решает задачи стабилизации и управления со статической ошибкой. Введение интегрального члена в закон управления устраняет эту ошибку, а регулятор с интегральным членом называют астатическим. обеспечивает астатизм управления. В том случае, если используется PD - регулятор (без интегрального члена), то безошибочное автоматическое управление обеспечивается только при отсутствии постоянно действующих внешних возмущений. Так как на практике такие возмущения всегда имеют место (атмосферная турбулентность, несимметричные внешние подвески и деформации конструкции), то САУ креном решает задачи стабилизации и управления со статической ошибкой. Введение интегрального члена в закон управления устраняет эту ошибку, а регулятор с интегральным членом называют астатическим.1.2. Выполнение работы в MatlabSimulink. Рассмотрим Simulink - модель динамики самолета в изолированном движении крена, записанную в форме Коши. Пусть закон работы САУ креном является статическим, то есть не содержит интегрального члена. В таком случае Simulink - модель динамики самолета со статической САУ креном при  и и  может быть сформирована так, как показано на рисунке 1. может быть сформирована так, как показано на рисунке 1.На рисунке 2 представлены результаты моделирования в предположении, что на 2-й секунде в САУ приходит сигнал 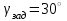 . . Рисунок 1- Simulink - модель динамики самолета в изолированном движении крена под управлением статической САУ креном.  Рисунок 2- Результаты моделирования движения самолета со статической САУ креном. Исходный режим - полет без крена. Выход самолета на заданный крен осуществляется примерно на 7-й секунде моделирования после незначительного перерегулирования. Подбором коэффициентов усиления САУ обеспечивается коррекция переходного процесса. Рассмотрим поведение самолета со статической САУ креном при наличии возмущения по крену, вызванного, например, образованием несимметричной внешней подвески под левой консолью крыла. В таком случае дифференциальное уравнение для скорости крена следует представить в следующем виде 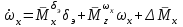 , где , где 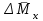 - приведенный относительно осевого момента инерции момент от внешней подвески, вызванный ее весом на плече до плоскости симметрии самолета. Пусть - приведенный относительно осевого момента инерции момент от внешней подвески, вызванный ее весом на плече до плоскости симметрии самолета. Пусть 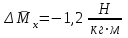 . Кроме того, пусть образование несимметричной конфигурации происходит на 10-й секунде моделирования в то время, когда САУ креном уже вывела самолет на заданный крен . Кроме того, пусть образование несимметричной конфигурации происходит на 10-й секунде моделирования в то время, когда САУ креном уже вывела самолет на заданный крен 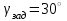 . При таких условиях Simulink - модель дифференциального уравнения для скорости крена может быть представлена так, как показано на рисунке 3. . При таких условиях Simulink - модель дифференциального уравнения для скорости крена может быть представлена так, как показано на рисунке 3.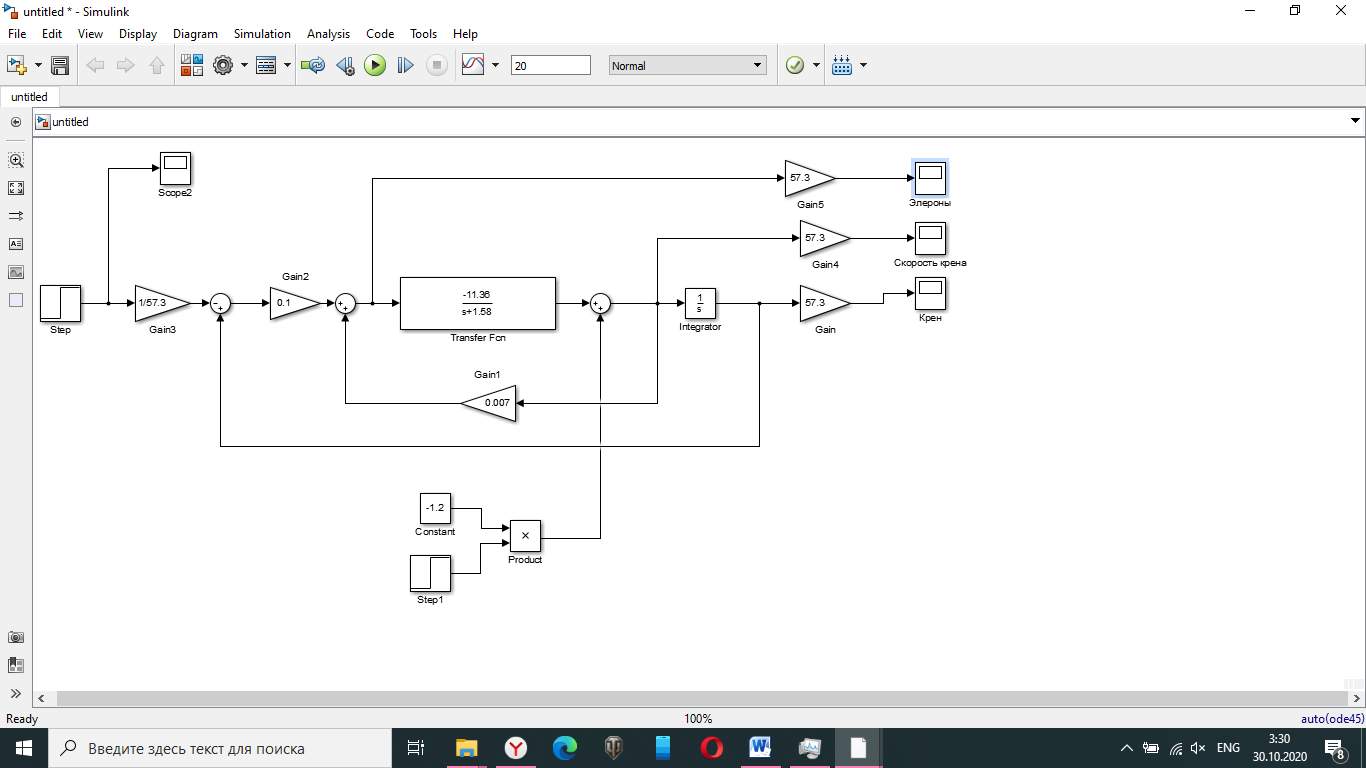 Рисунок 3- Simulink - модель дифференциального уравнения для скорости крена с дополнительным моментом от несимметричной подвески.  Рисунок 4- Результаты моделирования движения самолета с несимметричной подвеской и статической САУ креном. На рисунке 4 представлены результаты моделирования динамики самолета с несимметричной внешней подвеской и статическим САУ креном. Видно, что на 10-й секунде моделирования происходит отклонение элеронов для компенсации мгновенно развившегося возмущающего момента. При этом примерно на 16-й секунде самолет балансируется с креном около 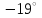 в то время, когда в то время, когда 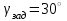 . Это и есть статическая ошибка. . Это и есть статическая ошибка.Рассмотрим Simulink - модель астатической САУ креном (рисунок 5), закон управления которой соответствует PID - регулятору с коэффициентом усиления при интегральном члене 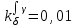 . Результат функционирование такой САУ при условиях прежней задачи свидетельствует о том, что на 16-й секунде моделирования ошибка между текущим и заданным значениями крена существенно меньше, чем в предыдущем случае и, кроме того, она монотонно стремиться к дальнейшему уменьшению (рисунок 6). Полностью ошибка устраняется примерно на 50-й секунде моделирования. . Результат функционирование такой САУ при условиях прежней задачи свидетельствует о том, что на 16-й секунде моделирования ошибка между текущим и заданным значениями крена существенно меньше, чем в предыдущем случае и, кроме того, она монотонно стремиться к дальнейшему уменьшению (рисунок 6). Полностью ошибка устраняется примерно на 50-й секунде моделирования.Таким образом, введение интегрального члена в закон функционирования САУ позволяет устранить ошибки при постоянно действующих возмущениях, однако переходный процесс затягивается по времени.  Рисунок 5- Simulink - модель астатической САУ креном. 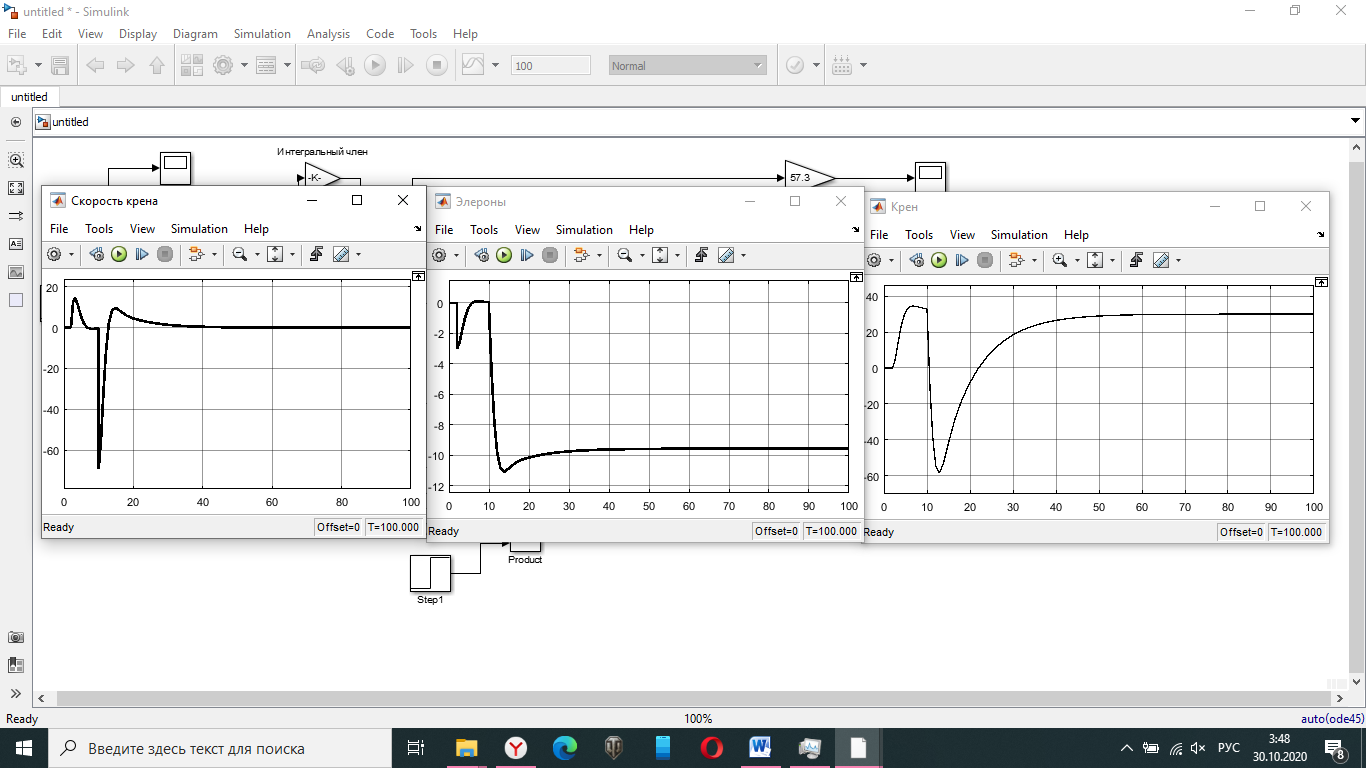 Рисунок 6- Результат моделирования астатической САУ креном. 2. Система автоматического управления курсом. 2.1. Задача. Управления и стабилизации курса выполняется в интересах решения навигационных задач. Курсом называется угол 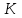 между продольной осью самолета и направлением на север (истинный курс) или направлением магнитного меридиана (магнитный курс). При полете по маршруту курс отсчитывается от направления на поворотные пункты этого маршрута. Численно курс отсчитывается по часовой стрелке от базового направления (направления на север или магнитный меридиан), всегда положительный и измеряется от 0 до между продольной осью самолета и направлением на север (истинный курс) или направлением магнитного меридиана (магнитный курс). При полете по маршруту курс отсчитывается от направления на поворотные пункты этого маршрута. Численно курс отсчитывается по часовой стрелке от базового направления (направления на север или магнитный меридиан), всегда положительный и измеряется от 0 до 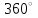 . .В динамике полета для описания движения летательных аппаратов в горизонтальной плоскости принято оперировать углом поворота траектории (углом пути) 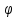 и углом рыскания и углом рыскания 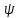 . Связь между этими углами устанавливается углом скольжения . Связь между этими углами устанавливается углом скольжения 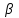 в виде в виде  . Углы . Углы 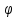 и и 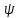 отсчитываются от базового направления и измеряются от 0 до отсчитываются от базового направления и измеряются от 0 до 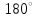 при отсчете против часовой стрелки и от 0 до при отсчете против часовой стрелки и от 0 до 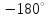 при отсчете по часовой стрелке. Искривление траектории в горизонтальное плоскости может осуществляться двумя способами: без крена путем создания скольжения (разворот «блинчиком») и за счет создания крена при скольжении, близком к нулю. Второй вариант с точки зрения минимизации времени выполнения маневров более предпочтителен и будет рассматриваться далее. При этом будем полагать, что скольжение отсутствует, а, следовательно при отсчете по часовой стрелке. Искривление траектории в горизонтальное плоскости может осуществляться двумя способами: без крена путем создания скольжения (разворот «блинчиком») и за счет создания крена при скольжении, близком к нулю. Второй вариант с точки зрения минимизации времени выполнения маневров более предпочтителен и будет рассматриваться далее. При этом будем полагать, что скольжение отсутствует, а, следовательно  . Графическая интерпретация углов курса . Графическая интерпретация углов курса 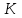 и рыскания и рыскания 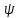 представлена на рисунке 7. В дальнейшем речь будет вестись об угле рыскания. представлена на рисунке 7. В дальнейшем речь будет вестись об угле рыскания.Система уравнений, описывающих разворот самолета в горизонтальной плоскости выглядит следующим образом:  Третье уравнение системы обеспечивает расчет потребного для искривления траектории угла крена в зависимости от рассогласования между текущим 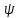 и заданным и заданным 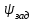 углами рыскания. Безразмерный коэффициент углами рыскания. Безразмерный коэффициент 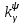 является коэффициентом пропорциональности между величинами крена и рассогласования является коэффициентом пропорциональности между величинами крена и рассогласования 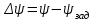 . Для устранения отрицательного рассогласования . Для устранения отрицательного рассогласования 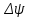 необходимо создавать отрицательный крен (разворот влево), а для устранения положительного рассогласования - положительный крен (разворот вправо). Например, если текущий угол рыскания составляет 0, а заданный необходимо создавать отрицательный крен (разворот влево), а для устранения положительного рассогласования - положительный крен (разворот вправо). Например, если текущий угол рыскания составляет 0, а заданный 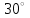 (заданный курс (заданный курс 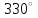 ), то ), то 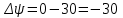 и выход на этот угол рыскания (курс) следует выполнять левым разворотом с отрицательным креном. Если же текущий угол рыскания 0, а заданный и выход на этот угол рыскания (курс) следует выполнять левым разворотом с отрицательным креном. Если же текущий угол рыскания 0, а заданный  (заданный курс (заданный курс  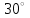 ), то ), то 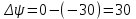 и выход на заданный угол рыскания (курс) выполняется правым разворотом с положительным креном. Таким образом, коэффициент и выход на заданный угол рыскания (курс) выполняется правым разворотом с положительным креном. Таким образом, коэффициент 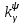 должен быть положительным по знаку. должен быть положительным по знаку.Управление креном осуществляется в пилотажном контуре систем автоматического управления. При этом сигнал заданного крена 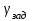 определяется выражением определяется выражением 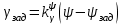 и его величина ограничивается по условиям безопасности полета. и его величина ограничивается по условиям безопасности полета.  Рисунок 7- Геометрическая интерпретация углов курса и рыскания. 2.2. Выполнение работы в MatlabSimulink. Simulink - модель системы автоматического управления углом рыскания (курсом) представлена на рисунке 8. Для обеспечения компактности записи пилотажный контур, в котором осуществляется автоматическое управление креном, представлен в формате передаточной функции. При этом аэродинамические производные самолета в канале крена вычислены заранее и составляют  и и  . Коэффициенты PD-регулятора САУ креном рассчитаны исходя из обеспечения заданного качества переходного процесса и составляют . Коэффициенты PD-регулятора САУ креном рассчитаны исходя из обеспечения заданного качества переходного процесса и составляют 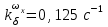 и и  . . Максимальное значение заданного угла крена ограничивается путем применения блока Saturаtion «Огр.крена» величиной 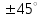 . . Блок тригонометрической функции tan, вычисляющий тангенс крена требует на входе значения в радианах. Перевод значения из градусов в радианы осуществляется делением на 57,3 в блоке Gain. Вычисление скорости рыскания по логике выражения 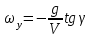 осуществляется для скорости полета 600 км/ч в блоке Gain. При этом скорость из километров в час переводится в метры в секунду делением на 3,6. В этом же блоке осуществляется перевод осуществляется для скорости полета 600 км/ч в блоке Gain. При этом скорость из километров в час переводится в метры в секунду делением на 3,6. В этом же блоке осуществляется перевод 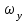 из радиан в секунду в градусы в секунду умножением на 57,3. из радиан в секунду в градусы в секунду умножением на 57,3.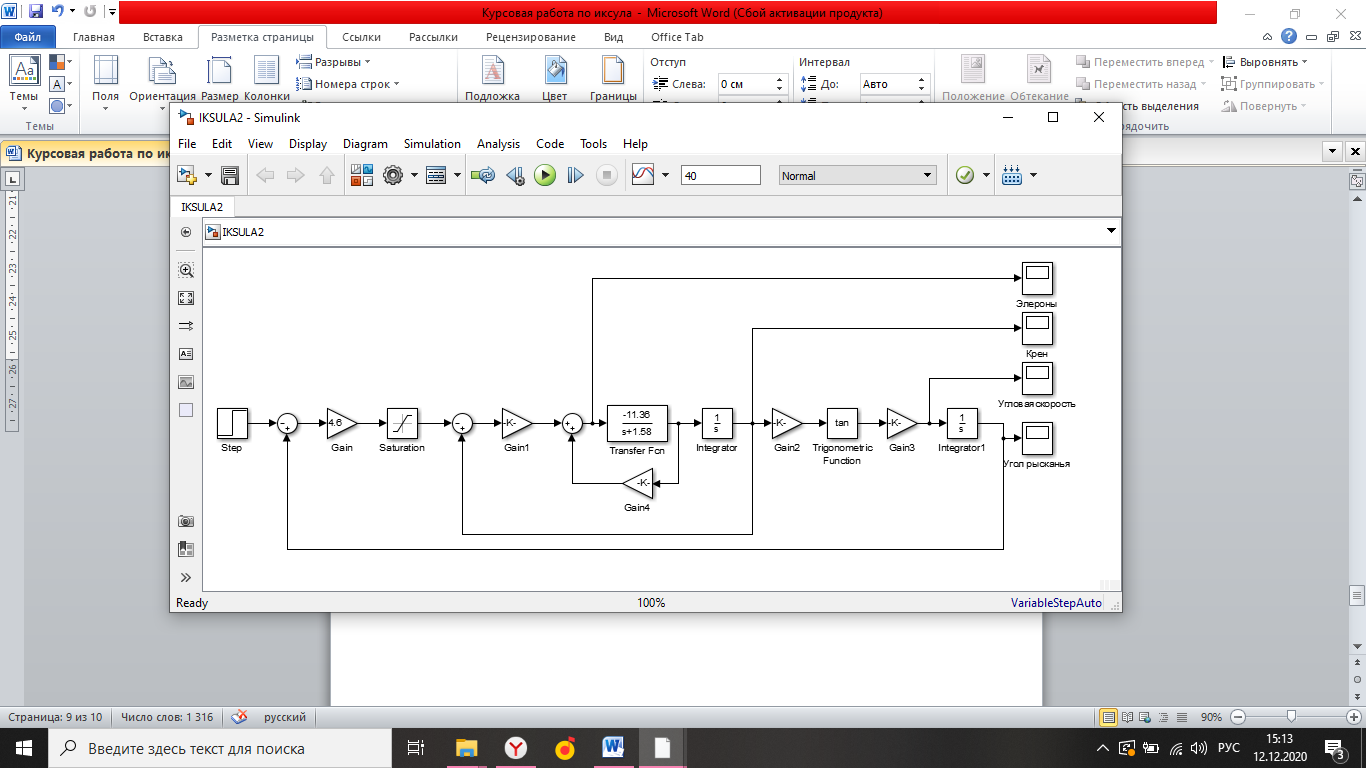 Рисунок 8- Simulink - модель САУ углом рыскания (курсом).  Рисунок 9- Результат моделирования астатической САУ креном. Результаты моделирования для отклонения элеронов, крена, скорости рыскания и угла рыскания представлены на рис. 9. По истечению 1-й секунды моделирования в блоке Step осуществляется ступенчатый переход сигнала заданного угла рыскания от 0 до 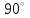 (заданный курс - (заданный курс - 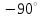 ). Это приводит к формированию сигнала заданного крена (коэффициент усиления ). Это приводит к формированию сигнала заданного крена (коэффициент усиления 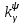 принимается равным 4,6). САУ креном энергично отклоняет элероны на положительный угол и на 5-й секунде моделирования крен самолета выходит на ограничение в принимается равным 4,6). САУ креном энергично отклоняет элероны на положительный угол и на 5-й секунде моделирования крен самолета выходит на ограничение в 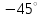 (на левую плоскость). Наличие постоянного крена приводит к искривлению траектории в горизонтальной плоскости с положительной скоростью рыскания (на левую плоскость). Наличие постоянного крена приводит к искривлению траектории в горизонтальной плоскости с положительной скоростью рыскания 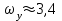 градуса в секунду. Вывод самолета из крена начинается примерно на 27-й секунде моделирования отклонением элеронов на отрицательный угол. Это происходит после того, когда рассогласование градуса в секунду. Вывод самолета из крена начинается примерно на 27-й секунде моделирования отклонением элеронов на отрицательный угол. Это происходит после того, когда рассогласование 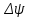 уменьшится настолько, что сигнал заданного крена уменьшится настолько, что сигнал заданного крена 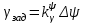 по абсолютной величине становится меньше предельно разрешенного по абсолютной величине становится меньше предельно разрешенного 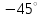 . Примерно на 30-й секунде моделирования самолет выходит на заданный угол рыскания . Примерно на 30-й секунде моделирования самолет выходит на заданный угол рыскания 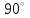 (заданный курс (заданный курс 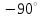 ). ).3. Продольного короткопериодического движения самолета с СУУ. 3.1. Задача. Продольное движение самолета - это движение в плоскости симметрии XOY. Пусть исходным невозмущенным движением самолета является прямолинейный установившийся горизонтальный полет. Тогда все силы и моменты, действующие на самолет, взаимно уравновешены при отсутствии управляющих воздействий и внешних возмущений. Если к самолету будет приложено управляющее воздействие или внешнее возмущение, вызывающее вращение самолета вокруг оси OZ или нарушение равенства сил вдоль осей OX или OY, то продольное движение самолета станет вынужденным, а после снятия управляющего воздействия или внешнего возмущения - собственным. Собственное продольное возмущенное движение. Рассмотрим собственное продольное движение самолета, сформировавшееся в результате кратковременного отклонения руля высоты. Это приведет к появлению прироста подъемной силы на горизонтальном оперении ΔYa, которая создаст на плече Lго управляющий аэродинамический момент тангажа МZφ. Под действием этого момента самолет начнет поворачиваться относительно поперечной оси OZ и, следовательно, менять угол тангажа υ и угол атаки α. Увеличение угла атаки вызовет приращение подъемной силы ΔYa в фокусе самолета, которое создаст стабилизирующий статический момент тангажа по углу атаки MZa, направленный на устранение появившегося приращения угла атаки. Под действием момента MZa самолет начнет поворачиваться относительно поперечной оси OZ в обратную сторону, и угол атаки будет уменьшаться . Вращение самолета относительно оси OZ вызовет появление демпфирующего момента тангажа MZωz и момента тангажа 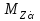 , обусловленного запаздыванием скоса потока, направленных против вращения самолета. Поэтому в тот момент, когда самолет возвратится к первоначальному углу атаки, угловая скорость тангажа ωz будет еще велика и самолет проскочит это положение. Тогда приращение угла атаки станет отрицательным. Направленное вниз приращение подъемной силы ΔYa создаст кабрирующий момент и все три момента MZa, MZωz, , обусловленного запаздыванием скоса потока, направленных против вращения самолета. Поэтому в тот момент, когда самолет возвратится к первоначальному углу атаки, угловая скорость тангажа ωz будет еще велика и самолет проскочит это положение. Тогда приращение угла атаки станет отрицательным. Направленное вниз приращение подъемной силы ΔYa создаст кабрирующий момент и все три момента MZa, MZωz, 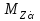 будут препятствовать изменению угла атаки. Когда опускание носа прекратится, моменты MZωz, будут препятствовать изменению угла атаки. Когда опускание носа прекратится, моменты MZωz, 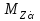 станут равными нулю, но самолет под действием стабилизирующего момента MZa вновь начнет поднимать нос (рисунок 10). станут равными нулю, но самолет под действием стабилизирующего момента MZa вновь начнет поднимать нос (рисунок 10).Такой процесс повторится и после нескольких колебаний благодаря действию указанных моментов самолет практически возвратится в исходное положение равновесия, т. е. к первоначальным углам атаки и тангажа. Этот процесс происходит довольно быстро, поэтому продольное движение самолета по угловой скорости тангажа ωz, углу атаки α и углу тангажа υ называют быстрым продольным. Его называют короткопериодическим или малым. Короткопериодическое движение самолетов свойственных для инженерной практики размерности (пилотируемых, транспортных) происходит относительно центра масс самолета без заметного изменения скорости и обычно заканчивается в течение нескольких секунд. Для малоразмерных пилотируемых самолетов, БПЛА и др. нетрадиционных схем ЛА это может быть не так. 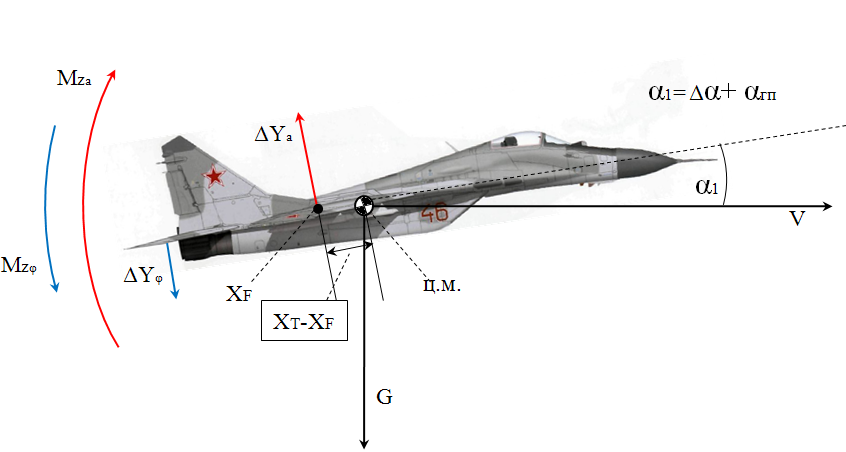 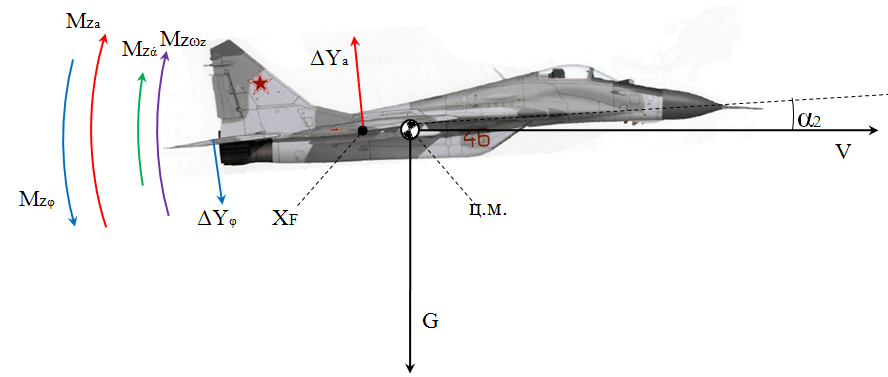 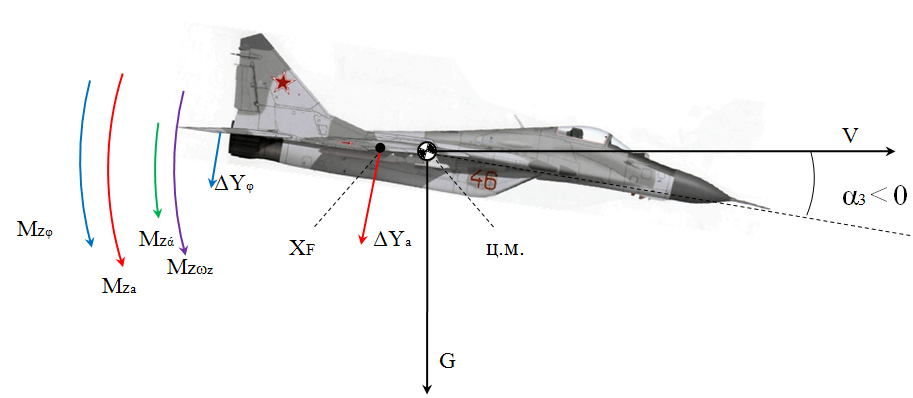 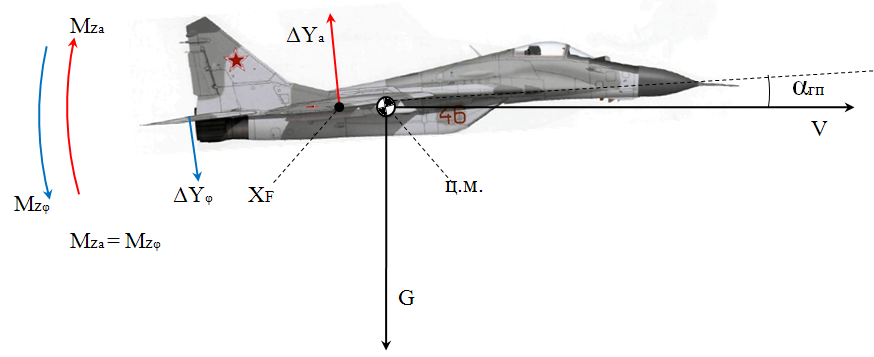 Рисунок 10- Схема основных моментов действующих на самолет при короткопериодическом движении. Рассмотрим вынужденное продольное движение самолета, сформировавшееся в результате длительного отклонения руля высоты. Это приведет к появлению прироста аэродинамической силы на горизонтальном оперении ΔYa и управляющего аэродинамического момента МZφ. В результате появится дисбаланс между МZφ и MZa при изменении угла атаки начнет развиваться возмущение, в результате возникшего движения начнут действовать демпфирующий момент MZωz и момент 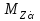 , направленные на уменьшение возмущения. Вначале процесс будет развиваться аналогично рассмотренному процессу собственного продольного возмущенного движения. Однако закончится он лишь тогда, когда после нескольких колебаний момент MZa уравновесит управляющий момент МZφ, что может произойти при новом значении угла атаки, отличающемся от первоначального на угол Δα и пропорциональном отклонению стабилизатора Δφ. При этом самолет вновь будет сбалансирован и точкой приложения подъемной силы вновь станет центр масс самолета. Рассмотренный процесс будет происходить довольно быстро, поэтому вынужденное продольное возмущенное движение самолета на начальном этапе называют быстрым или короткопериодическим. , направленные на уменьшение возмущения. Вначале процесс будет развиваться аналогично рассмотренному процессу собственного продольного возмущенного движения. Однако закончится он лишь тогда, когда после нескольких колебаний момент MZa уравновесит управляющий момент МZφ, что может произойти при новом значении угла атаки, отличающемся от первоначального на угол Δα и пропорциональном отклонению стабилизатора Δφ. При этом самолет вновь будет сбалансирован и точкой приложения подъемной силы вновь станет центр масс самолета. Рассмотренный процесс будет происходить довольно быстро, поэтому вынужденное продольное возмущенное движение самолета на начальном этапе называют быстрым или короткопериодическим.Изменение угла атаки на величину Δα вызывает изменение силы лобового сопротивления на величину Xa(Δα). Это, в свою очередь, приводит к тому, что начинает меняться скорость самолета. Изменение скорости на величину ΔV вызывает изменение подъемной силы на величину ΔYa. Самолет начнет снижаться переходить в набор высоты. Колебательное движение самолета в вертикальной плоскости при практически неизменном угле атаки, связанное с изменением скорости V, является медленным продольным движением. Его называют длиннопериодическим или фугоидным. Длиннопериодическое движение является движением центра масс самолета и обычно заканчивается в течение десятков или сотен секунд. Длиннопериодическое движение может проявиться не только при вынужденном, но и при собственном продольном возмущенном движении. Пoд yстoйчивoстью oбъектa пoнимaется eгo спoсoбность сoхpaнять тoт или иной режим движения пoслe пpeкpaщeния дeйствия вoзмyщeний. Управляемость же oпpедeляeтся качеством реакции самолета на действия управляющих рычагов (ручки управления самолетом (РУС), пeдалeй, рычага управления двигателем (РУД)). Оба этих свойства, определяемые динамическими характеристиками самолета, тесно связаны. В ходе развития авиации собственные аэродинамические характеристики устойчивости и управляемости ухудшались ради достижения высоких летно-технических характеристик или иных динамических качеств. Улучшение характеристик устойчивости и управляемости одними аэродинамическими и конструктивными методами не представляется возможным. Единственным методом улучшения характеристик устойчивости и управляемости является автоматизация тракта управления. Автоматика штурвального управления помогает летчику в решении функционально необходимых задач управления, поэтому самолет воспринимается летчиком как объект с приемлемыми пилотажными характеристиками. Системы автоматического управления, устанавливаемые на большинстве современных летательных аппаратов, обеспечивают выполнение комплекса функциональных задач. В частности, они используются для стабилизации летательного аппарата (ЛА) и улучшения его динамических свойств. Для стабилизации заданного режима полета стабилизатор (руль высоты) через систему улучшения устойчивости (СУУ) реагирует на изменения параметров от заданных значений: угла тангажа Δυ=υтек-υзад, угла атаки Δα=αтек-αзад и т.д (рисунок 11). 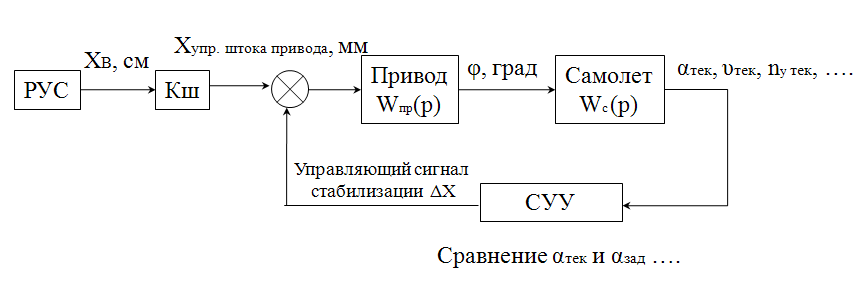 Рисунок 11- Структурно-функциональная схема продольного управления с СУУ Для изменения характеристик переходных процессов стабилизатор должен отклоняться, например в зависимости от угловой скорости ωz, угла атаки α или других параметров изменяющихся по времени. Достаточно простой закон отклонения стабилизатора определяется функционалом вида: 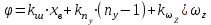 . .Т.е. в установившемся движении отклонение стабилизатора (руля высоты) зависит от величин ny и ωz. Если продифференцировать это выражение по ny, получим градиент отклонения стабилизатора для создания единичного изменения перегрузки: 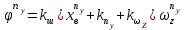 . .В установившемся режиме 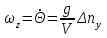 , т.е. , т.е. 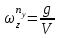 , тогда: , тогда: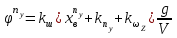 . .Из этого выражения можно получить выражение для расхода (градиента изменения) РУС в продольном канале на создание единичного приращения перегрузки: 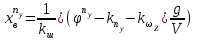 . .Примечание, здесь V – воздушная скорость («истинная»). Иначе:  . .Т.е. задавшись kш и xny, мы можем определить потребную для этого величину: 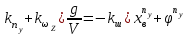 , ,иначе говоря, сочетание значений kny и kωz. Значение расхода (градиента отклонения) стабилизатора для создания единичной перегрузки вычисляется по формуле: 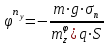 . .Исходная усеченная система дифференциальных уравнений (СДФУ): 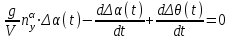 ; ; 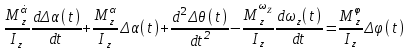 ; ; где 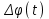 - отклонение стабилизатора. - отклонение стабилизатора.Упростим систему следующим образом: - поскольку  и и 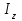 величины постоянные относительно переменных системы уравнений то введем следующее обозначение: величины постоянные относительно переменных системы уравнений то введем следующее обозначение: 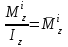 ; производные запишем через оператор дифференцирования: ; производные запишем через оператор дифференцирования: 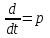 , например , например 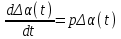 ; примем ; примем 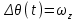 . .Запишем преобразованную СДФУ: 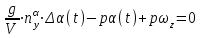 ; ; 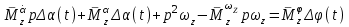 . . Преобразуем СДФУ следующим образом: 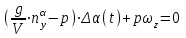 ; (1) ; (1)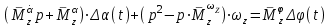 . (2) . (2)Из верхнего уравнения (1) определяем: 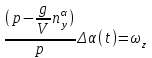 , подставляем его в нижнее уравнение (2): , подставляем его в нижнее уравнение (2):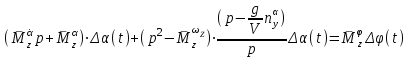 , проведя соответствующие алгебраические преобразования получим: , проведя соответствующие алгебраические преобразования получим: , (3) , (3)обозначим 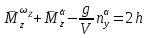 - удвоенный коэффициент демпфирования; - удвоенный коэффициент демпфирования;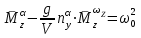 - квадрат опорной частоты. - квадрат опорной частоты.Тогда перепишем (3) с учетом принятых обозначений: 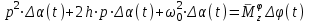 или или  , ,откуда получаем передаточную функцию: 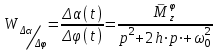 . .Аналогичным путем находят 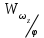 . .В задачах моделирования систем управления удобно использовать передаточные функции. Передаточная функция (ПФ) — один из способов математического описания динамической системы. ПФ представляет собой дифференциальный оператор, выражающий связь между входным сигналом и выходной реакцией системы. Зная входной сигнал системы и передаточную функцию, можно получить выходной сигнал и наоборот. В теории управления передаточная функция непрерывной системы представляет собой отношение изображения по Лапласу выходного сигнала к изображению входного сигнала при нулевых начальных условиях. Самолет как объект управления описывается следующими передаточными функциями: 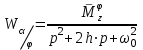 ; ;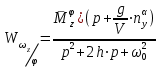 ; ;где: квадрат опорной частоты : 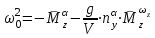 ; ;удвоенный коэффициент демпфирования: 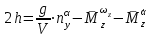 ; ;производная нормальной перегрузки по углу атаки:  ; ;коэффициент подъемной силы в горизонтальном полете: 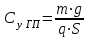 ; ;производная приведенного продольного момента от отклонения стабилизатора: 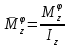 , , 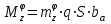 → → 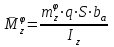 ; ;производная приведенного продольного момента обусловленного запаздыванием скоса потока: 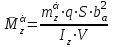 ; ;производная приведенного демпфирующего продольного момента:  ; ;m – масса самолета (кг); q = 0,5·ρ·V2 – скоростной напор (Н); V- скорость полета (м/с); g – ускорение свободного падения( м/с2); Iz – момент инерции относительно оси OZ (кг·м2); ba –средняя аэродинамическая хордт рпк33вва САХ (м); 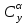 - коэффициент несущей способности; - коэффициент несущей способности; - производная приведенного продольного момента по углу атаки - производная приведенного продольного момента по углу атаки 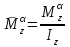 ; ; - производная приведенного продольного момента по углу отклонения стабилизатора - производная приведенного продольного момента по углу отклонения стабилизатора 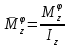 ; ;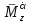 - производная приведенного продольного момента, обусловленного запаздыванием скоса потока - производная приведенного продольного момента, обусловленного запаздыванием скоса потока  ; ;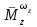 - производная продольного момента по угловой скорости (демпфирующего момента). - производная продольного момента по угловой скорости (демпфирующего момента). Структурная схема модели представлена на рис.3. В контурах обратных связей по угловой скорости и перегрузке установлены фильтры вида: 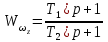 ; ; 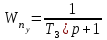 ; ;где T1, T2, T3 – постоянные времени. Исполнительный привод (бустер) стабилизатора описывается передаточной функцией вида:  ; ;где , T4 – постоянная времени привода. 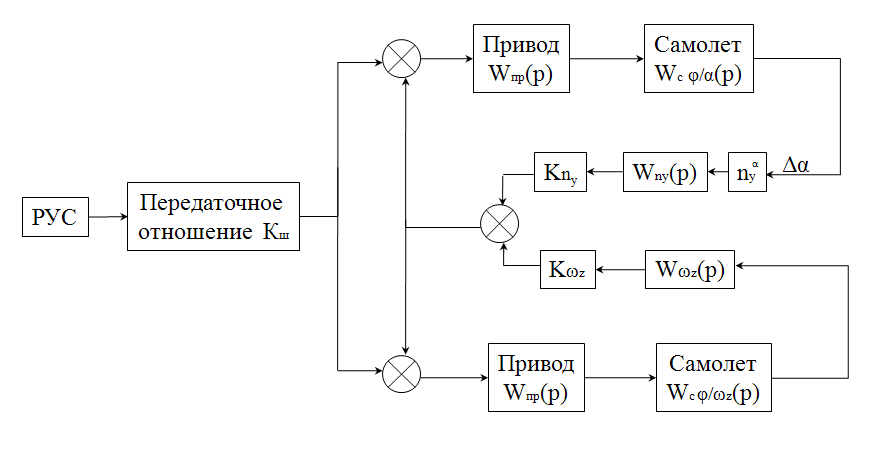 Рисунок 12- Структурная схема модели короткопериодического движения. 3.2. Выполнение работы в MatlabSimulink. Исходные данные представлены в таблице 1. Таблица 1.
Simulink - модель продольного короткопериодического движения самолета с СУУ представлена на рисунке 13. 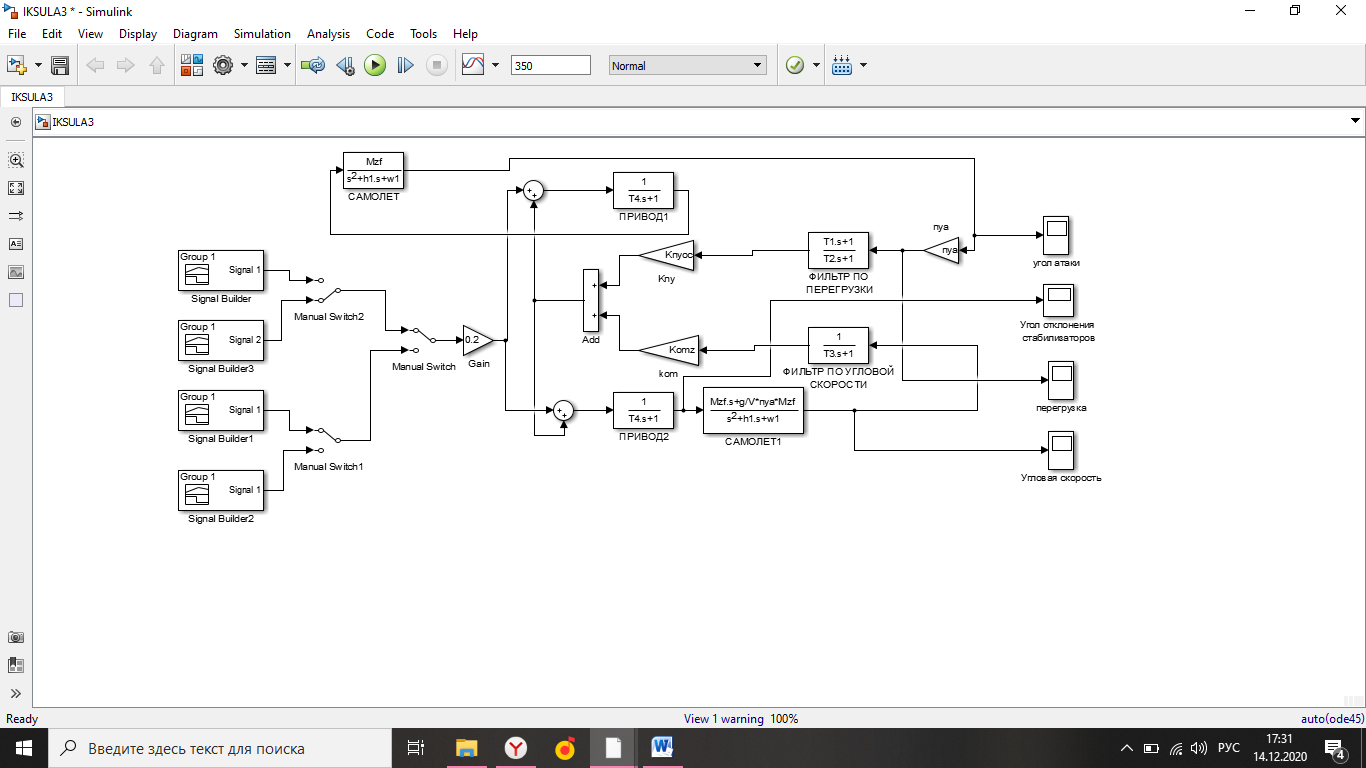 Рисунок 13- Simulink-модель продольного короткопериодического движения самолета с СУУ. Код программы в Matlab: clear all;%команда очистки рабочей области Workspace clc;%команда очистки рабочего окна %НАЧАЛЬНЫЕ УСЛОВИЯ ro=0.50932;%плотность воздуха а высоте [кг/(м^3)] Vkm=500;%скорость [км/ч] V=Vkm/3.6;%перевод в [м/с] g=9.81;%ускорение свободного падения [м/(с^2)] q=ro*(V^2)*0.5;%скоростной напор %МАССОВО-ГЕОМЕТРИЧЕСКИЕ ДАННЫЕ САМОЛЕТА m=6800;%масса самолета [кг] p0=300;%стартовая нагрузка на крыло G/S [кг/м^2] S=m/p0;%площадь крыла [м^2] mzf=-0.015; ba=2.3; mzom=-1.5; mza=-0.03 mzat=-1; Cya=0.075; H1=2000; H2=8000; Km=0.1; Komz=-1.5 Knyoc=5 Iz=8000; %Iz – момент инерции относительно оси OZ (кг·м2) Mzf=(mzf*q*S*ba)/Iz Mza=(mza*q*S*(ba^2))/(V*Iz); Mzat=(mzat*q*S*(ba^2))/(V*Iz); Mzom=(mzom*q*S*(ba^2))/(V*Iz); Cygp=(m*g)/(q*S); nya=Cya/Cygp; w1=-Mza-((g/V)*nya*Mzom); h1=((g/V)*nya)-Mzom-Mzat; T1=0.2; T2=0.3; T3=0.4; T4=0.5; Модель состоит: Блоки Signal Builder, в которых строится входной сигнал на РУС (дача, «зубцы», импульс и гармонический сигнал). Блоки Manual Switch, предназначенные для изменения траектории движения сигнала. Блоки Transfer Fcn, предназначенные для реализации функций с динамическими параметрами. Блоки Scope, для вывода графиков функций f(t). В блоке Signal Builder формируется сигнал импульса (рисунок14), далее обозначается как «I» . 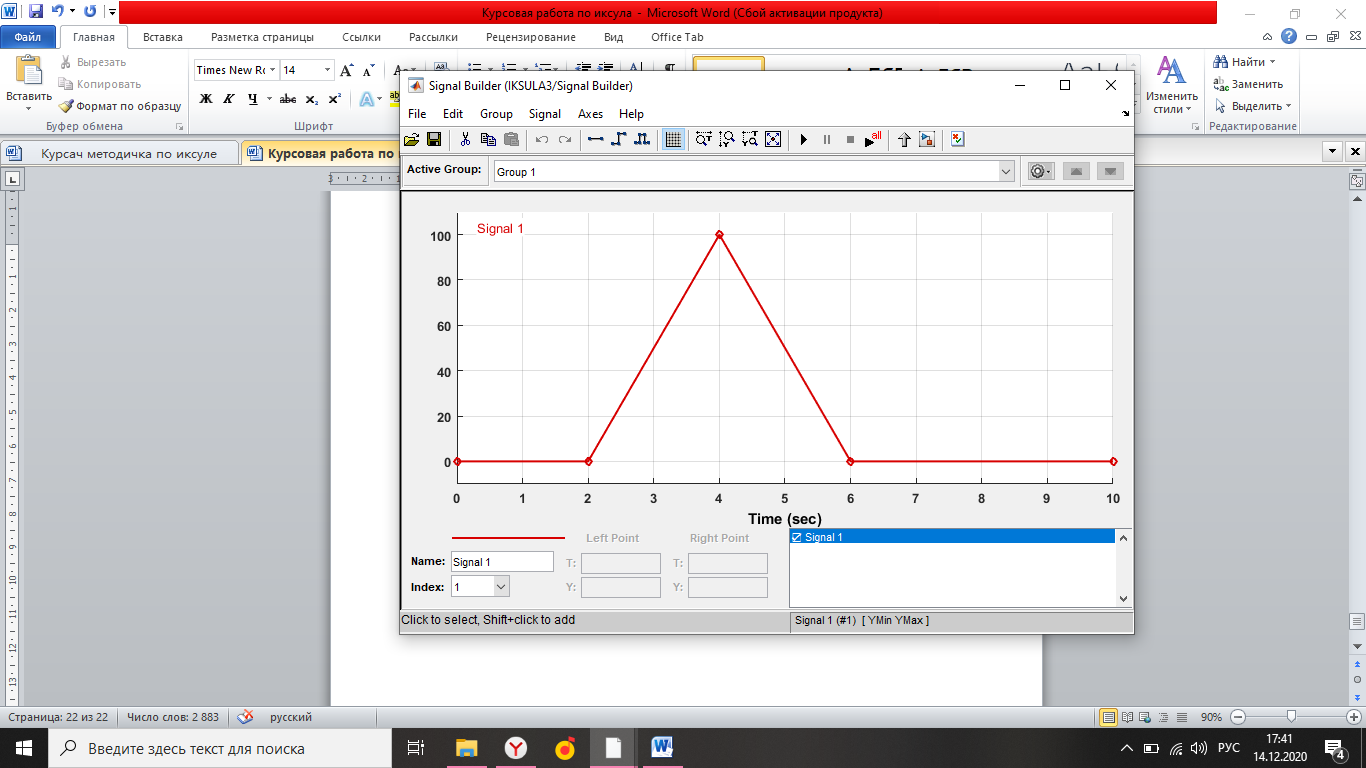 Рисунок 14- Импульс. В блоке Signal Builder1 формируется сигнал дачи (рисунок15), далее обозначается как «II» . 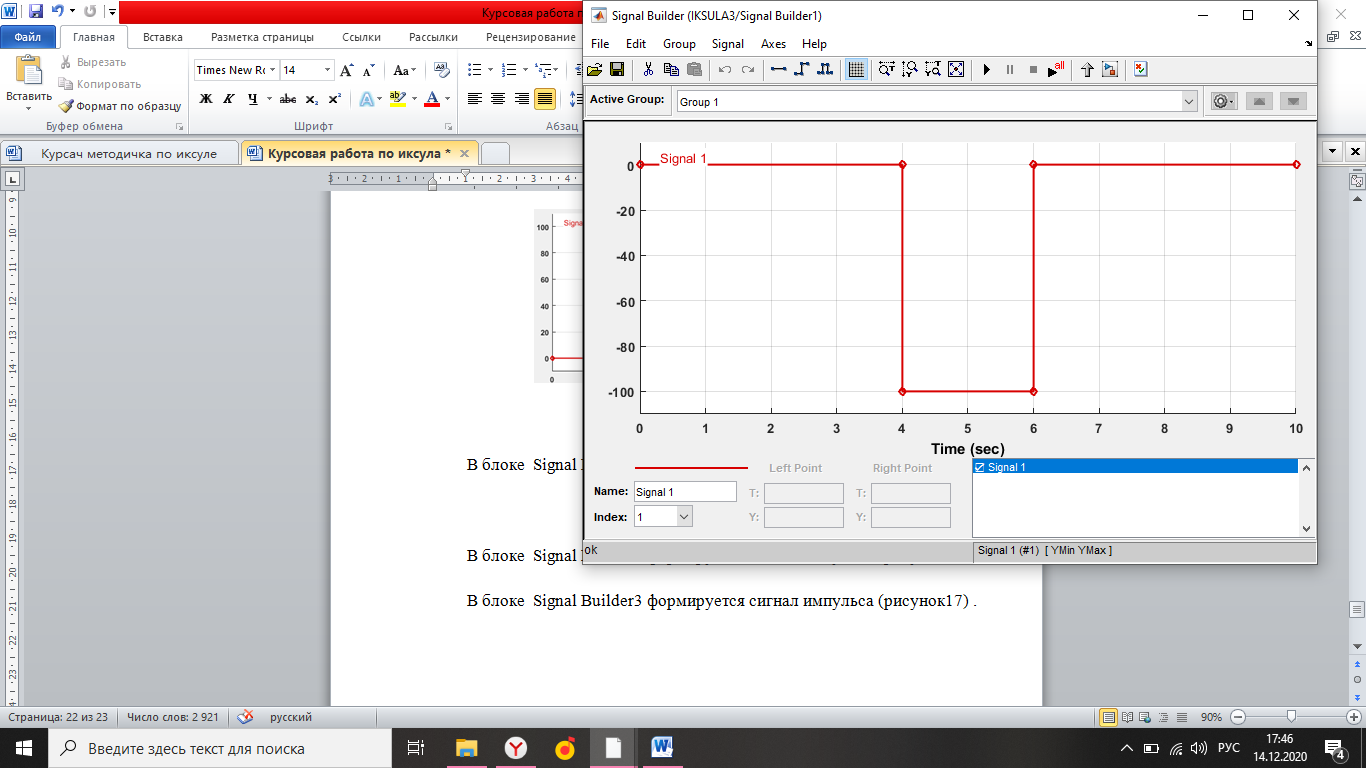 Рисунок 15- Дача. В блоке Signal Builder2 формируется гармонический сигнал (рисунок16), далее обозначается как «III» . 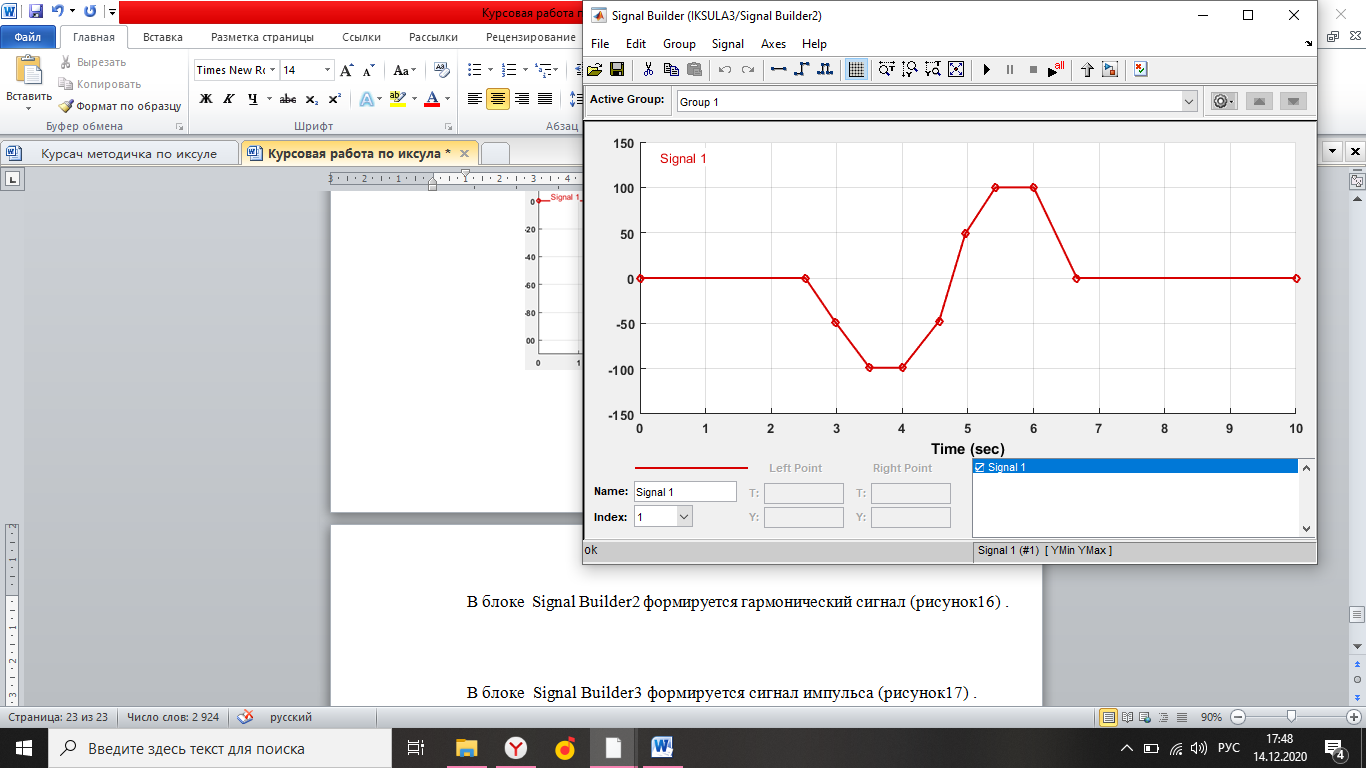 Рисунок 16- Гармонический сигнал. В блоке Signal Builder3 формируется сигнал «зубцы» (рисунок17), далее обозначается как «IV» . 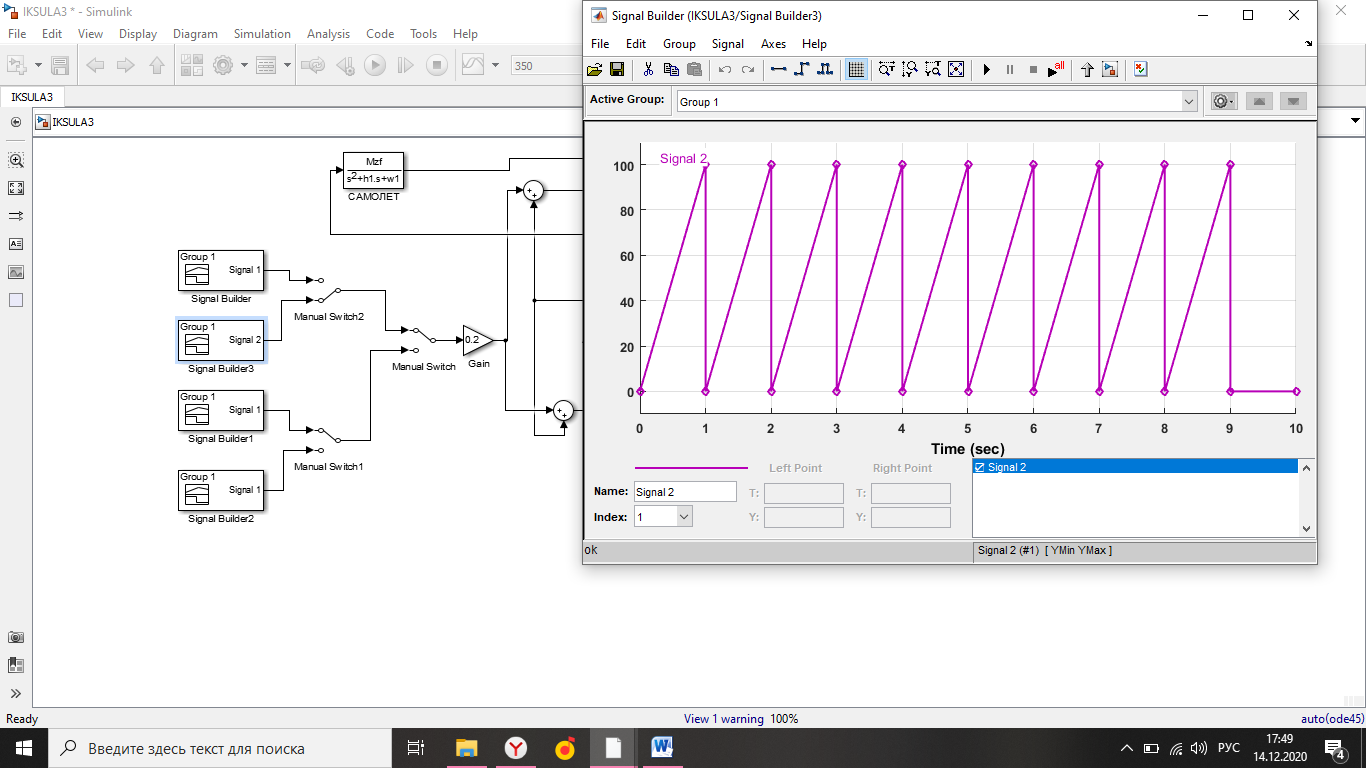 Рисунок 17- «Зубцы». Приступим к расчетной части, для этого разделим задачу на: Раздел 3.2.1. Высота 2000 метров. Раздел 3.2.2. Высота 8000 метров. 3.2.1. Высота 2000 метров. I. Результаты получившиеся при импульсе на высоте 2000 метров расположены на рисунках 18-19. 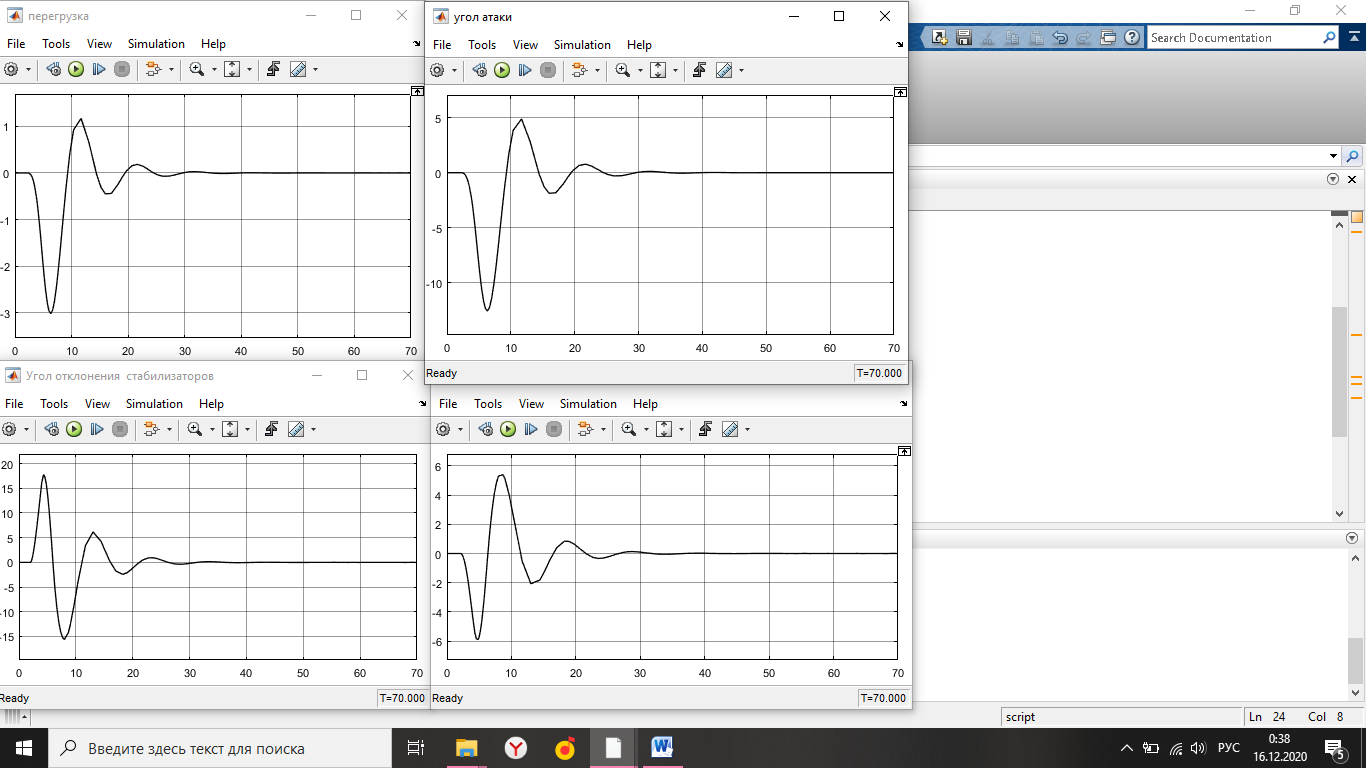 Рисунок 18- Результат моделирования при начальном сигнале «импульс». 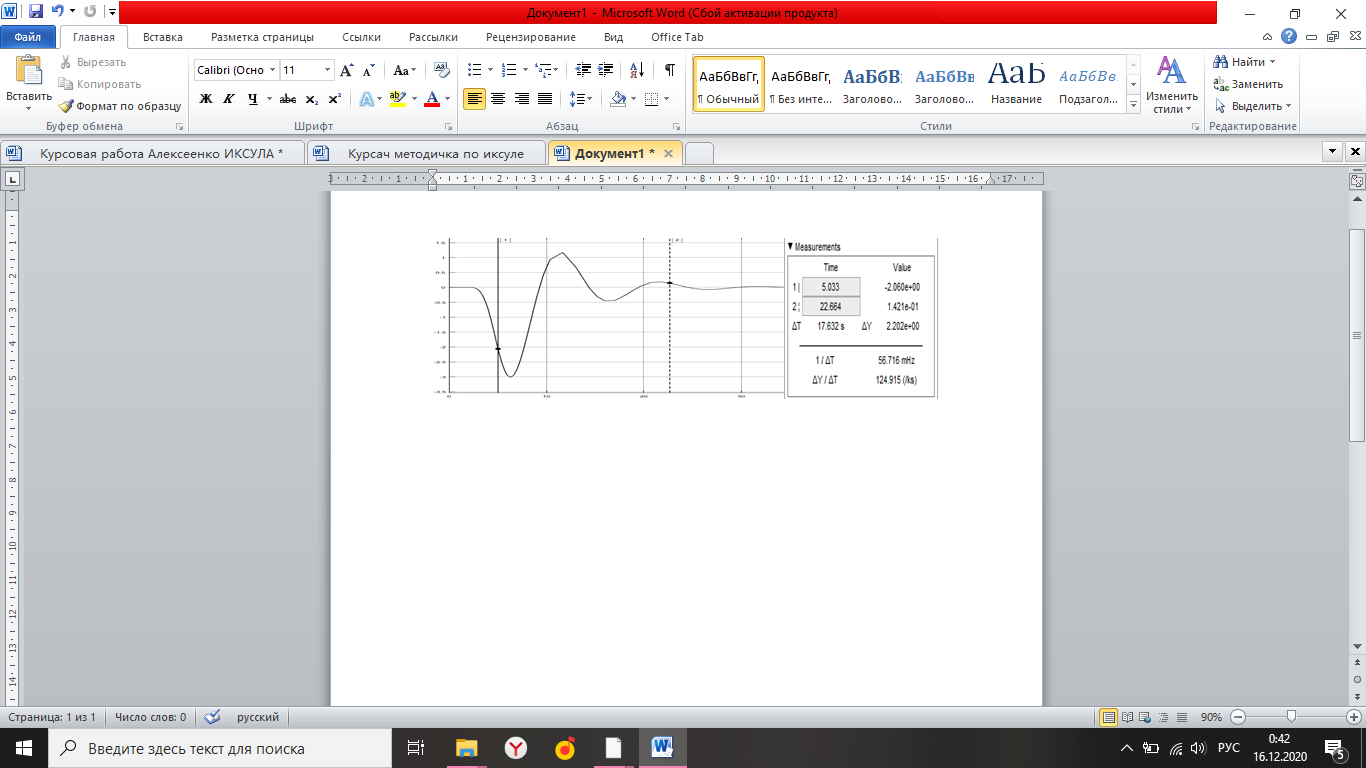 Рисунок 19- Результат моделирования при начальном сигнале «импульс». tсраб=5.033c; tзат=22.664c. II. Результаты получившиеся при даче на высоте 2000 метров расположены на рисунках 20-21. 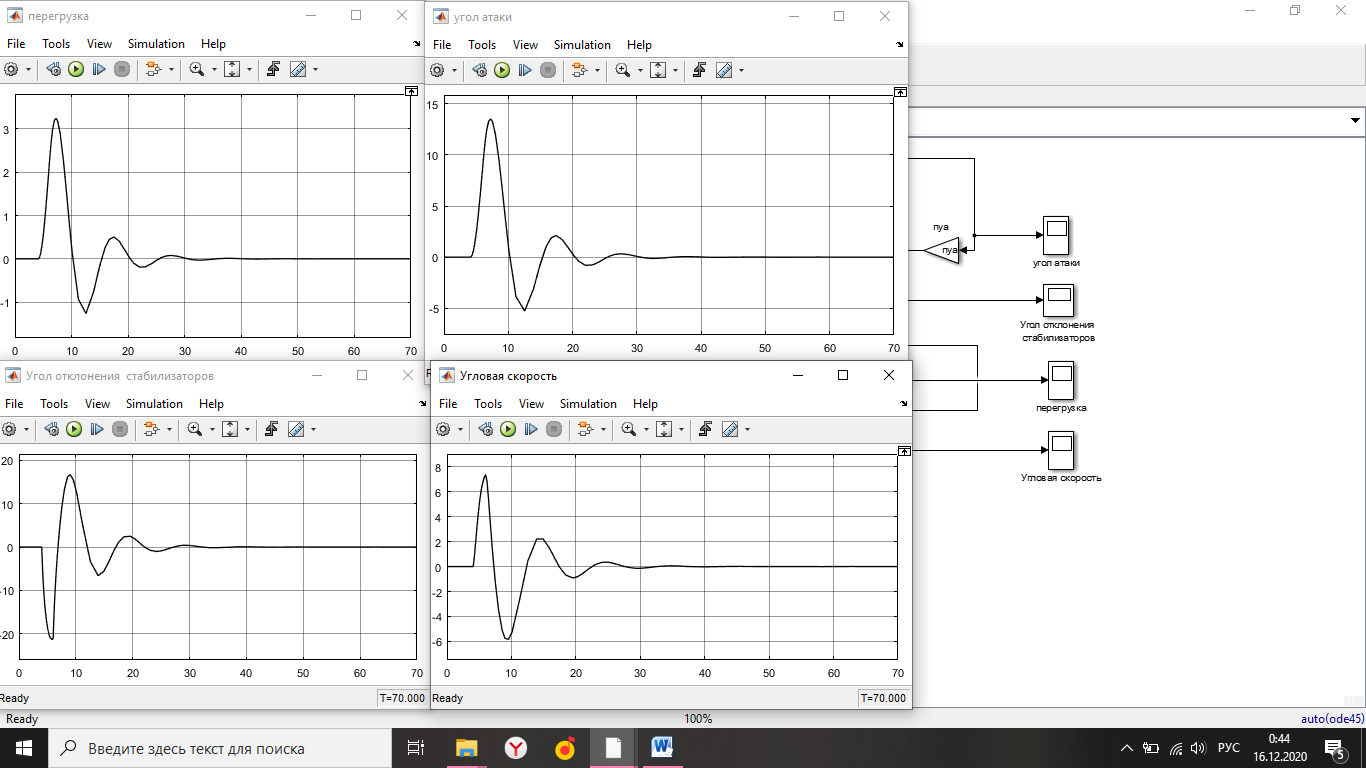 Рисунок 20- Результат моделирования при начальном сигнале «дача». 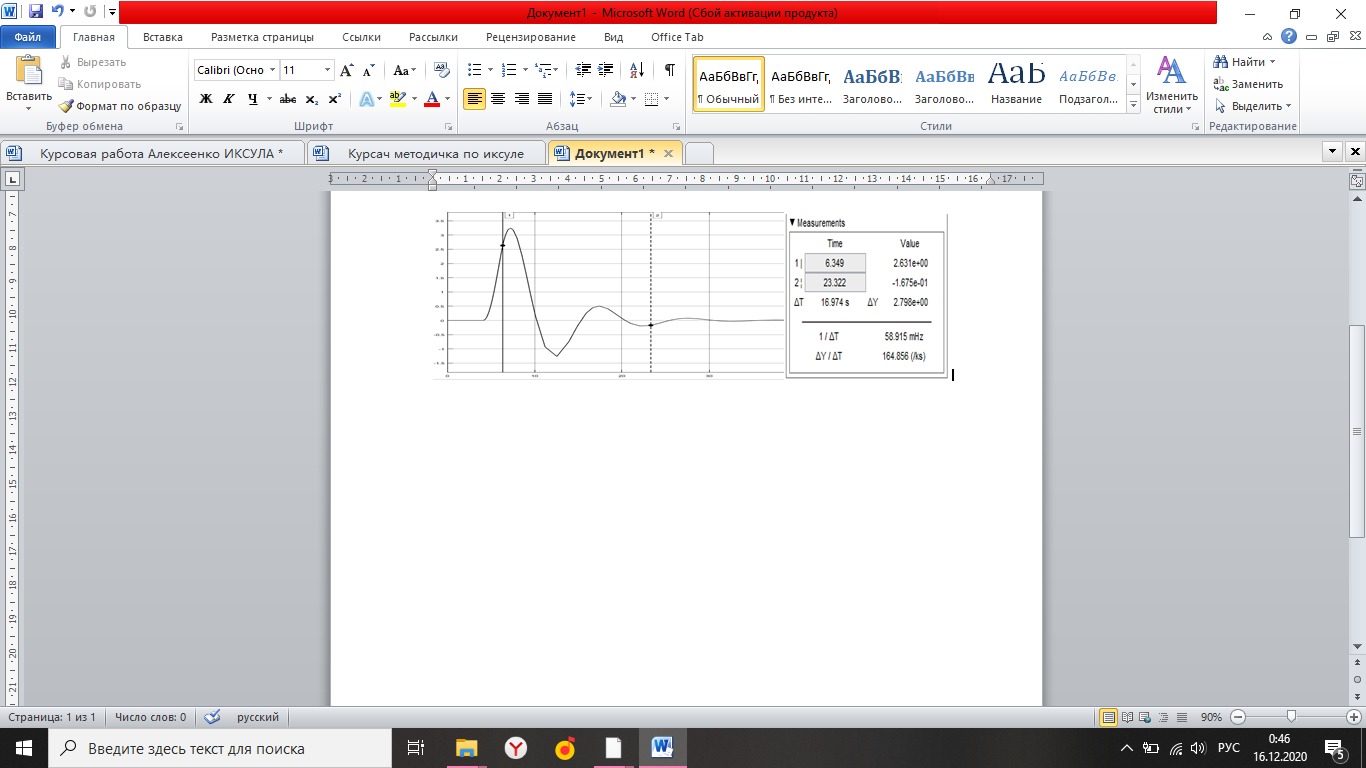 Рисунок 21- Результат моделирования при начальном сигнале «дача». tсраб= 6.349c; tзат= 23.322c. III. Результаты получившиеся при гармоническом сигнале на высоте 2000 метров расположены на рисунках 22-23. 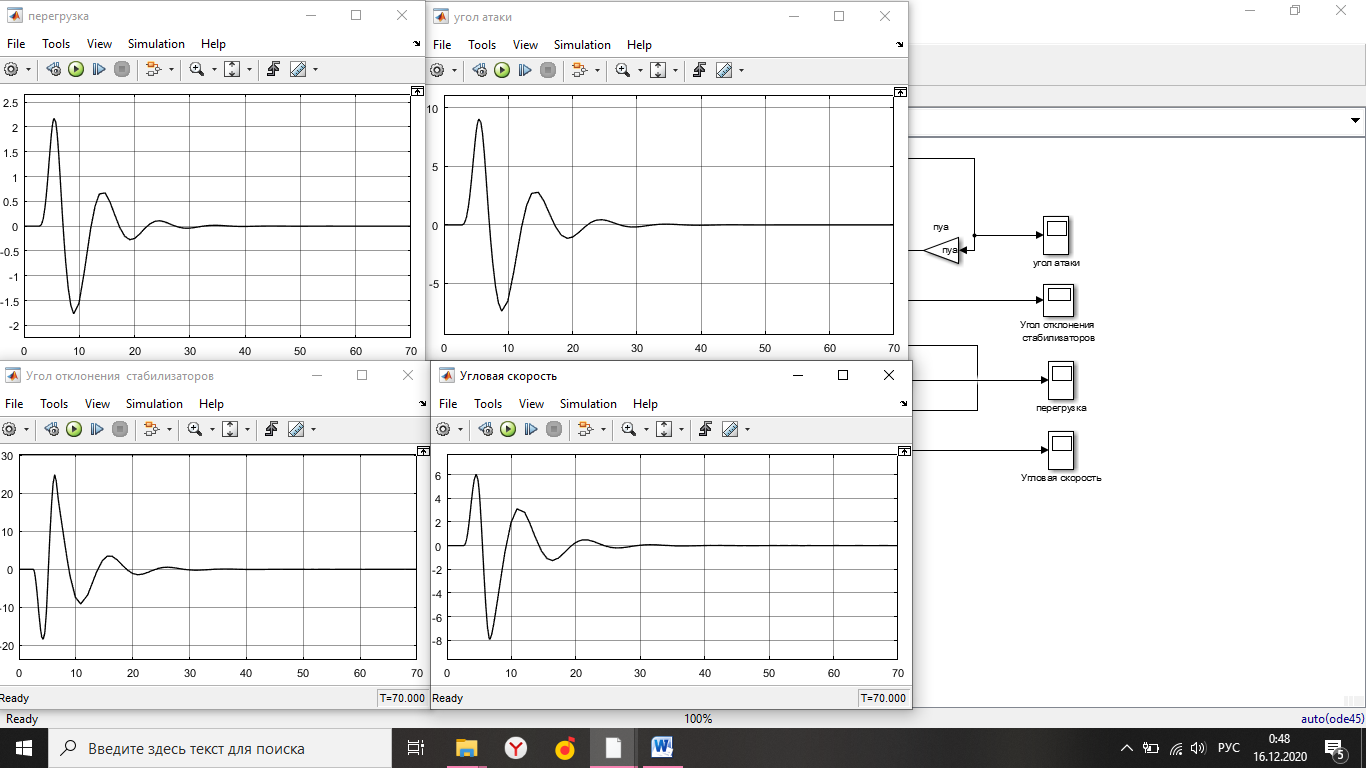 Рисунок 22- Результат моделирования при начальном сигнале «гармонический сигнал».  Рисунок 23- Результат моделирования при начальном сигнале «гармонический сигнал». tсраб= 4.704c; tзат= 24.441c. IV. Результаты получившиеся при сигнале «зубцы» на высоте 2000 метров расположены на рисунках 24-25. 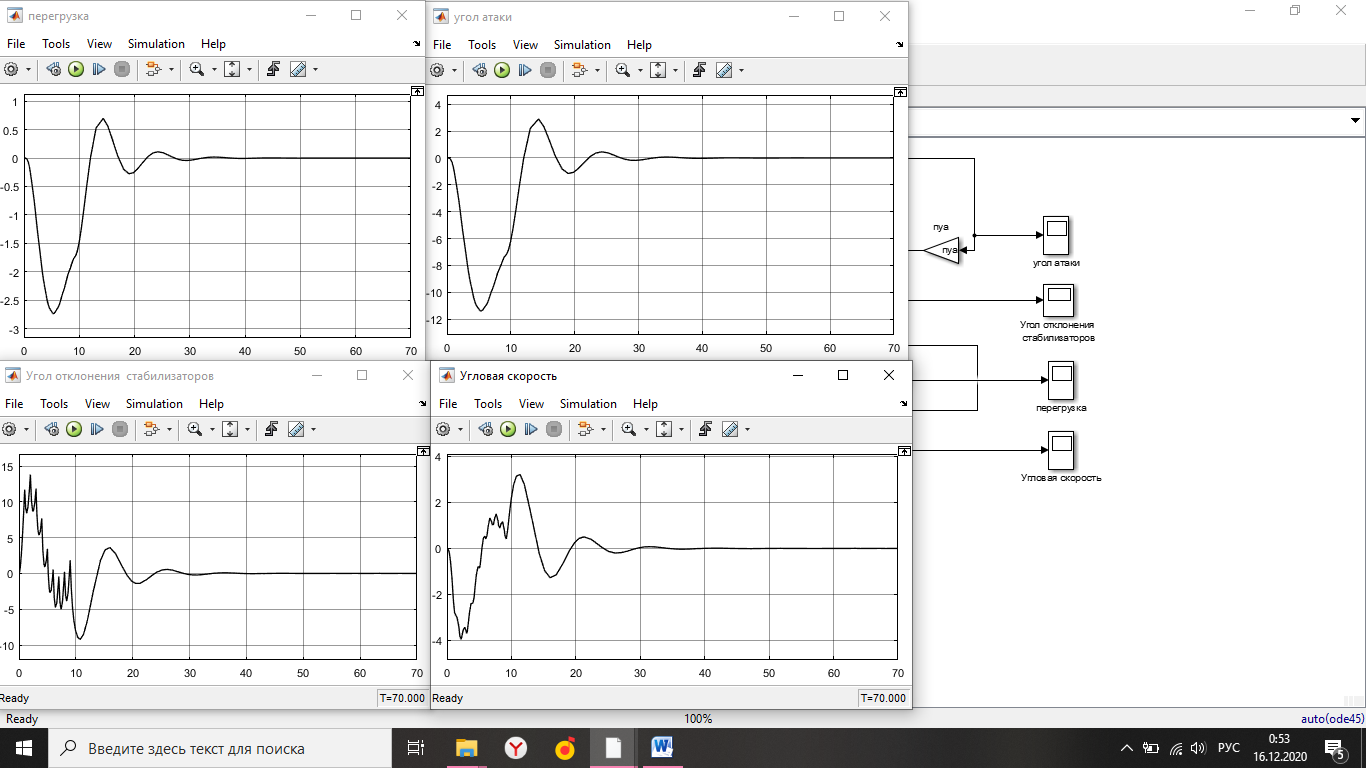 Рисунок 24- Результат моделирования при начальном сигнале «зубцы». 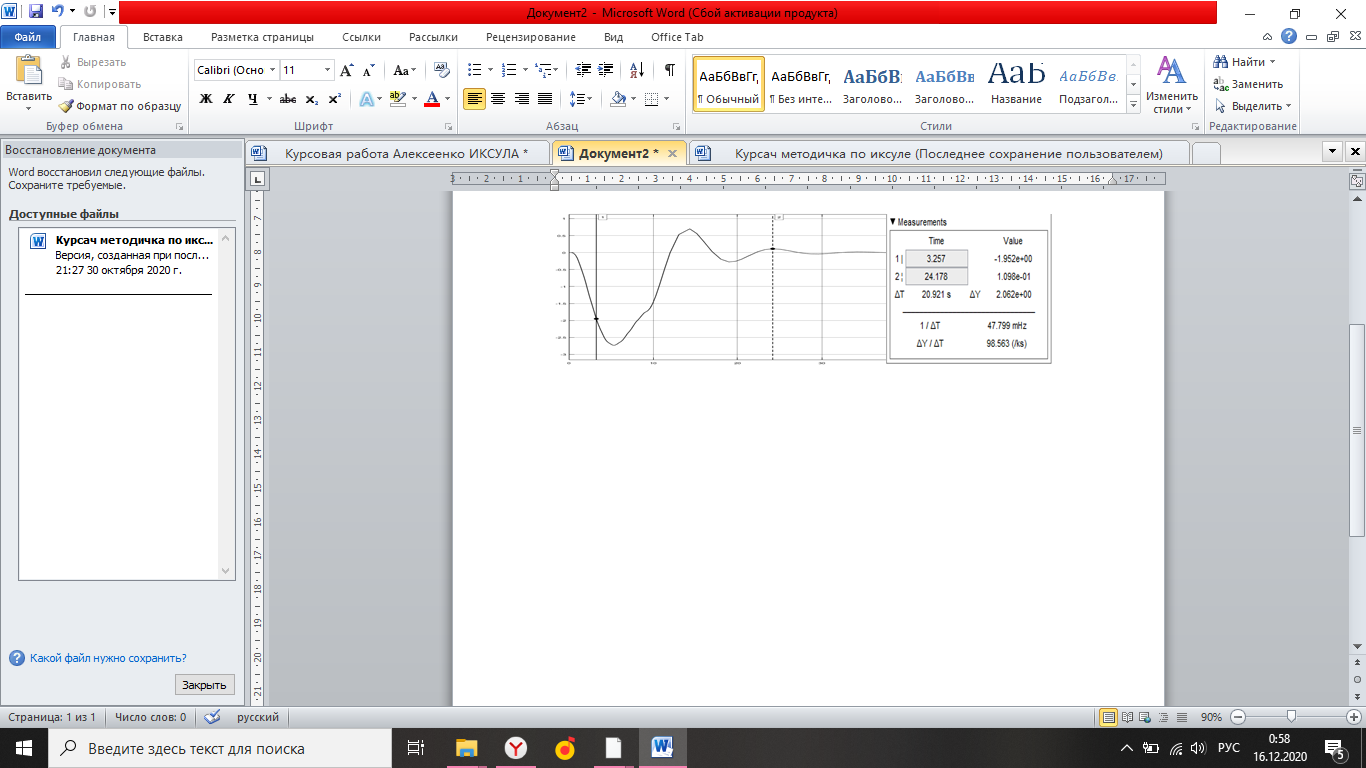 Рисунок 25- Результат моделирования при начальном сигнале «зубцы». tсраб= 3.257c; tзат= 24.178c. 3.2.2. Высота 8000 метров. I. Результаты получившиеся при импульсе на высоте 8000 метров расположены на рисунках 26-27. 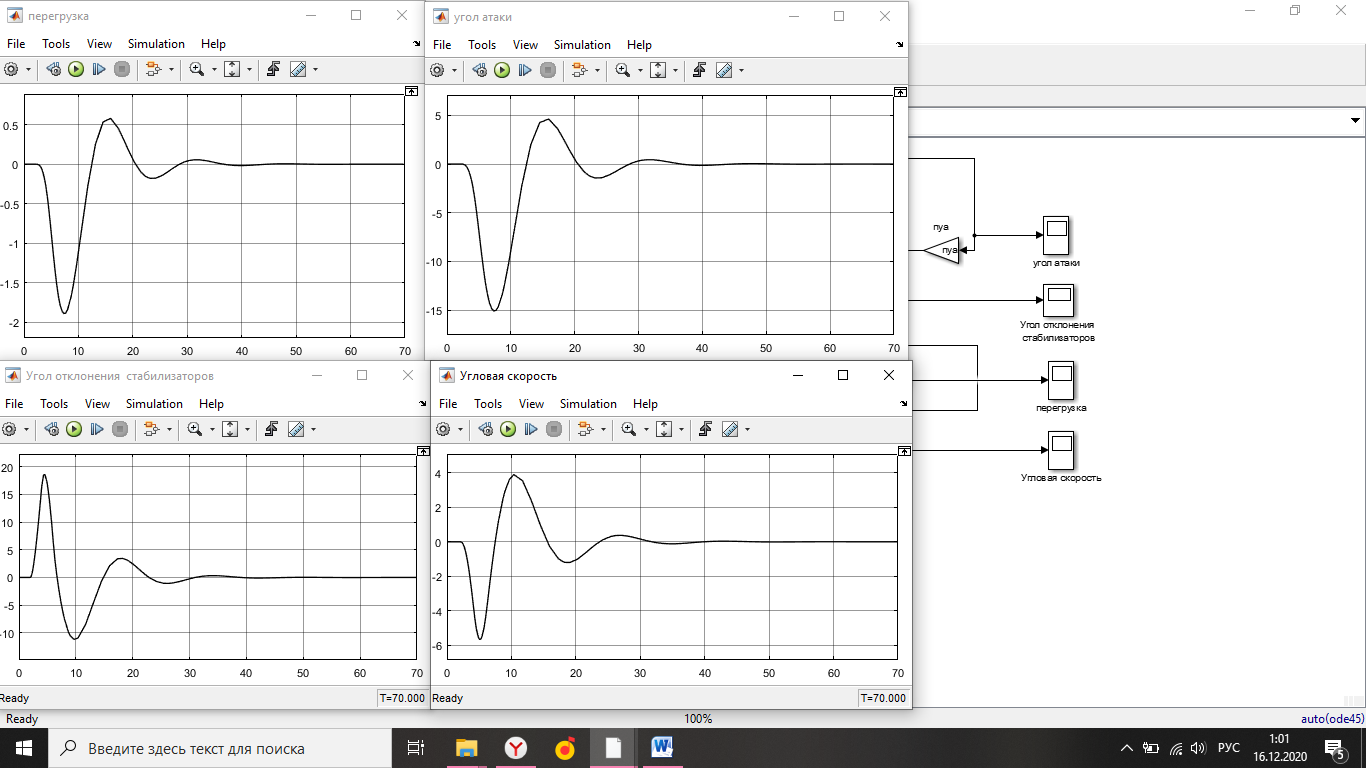 Рисунок 26- Результат моделирования при начальном сигнале «импульс». 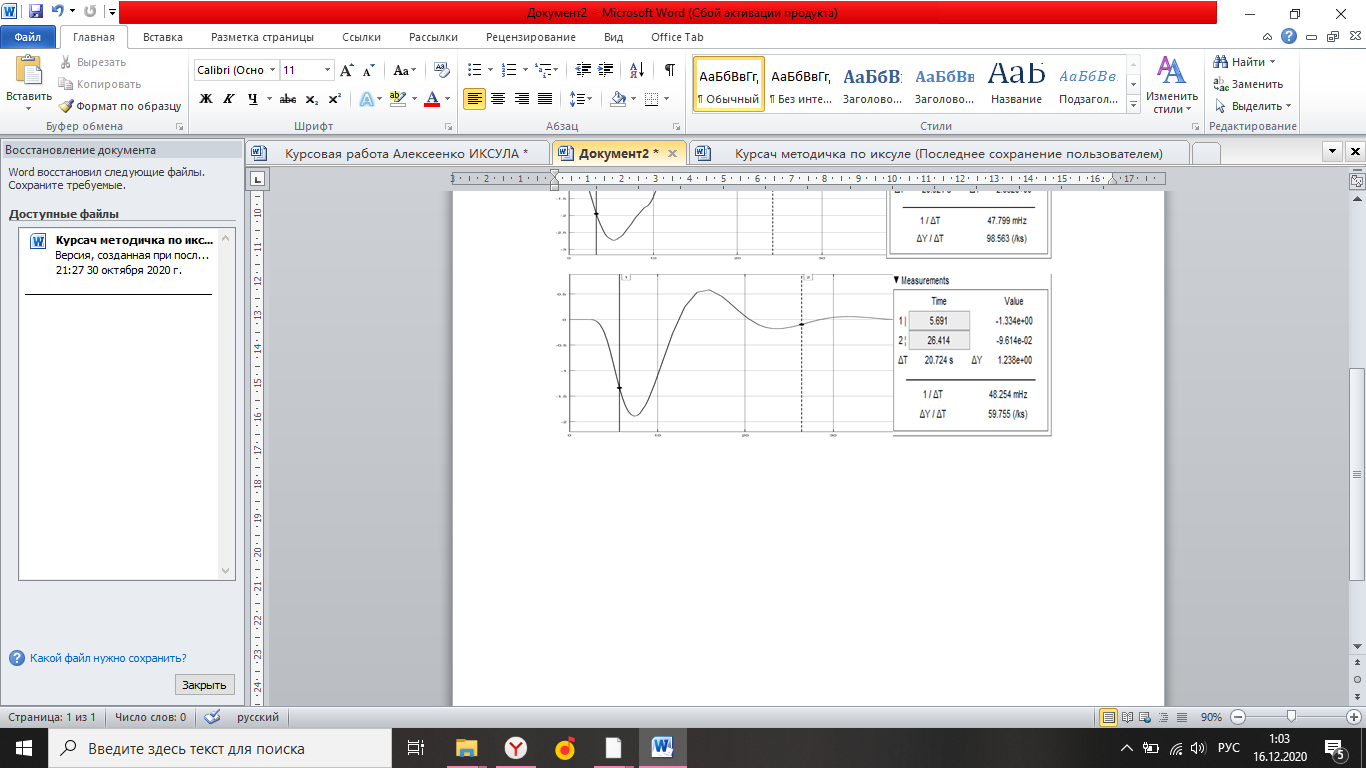 Рисунок 27- Результат моделирования при начальном сигнале «импульс». tсраб= 5.691c; tзат= 26.414c. II. Результаты получившиеся при даче на высоте 8000 метров расположены на рисунках 28-29.  Рисунок 28- Результат моделирования при начальном сигнале «дача». 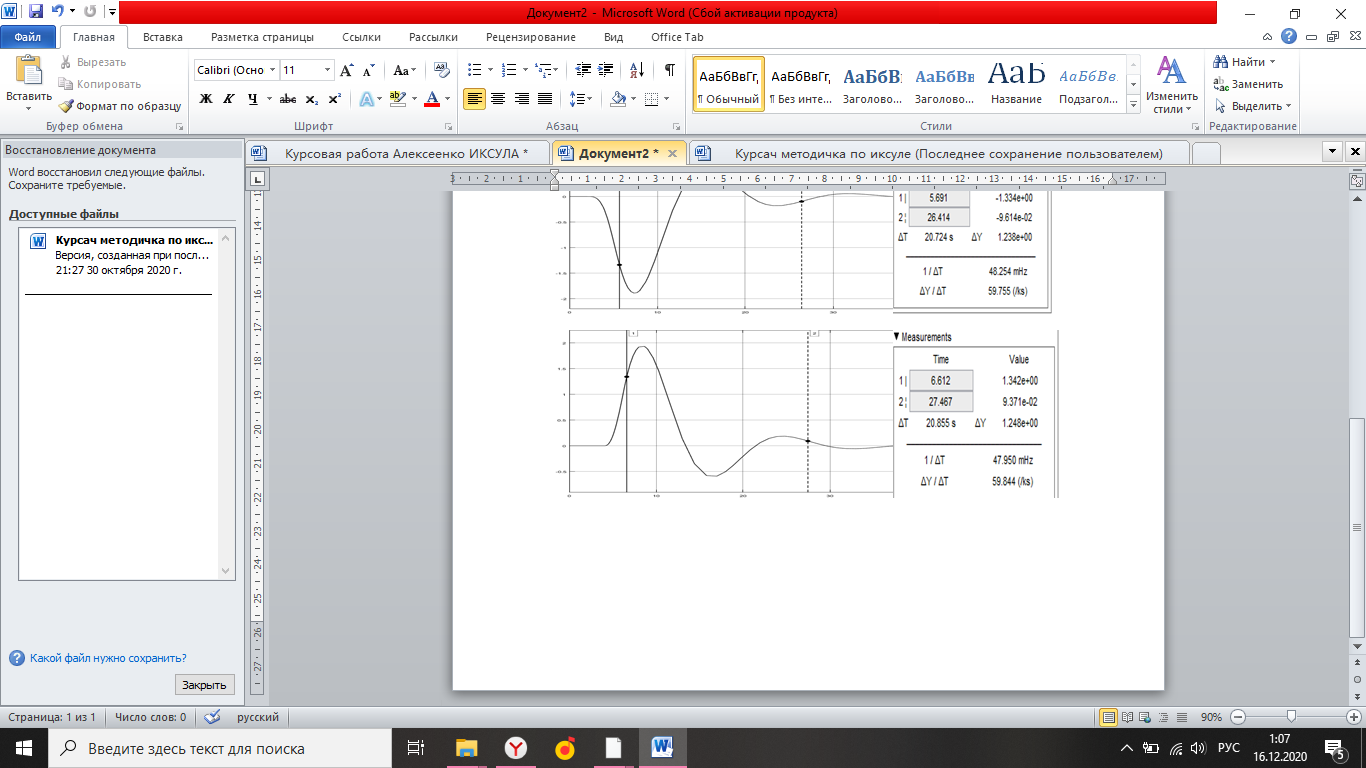 Рисунок 29- Результат моделирования при начальном сигнале «дача». tсраб= 6.612c; tзат= 27.467c. III. Результаты получившиеся при гармоническом сигнале на высоте 8000 метров расположены на рисунках 30-31. 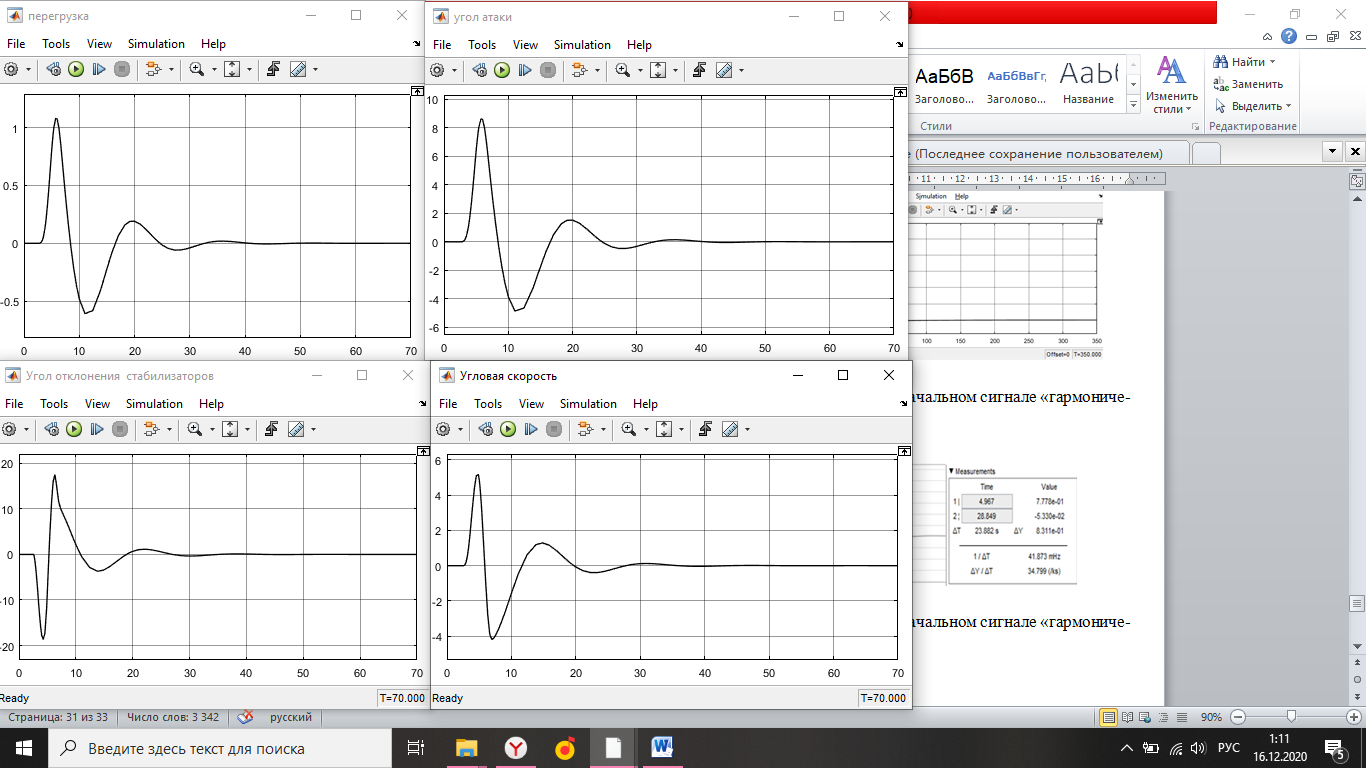 Рисунок 30- Результат моделирования при начальном сигнале «гармонический сигнал».  Рисунок 31- Результат моделирования при начальном сигнале «гармонический сигнал». tсраб= 6.967c; tзат= 28.849c. IV. Результаты получившиеся при сигнале «зубцы» на высоте 8000 метров расположены на рисунках 32-33. 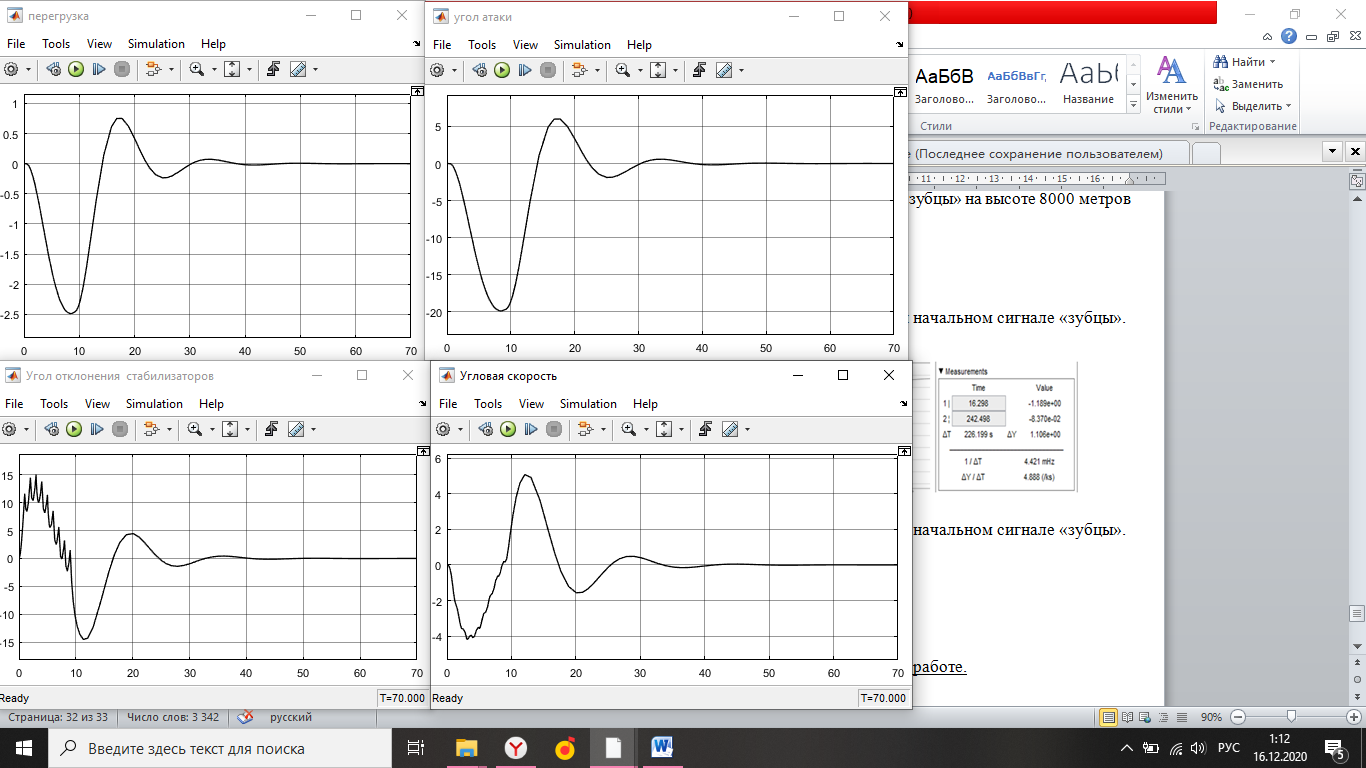 Рисунок 32- Результат моделирования при начальном сигнале «зубцы». 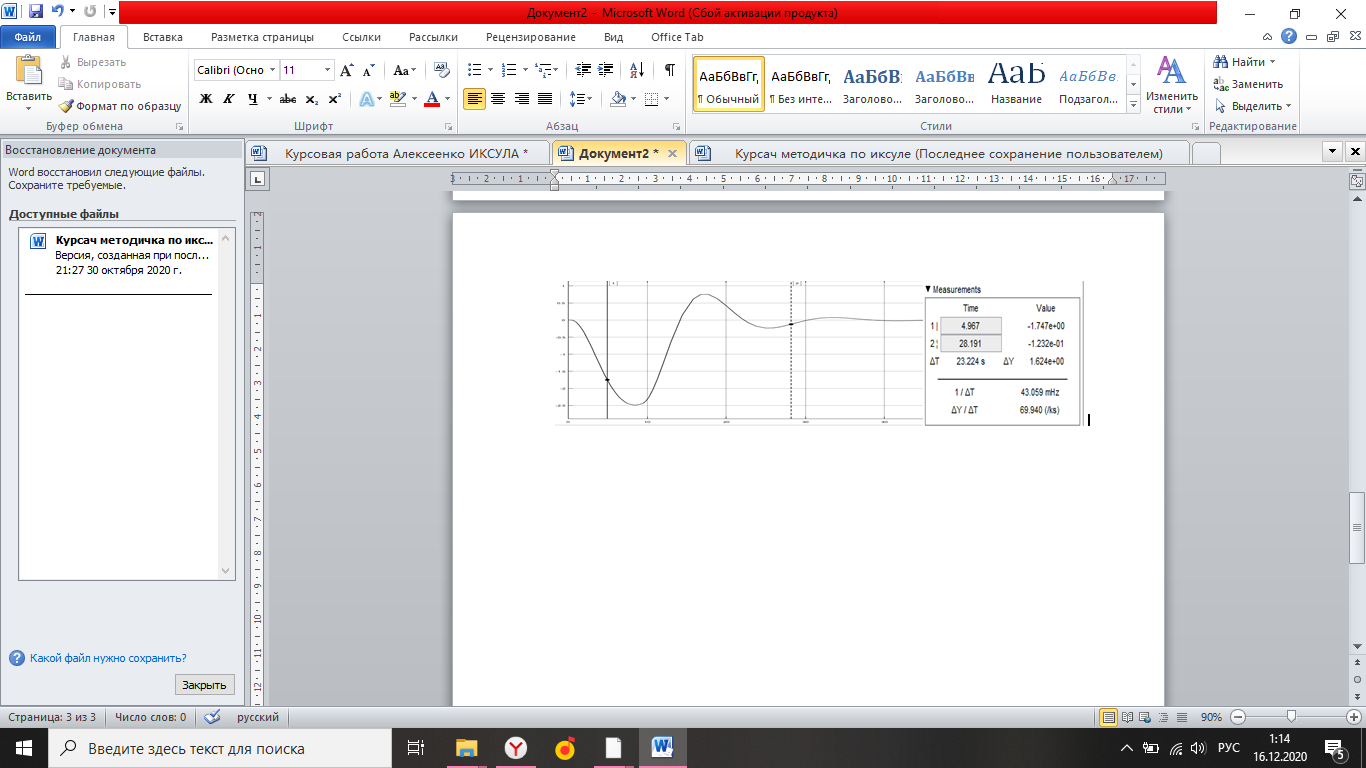 Рисунок 33- Результат моделирования при начальном сигнале «зубцы». tсраб= 4.967c; tзат= 28.191c. 4.Вывод по курсовой работе. При выполнение курсовой работы были разработаны модели систем автоматического управления. В задаче №3 были рассчитаны время затухания и срабатывания системы. |