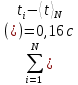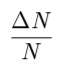Отчет по лабораторной работе 01 Исследование распределения случайной величины
 Скачать 294.53 Kb. Скачать 294.53 Kb.
|
 ГруппаL3116 К работе допущен _____________________ Студент Майорова Олеся Евгеньевна Работа выполнена __________________ Преподаватель Боярский Кирилл Кириллович Отчет принят Рабочий протокол и отчет по лабораторной работе № 1.01  Исследование распределения случайной величины.  Цель работы. Исследовать распределение случайной величины путём проведения многократного измерения определенного интервала времени (в частности, 5 секунд) и дальнейшей обработки данных. Задачи, решаемые при выполнении работы. Провести значительное количество измерений определенного интервала времени. Построить гистограмму распределения результатов измерения. Вычислить среднее значение и дисперсию полученной выборки. Сравнить гистограмму с графиком функции Гаусса с такими же, как и у экспериментального распределения средним значением и дисперсией. Объект исследования. Промежуток времени длиной в 5 секунд. Метод экспериментального исследования. Неоднократное измерение случайной величины. Измерительные приборы.
Схема установки (перечень схем, которые составляют Приложение 1).   Результаты прямых измерений и их обработки (таблицы, примеры расчетов). Таблица 1: Результаты прямых измерений
Найдем среднее арифметическое всех 50 измерений и занесем его в «подвал» Табл.1. 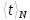 = 5,12 с = 5,12 сВычислим все значения 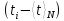 и занесем их в Табл. 1 в третий столбец. и занесем их в Табл. 1 в третий столбец.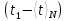 = 5,00 – 5,12 = - 0,12 (с) = 5,00 – 5,12 = - 0,12 (с)Вычислим по данной формуле значение и занесем его в «подвал» Табл. 1. 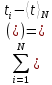 - 0,12 + 0,16 – 0,37 – 0,31 – 0,05 + … + 0,07 = 0,16 (с) - 0,12 + 0,16 – 0,37 – 0,31 – 0,05 + … + 0,07 = 0,16 (с)Вычислим все значения 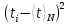 и занесем их в Табл. 1 в четвертый столбец. и занесем их в Табл. 1 в четвертый столбец.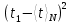 = (-0,12)2 = 0,0144 (c2) = (-0,12)2 = 0,0144 (c2)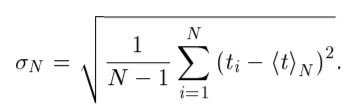 По данной формуле найдем средне квадратичное отклонение и занесем значение в «подвал» Табл. 1. 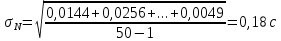 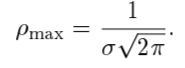 По данной формуле вычислим максимальное значение плотности распределения и занесем его в «подвал» Табл. 1. 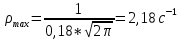 Расчет результатов косвенных измерений (таблицы, примеры расчетов). Построение гистограммы Найдем наименьший результат измерений. tmin = 4,65 с Найдем наибольший результат измерений. tmax = 5,66 c Возьмем m = 7, то есть разобьем промежуток 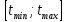 на 7 равных интервалов Δt=0,15 c. на 7 равных интервалов Δt=0,15 c.Занесем границы интервалов в первый столбец Табл. 2. Подсчитаем число результатов измерений ΔNi из Табл. 1, попавших в каждый из интервалов Δt, и занесем во второй столбец Табл. 2. Вычислим опытное значение плотности вероятности и занесем в третий столбец Табл. 2. 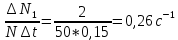 Найдем середины выбранных интервалов и занесем в четвертый столбец Табл. 2. 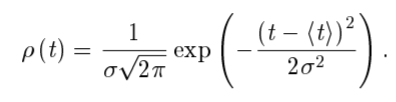 По данной формуле вычислим значение плотности распределения и занесем в пятый столбец Табл. 2. 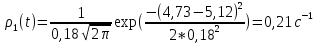 Таблица 2: Данные для построения гистограммы
Вычислим границы интервалов, заданные в первом столбце Табл. 3 и занесем их во второй столбец Табл. 3. По данным Табл. 1 подсчитаем количество ΔN измерений, попадающих в каждый из этих интервалов и отношение этого количества к общему числу измерений. Значения занесем в третий и четвертый столбцы Табл. 3. Таблица 3: Стандартные доверительные интервалы
Расчет погрешностей измерений (для прямых и косвенных измерений). Рассчитаем среднеквадратичное отклонение среднего значения по формуле: 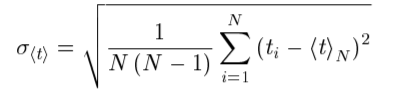 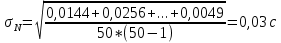 Найдем табличное значение коэффициента Стьюдента 𝑡𝛼,𝑁 для доверительной вероятности 𝛼 = 0,95: 𝑡𝛼,𝑁 = 2,04 Вычислим доверительный интервал для измеряемого в работе промежутка времени: Δt = 2,04 * 0,03 = 0,06 Графики (перечень графиков, которые составляют Приложение 2). Смотри Приложение 1 ( Гистограмма распределения результатов измерения ) Окончательные результаты. 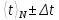 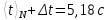 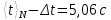 5,06 c ≤ t ≤ 5,18 c Выводы и анализ результатов работы. В данной работе я научилась исследовать закон распределение случайной величины. В качестве исследуемой случайной величины был выбран результат многократного измерения заданного промежутка времени. Для наглядности закономерности распределения значений изучаемой случайной величины все полученные данные я преобразовала и с помощью вычислений построила гистограмму распределения результатов измерения. Так же я сравнила ее с законом нормального распределения – функцией Гаусса, график которой построила в той же системе координат. Я заметила, что общий вид гистограммы и графика функции схожи, но максимальное значение несколько отличается, в связи с отсутствием учета погрешности, связанной с человеческой реакцией конкретного человека. Но в итоге можно утверждать, что исследование распределения данной случайной величины, в общем и целом, совпадает с нормальным распределением, описываемым функцией Гаусса. Также сравнение вероятности при условии реализации нормального распределения случайной величины (Таблица 3, столбец 5) и вычисленного мной приближенного значения вероятности (Таблица 3, столбец 4) наглядно показывает это (так как эти вероятности примерно равны). Замечания преподавателя (исправления, вызванные замечаниями преподавателя, также помещают в этот пункт). | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||