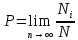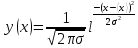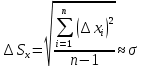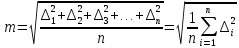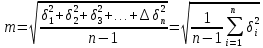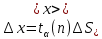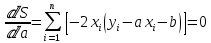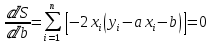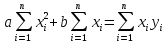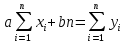информатика лаба 1. Фаткина Марина. Отчет по л.р. №1. Отчет по лабораторной работе 1 форматирование комплексного текстового документа по дисциплине Информатика
 Скачать 54.4 Kb. Скачать 54.4 Kb.
|
|
Санкт-Петербургский политехнический университет Петра Великого Институт машиностроения, материалов и транспорта Высшая школа машиностроения Отчет по лабораторной работе № 1 ФОРМАТИРОВАНИЕ КОМПЛЕКСНОГО ТЕКСТОВОГО ДОКУМЕНТА по дисциплине «Информатика»
Санкт-Петербург 2020 Цель работы – приобретение умений создания, редактирования и форматирования текстовых документов в соответствии с требованиями оформления, внедрения в документы различных объектов нетекстовой природы, а также использования средств автоматизации работы с текстами средствами текстового процессора Microsoft Word Задание Подготовить технический текст, состоящий из двух-трёх разделов, каждый из которых состоит из двух-трёх подразделов. Объём раздела две-три страницы. Текст должен содержать рисунки, таблицы, формулы. Отформатировать текст в соответствии с требованиями, представленными в таблицах 1, 2 и 3, а также с требованиями правил оформления текстовых документов. Таблица 1 — Параметры форматирования страницы
Таблица 2 — Параметры форматирования заголовков
Таблица 3 — Параметры форматирования абзацев и номеров страницы
ЭЛЕМЕНТАРНАЯ ОБРАБОТКА РЕЗУЛЬТАТОВ ФИЗИЧЕСКОГО ЭКСПЕРИМЕНТА Оглавление 1.Измерения 6 1.1.Погрешностииошибки в измерениях 6 1.2.Прямые измерения 7 1.3.Косвенныеизмерения 11 2.Представлениеэкспериментальныхрезультатов 12 2.1.Приближенныевычисления 14 1. Измерения 6 1.1. Погрешности и ошибки в измерениях 6 1.2. Прямые измерения 7 1.3. Косвенные измерения 11 2. Представление экспериментальных результатов 12 2.1. Приближенные вычисления 14 ИзмеренияПогрешностииошибки в измеренияхФизические величины являются вполне определенными, неслучайными (толщина пластины, разность температур, время между двумя событиями). Однако в процессе измерения из-за влияния различных случайных факторов (колебания почвы, перепады температуры и давления, изменение положения экспериментатора при отсчете по шкале и т.д.) результаты измерения – случайные величины. Основная задача при проведении измерений – указать наиболее точное значение измеряемой величины и ошибку (погрешность) измерения. Например, при измерении фокусного расстояния линзы f получено: f = (81 + 1) мм. Это означает, что наиболее точное значение фокусного расстояния равно 81 мм, а ошибка определения f– 1 мм. Величина погрешности используется при сравнительном анализе экспериментальных данных, позволяющем сделать обоснованный вывод. Например, необходимо установить, зависит ли сопротивление проволочной катушки от температуры. Измеренное сопротивление катушки оказалось равным 18,22 Ом при температуре 15С и 18,31 Ом при 25С. Следует ли придавать значение разнице этих величин? Если ошибка составляет 0,01 Ом, то разница значима, если ошибка равна 0,10 Ом, то – незначима. Для первого случая вывод: сопротивление катушки зависит от температуры. Во втором случае вывод: сопротивление катушки не зависит от температуры в пределах погрешности измерения. Ошибки (погрешности) измерения делятся на два типа: систематические и случайные. Систематическая ошибка – ошибка, которая остается постоянной на протяжении всей серии измерений. Систематические погрешности, как правило, обусловлены: 1) неисправностью измерительных приборов, 2) ошибочностью выбранного метода измерений, 3) упущениями со стороны наблюдателя. Их можно уменьшить, относясь критически к методам измерения и строго следя за исправным состоянием приборов. Если на измерительном инструменте не указана погрешность измерения, то за величину систематической ошибки принимается половина цены деления шкалы. Случайная ошибка – ошибка, которая изменяется произвольным образом от одного измерения к другому, в равной степени может быть как положительной, так и отрицательной. Случайные ошибки оцениваются методами математической статистики. Рассмотрим некоторые положения этой теории. ПрямыеизмеренияОбозначим истинное значение некоторой физической величины через x. Результаты n отдельных измерений – х, х,…, х (случайные величины). Тогда абсолютной ошибкой хii-го измерения называется разность: х= х – х. Абсолютные ошибки также являются случайными величинами. Огромное количество опытных фактов, накопленных в экспериментальной физике, позволяет установить два основополагающих предположения относительно абсолютных ошибок измерения: 1. При большом числе измерений случайные абсолютные ошибки одинаковой величины, но разного знака встречаются одинаково часто. 2. Большие (по абсолютной величине) погрешности встречаются реже, чем малые, т.е. вероятность появления погрешности уменьшается с ростом величины погрешности. Эти два предположения лежат в основе теории ошибок. При обработке результатов измерений в качестве наиболее точного значения величины х принимается среднее арифметическое из n измерений. Для оценки отклонения истинного значения х от среднего арифметического рассмотрим некоторые понятия теории вероятности. Случайная величина может быть дискретной (выпадение герба монеты или какой-либо грани кубика при подбрасывании), т.е. принимать ряд дискретных значений, или непрерывной (температура в помещении). Для дискретной величины: если в N опытах случайная величина появляется Ni раз, то вероятность Р появления этой величины вычисляется по следующей формуле
Пример. Если подбросить монету 10 раз, то пусть герб выпадет 3 раза и vi = 0,3 (vi= Ni/ N – относительная частота появления герба в опыте). Но если подбросить монету 105 раз, то vi будет очень близко к 0,5. Если подбросить 1010 раз, то vi будет еще ближе к 0,5. Таким образом, величина 0,5 – вероятность появления герба в опыте. Понятие вероятности справедливо для случайных процессов. Мы не знаем, появится ли данное событие (выпадение герба) в опыте, но мы характеризуем появление этого события понятием вероятности и численным значением вероятности. Если случайная величина х – непрерывная, то ставится вопрос: какова вероятность того, что случайная величина окажется в опыте в определенном бесконечно малом интервале dx около некоторого значения хi. Эта вероятность пропорциональна ширине интервала dx и зависит от значения xi, т.е. dP(x) = y(x)dx. За вероятность появления случайной величины х в интервале dx около значения xidP(xi) = y(xi) dx принимают относительную частоту появлений этой величины в интервале dx около значения xi, когда число измерений стремится к бесконечности. Главную роль в описании случайной величины, распределенной непрерывно, играет функция y(x), которая называется функцией распределения вероятностей. В математической статистике показано, что при выполнении предположений 1 и 2 функция распределения имеет вид (на рис.1 представлен график этой функции):
где 2 – дисперсия распределения. Распределение случайной величины такого типа называется нормальным распределением, или распределением Гаусса. Дисперсия показывает, насколько широко разбросаны значения случайной величины относительно среднего значения, что видно на рис. 1. Р 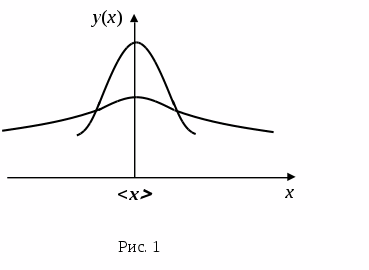 ис. 1 – график значений случайной величины относительно среднего значения Из теории математической статистики следует, что при n измерениях наиболее точную оценку дисперсии дает следующее выражение:
Величина Sx называется среднеквадратичной погрешностью отдельного измерения. Чтобы усилить влияние более крупных погрешностей на результат оценки точности ряда измерений, пользуются среднеквадратической погрешностью (СКП). Если известно истинное значение измеряемой величины, а систематическая погрешность пренебрежимо мала, то средняя квадратическая погрешность (m) отдельного результата равноточных измерений определяется по формуле Гаусса:
где Δi – истинная погрешность. В геодезической практике истинное значение измеряемой величины в большинстве случаев заранее неизвестно. Тогда среднюю квадратическую погрешность отдельного результата измерений вычисляют по вероятнейшим погрешностям (δ) отдельных результатов измерений; по формуле Бесселя:
Характеристикой того, как сильно среднее арифметическое значение отличается от истинного, служит доверительный интервал, для которого известно, с какой вероятностью истинное значение может находиться внутри этого интервала. Величина этой вероятности выбирается экспериментатором и называется надежностью. При выполнении лабораторных работ рекомендуется надежность , равная 0,95. Величина доверительного интервала х с заданной надежностью находится по данной формуле:
где t(n) – коэффициент Стьюдента, который можно найти в таблице для n измерений и надежности . . КосвенныеизмеренияКосвенные измерения основываются на использовании некоторых математических зависимостей между искомыми и непосредственно измеряемыми величинами. Например, нахождение объёма тела по его линейным размерам, нахождение плотности тела по измеренным массе и объёму, расчёт сопротивления про-водника по показаниям вольтметра и амперметра. Качество измерений определяется их точностью. При прямых измерениях точность опытов устанавливается из анализа точности метода и прибора, а также из повторяемости результатов измерений. Точность косвенных измерений определяется погрешностью исходных прямых измерений и структурой соответствующей расчётной формулы. ПредставлениеэкспериментальныхрезультатовПолученные в опыте значения измеряемой величины заносятся, как правило, в таблицу либо представляются в виде графика. Представление результатов измерений в виде графиков необходимо для наглядности и определения ряда величин. Масштаб выбирается таким, чтобы, во-первых, экспериментальные точки не сливались, во-вторых, обозначался простыми числами (10, 100, 0,1 и т.д. единиц соответствовали 1 см), в-третьих, занимал размеры около страницы. По осям откладываются деления и указываются символы величин и их единицы измерения. Погрешности изображаются в виде отрезков длиной в доверительный интервал. На рис. 2 представлен график зависимости углового ускорения ε от момента внешних сил М маятника Обербека, полученный в лабораторной работе “Изучение динамики вращательного движения твердого тела”. 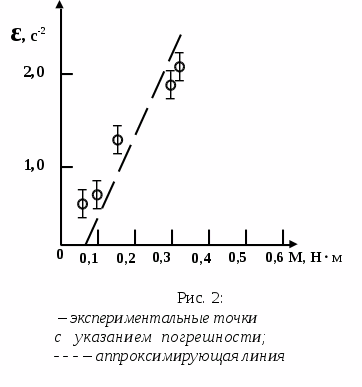 Рис. 2 – график зависимости углового ускорения ε от момента внешних сил М маятника Обербека. В физике широко распространена линейная зависимость между величинами, в том числе и между теми, которые изучаются экспериментально. В этом случае наилучший вид аппроксимирующей прямой может быть выбран методом наименьших квадратов. Рассмотрим этот метод. Пусть в эксперименте в n-измерениях получены пары значений (x1, y1), (x2, y2), … , (xn, yn), отвечающие зависимости y = ax + b, параметры a и b которой должны быть найдены. Предполагается, что с погрешностями определена лишь совокупность значений y. Тогда отклонение в каждом i-изменении значения аппроксимирующей прямой от экспериментально полученного yi составляет: yi – axi – b. Наилучшие значения a и b выбираются так, чтобы сумма квадратов ошибки была минимальной. Из условия минимума следует:
Для определения a и b получается система из двух уравнений
Отсюда вытекают формулы для искомых a и b
ПриближенныевычисленияРезультат измерений представляет собой приближенное число, точность которого определяется ошибкой. Пусть, например, в опыте с математическим маятником погрешность определения ускорения свободного падения равна 0,05 м/с2, а g равно 9,83 м/с2. Результат записывается в виде g = 9,83 0,05 м/с2. Очевидно, что вычислять результат опыта с точностью до тысячных долей не имеет смысла, так как ошибка составляет сотые доли, и тем более бесполезно указывать тысячные доли при записи результата. Полученное число (результат измерений) – приближенное, последняя цифра – сомнительная, а остальные верные. Так получается при любых измерениях. При записи окончательного результата оставляют только значащие цифры (верные и сомнительную цифры). Если приближенное число входит в расчетную формулу, в нем сохраняют одну “неверную” цифру. Далее пользуются правилами вычислений с приближенными числами и правилами округления. Вывод: благодаря данной работе мною были приобретены навыки создания, редактирования и форматирования текстовых документов в соответствии с требованиями оформления, научился добавлять в документы различные нетекстовые объекты (рисунки, таблицы, формулы) средствами текстового процессора Microsoft Word. |