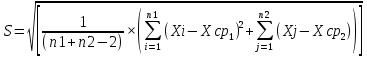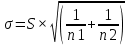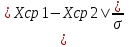Метрология и стандартизация. Контрольная работа по дисциплине Метрология, стандартизация и сертификация на тему Понятие погрешности измерений. Случайные и систематические погрешности, источники их появления
 Скачать 43.8 Kb. Скачать 43.8 Kb.
|
|
Министерство образования и науки РФ Казанский государственныЙ архитектурно-строительный университет Кафедра технологии, организации и механизации строительства Контрольная работа по дисциплине «Метрология, стандартизация и сертификация» на тему: «Понятие погрешности измерений. Случайные и систематические погрешности, источники их появления» (Вариант-64; Вопрос 2) выполнил студент группы 6 Пг01В Гордеев С.Ю. № зачетной книжки 0316564 Казань-2017 Качество средств и результатов измерений принято характеризовать, указывая их погрешности. Введение понятия "погрешность" требует определения и четкого разграничения трех понятий: истинного и действительного значений измеряемой физической величины и результата измерения. Истинное значение физической величины — это значение, идеальным образом отражающее свойство данного объекта как в количественном, так и в качественном отношении. Оно не зависит от средств нашего познания и является той абсолютной истиной, к которой мы стремимся, пытаясь выразить ее в виде числовых значений. На практике это абстрактное понятие приходится заменять понятием "действительное значение". Действительное значение физической величины (ФВ) — значение, найденное экспериментально и настолько приближающееся к истинному, что для данной цели оно может быть использовано вместо него. Результат измерения представляет собой приближенную оценку истинного значения величины, найденную путем измерения. Понятие "погрешность" — одно из центральных в метрологии, где используются понятия "погрешность результата измерения" и "погрешность средства измерения". Погрешность результата измерения — это разница между результатом измерения X и истинным (или действительным) значением Q измеряемой величины: Δ = Х-Q (1) Она указывает границы неопределенности значения измеряемой величины. Погрешность средства измерения — разность между показанием СИ и истинным (действительным) значением измеряемой ФВ. Она характеризует точность результатов измерений, проводимых данным средством. Эти два понятия во многом близки друг к другу и классифицируются по одинаковым признакам. По характеру проявления погрешности делятся на случайные, систематические, прогрессирующие и грубые (промахи). Заметим, что из приведенного выше определения погрешности никак не следует, что она должна состоять из каких-либо составляющих. Деление погрешности на составляющие было введено для удобства обработки результатов измерений исходя из характера их проявления, В процессе формирования метрологии было обнаружено, что погрешность не является постоянной величиной. Путем элементарного анализа установлено, что одна ее часть проявляется как постоянная величина, а другая — изменяется непредсказуемо. Эти части назвали систематической и случайной погрешностями. Разделение погрешности на систематическую, прогрессирующую и случайную составляющие представляет собой попытку описать различные участки частотного спектра этого широкополосного процесса: инфранизкочастотный, низкочастотный и высокочастотный. Случайная погрешность — составляющая погрешности измерения, изменяющаяся случайным образом (по знаку и значению) в серии повторных измерений одного и того же размера ФВ, проведенных с одинаковой тщательностью в одних и тех же условиях. В появлении таких погрешностей (рис. 1) не наблюдается какой-либо закономерности, они обнаруживаются при повторных измерениях одной и той же величины в виде некоторого разброса получаемых результатов. Случайные погрешности неизбежны, неустранимы и всегда присутствуют в результате измерения. Описание случайных погрешностей возможно только на основе теории случайных процессов и математической статистики. 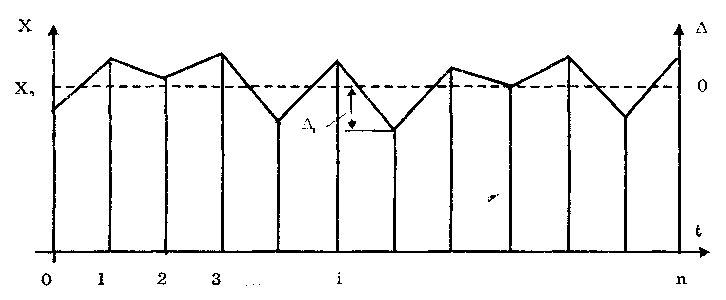 Рис. 1 . Изменение случайной погрешности от измерения к измерению В отличие от систематических случайные погрешности нельзя исключить из результатов измерений путем введения поправки, однако их можно существенно уменьшить путем увеличения числа наблюдений. Поэтому для получения результата, минимально отличающегося от истинного значения измеряемой величины, проводят многократные измерения требуемой величины с последующей математической обработкой экспериментальных данных. Большое значение имеет изучение случайной погрешности как функции номера наблюдения i или соответствующего ему момента времени t проведения измерений, т.е. i = (ti). Отдельные значения погрешности являются значениями функции A(t), следовательно, погрешность измерения есть случайная функция времени. При проведении многократных измерений получается одна реализация такой функции. Именно такая реализация показана на рис. 1. Повтор серии измерений даст нам другую реализацию этой функции, отличающуюся от первой, и т. д. Погрешность, соответствующая каждому i-му измерению, является сечением случайной функции (t). В каждом сечении данной функции можно найти среднее значение, вокруг которого группируются погрешности в различных реализациях. Если через полученные таким образом средние значения провести плавную кривую, то она будет характеризовать общую тенденцию изменения погрешности во времени. Систематическая погрешность — составляющая погрешности измерения, остающаяся постоянной или закономерно меняющаяся при повторных измерениях одной и той же ФВ. Постоянная и переменная систематические погрешности показаны на рис. 2. Их отличительный признак заключается в том, что они могут быть предсказаны, обнаружены и благодаря этому почти полностью устранены введением соответствующей поправки. Следует отметить, что в последнее время приведенное выше определение систематической погрешности подвергается обоснованной критике, особенно в связи с техническими измерениями. Весьма аргументированно предлагается считать систематическую погрешность специфической, "вырожденной" случайной величиной, обладающей некоторыми, но не всеми свойствами случайной величины, изучаемой в теории вероятностей и математической статистике. Ее свойства, которые необходимо учитывать при объединении составляющих погрешности, отражаются теми же характеристиками, что и свойства "настоящих" случайных величин: дисперсией (средним квадратическим отклонением) и коэффициентом взаимной корреляции [1]. В настоящее время, особенно после введения одного из основополагающих метрологических стандартов — ГОСТ 8.009-84 ТСИ. Нормируемые метрологические характеристики средств измерений", понятие "систематическая погрешность" несколько изменилось по отношению к определению, данному ГОСТ 16263-70 ТСИ. Метрология. Термины и определения". Систематическая погрешность считается специфической, "вырожденной" случайной величиной, обладающей некоторыми, но не всеми свойствами случайной величины, изучаемой в теории вероятностей и математической статистике. Свойства систематической погрешности, которые необходимо учитывать при объединении составляющих погрешности, отражаются такими же характеристиками, что и свойства "настоящих" случайных величин — дисперсией (СКО) и коэффициентом взаимной корреляции. 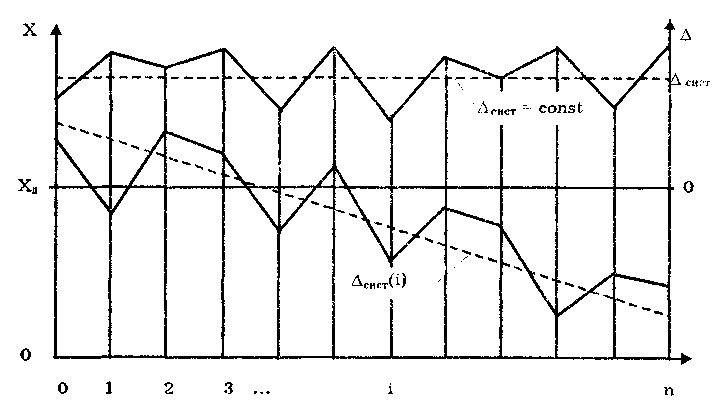 Рис. 2. Постоянная и переменная систематические погрешности Систематическая погрешность представляет собой определенную функцию влияющих факторов, состав которых зависит от физических, конструктивных и технологических особенностей СИ, условий их применения, а также индивидуальных качеств наблюдателя. В метрологической практике при оценке систематических погрешностей должно учитываться влияние следующих основных факторов: 1. Объект измерения. Перед измерением он должен быть достаточно хорошо изучен с целью корректного выбора его модели. Чем полнее модель соответствует исследуемому объекту, тем точнее могут быть получены результаты измерения. Например, кривизна земной поверхности может не учитываться при измерении площади сельскохозяйственных угодий, так как она не вносит ощутимой погрешности, однако при измерении площади океанов ею пренебрегать уже нельзя. 2. Субъект измерения. Его вклад в погрешность измерения необходимо уменьшать путем подбора операторов высокой квалификации и соблюдения требований эргономики при разработке СИ. 3. Метод и средство измерений. Чрезвычайно важен их правильный выбор, который производится на основе априорной информации об объекте измерения. Чем больше априорной информации, тем точнее может быть проведено измерение. Основной вклад в систематическую погрешность вносит, как правило, методическая погрешность. 4. Условия измерения. Обеспечение и стабилизация нормальных условий являются необходимыми требованиями для минимизации дополнительной погрешности, которая по своей природе, как правило, является систематической. Систематические погрешности принято классифицировать по двум признакам. По характеру изменения во времени они делятся на постоянные и переменные. Постоянными называются такие погрешности измерения, которые остаются неизменными в течение всей серии измерений. Например, погрешность от того, что неправильно установлен ноль стрелочного электроизмерительного прибора, погрешность от постоянного дополнительного веса на чашке весов и т.д. Переменными называются погрешности, изменяющиеся в процессе измерения. Они делятся на монотонно изменяющиеся, периодические и изменяющиеся по сложному закону. Если в процессе измерения систематическая погрешность монотонно возрастает или убывает, ее называют монотонно изменяющейся. Например, она имеет место при постепенном разряде батареи, питающей средство измерений. Периодической, называется погрешность, значение которой является периодической функцией времени. Примером может служить погрешность, обусловленная суточными колебаниями напряжения силовой питающей сети, температуры окружающей среды и др. Систематические погрешности могут изменяться и по более сложному закону, обусловленному какими-либо внешними причинами. По причинам возникновения погрешности делятся на методические, инструментальные и личные (субъективные). Инструментальная погрешность обусловлена погрешностью применяемого СИ. Иногда эту погрешность называют аппаратурной. Методическая погрешность измерения обусловлена: • отличием принятой модели объекта измерения от модели, адекватно описывающей его свойство, которое определяется путем измерения; • влиянием способов применения СИ. Это имеет место, например, при измерении напряжения вольтметром с конечным значением внутреннего сопротивления. В данном случае вольтметр шунтирует участок цепи, на котором измеряется напряжение, и оно оказывается меньше, чем было до присоединения вольтметра; • влиянием алгоритмов (формул), по которым производятся вычисления результатов измерений; • влиянием других факторов, не связанных со свойствами используемых средств измерения. Отличительной особенностью методических погрешностей является то, что они не могут быть указаны в нормативно-технической документации на используемое СИ, поскольку от него не зависят, а должны определяться оператором в каждом конкретном случае. В связи с этим оператор должен четко различать фактически измеряемую им величину и величину, подлежащую измерению. Субъективная (личная) погрешность измерения обусловлена погрешностью отсчета оператором показаний по шкалам СИ, диаграммам регистрирующих приборов. Они вызываются состоянием оператора, его положением во время работы, несовершенством органов чувств, эргономическими свойствами СИ. Характеристики личной погрешности определяют на основе нормированной номинальной цены деления шкалы измерительного прибора (или диаграммной бумаги регистрирующего прибора) с учетом способности "среднего оператора" к интерполяции в пределах деления шкалы [1]. Случайная (Δсл) и систематическая (Δc) составляющие погрешности измерения проявляются, как правило, одновременно. Общая погрешность при их независимости определяется их суммой Δ=Δсл+Δc, или через среднеквадратическое отклонение 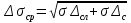 (2) (2)Значение случайной погрешности заранее неизвестно, оно возникает из-за множества неутонченных факторов. Для уменьшения случайной погрешности есть два пути: или повышать точность измерений (уменьшение 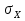 ), или увеличивать числа измерений (n). ), или увеличивать числа измерений (n). Если считать, что все возможности совершенствования техники измерений использованы, то остается только второй путь. При этом отметим, что уменьшать случайную составляющую погрешности целесообразно лишь до тех пор, пока общая погрешность измерений не будет полностью определяться систематической составляющей Δс. Если систематическая погрешность определяется классом точности средств измерения (Δси), то необходимо, чтобы доверительный интервал ±tp· 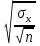 , где tp — коэффициент Стьюдента, был существенно меньше Δс. , где tp — коэффициент Стьюдента, был существенно меньше Δс.Обычно принимают 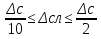 при доверительной вероятности Р = 0,95. В случае невозможности выполнения этого условия необходимо коренным образом изменить методику измерения. при доверительной вероятности Р = 0,95. В случае невозможности выполнения этого условия необходимо коренным образом изменить методику измерения. При сравнении случайных погрешностей с различными законами распределения использование показателей, которые сводят плотность распределения к одному или нескольким числам, обязательно. Такими числами могут быть среднеквадратическое отклонение, доверительный интервал (от Хср-Δсл до Хср+Δсл) и доверительная вероятность. Надежность самого среднеквадратического отклонения (σσ) определяется по формуле σσ= 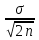 Принято считать, что если σσ≤0,25 σ, то оценка точности надежна. Это условие выполняется уже при n = 8. На практике важно уметь правильно сформулировать требования к точности измерений. Например, если за допустимую погрешность измерения принять Δ = 3 σ то, повышая требования к контролю, при сохранении технологии изготовления изделий увеличивается вероятность брака. Наиболее вероятная погрешность (Δв) отдельного измерения определяется по формуле Δв = 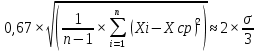 (3) (3)Таким образом, с увеличением n значение вероятной погрешности Л, быстро уменьшается, но лишь до n = 5. Следовательно, увеличение числа измерений на одном режиме больше 5 нецелесообразно, что соответствует условию получения надежных значений σσ. Число измерений определяют, используя одно из выражений: где n— число отбрасываемых экспериментальных результатов. 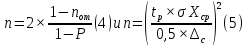 С учетом коэффициентов Стьюдента можно оценить относительную погрешность отдельного измерения: 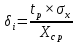 (6) (6)И его среднего значения: 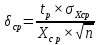 (7) (7)Считается, что систематические погрешности могут быть обнаружены и исключены. Однако в реальных условиях полностью исключить систематическую составляющую погрешности невозможно. Всегда остаются какие-то неисключенные факторы, которые нужно учитывать, и которые будут систематической погрешностью измерения. То есть, систематическая погрешность тоже случайна, и ее определение обусловлено лишь установившимися традициями обработки и представления результатов измерения. Необнаруженная систематическая составляющая погрешности опаснее случайной: если случайная составляющая вариацию (разброс) результатов, то систематическая — устойчиво их искажает (смещает). В любом случае отсутствие или незначительность (пренебрежение) систематической погрешности надо доказать. Действительно, если взять два ряда измерений одной и той же величины, то средние результаты этих рядов, как правило, будут различны. Это расхождение может быть определено случайной или систематической составляющей. Последовательность выявления характера погрешности
Таким образом, для характеристики случайной погрешности надо обязательно задать два числа: величину самой погрешности (или доверительный интервал от Хср-Δсл до Хср+Δсл) и доверительную вероятность. [2]. Прогрессирующая (дрейфовая) погрешность — это непредсказуемая погрешность, медленно меняющаяся во времени. Впервые это понятие было введено в монографии М.Ф. Маликова "Основы метрологии", изданной в 1949 г. Отличительные особенности прогрессирующих погрешностей: • они могут быть скорректированы поправками только в данный момент времени, а далее вновь непредсказуемо изменяются; • изменения прогрессирующих погрешностей во времени — нестационарный случайный процесс, и поэтому в рамках хорошо разработанной теории стационарных случайных процессов они могут быть описаны лишь с известными оговорками. Прогрессирующая погрешность — это понятие, специфичное для нестационарного случайного процесса изменения погрешности во времени, оно не может быть сведено к понятиям случайной и систематической погрешностей. Последние характерны лишь для стационарных случайных процессов. Прогрессирующая погрешность может возникнуть вследствие как непостоянства во времени текущего математического ожидания нестационарного случайного процесса, так и изменения во времени его дисперсии или формы закона распределения. Понятие прогрессирующей погрешности широко используется при исследовании динамики погрешностей СИ и метрологической надежности последних. Грубая погрешность (промах) — это случайная погрешность результата отдельного наблюдения, входящего в ряд измерений, которая для данных условий резко отличается от остальных результатов этого ряда. Они, как правило, возникают из-за ошибок или неправильных действий оператора (его психофизиологического состояния, неверного отсчета, ошибок в записях или вычислениях, неправильного включения приборов или сбоев в их работе и др.). Возможной причиной возникновения промахов также могут быть кратковременные резкие изменения условий проведения измерений. Если промахи обнаруживаются в процессе измерений, то результаты, их содержащие, отбрасывают. Однако чаще всего промахи выявляют только при окончательной обработке результатов измерений с помощью специальных критериев [1]. Список использованных источников:
|