Отчет по лабораторной работе №1 исследование электростатического. Отчет по лабораторной работе 1 исследование электростатического поля методом моделирования в проводящей среде
 Скачать 0.55 Mb.
|
ОТЧЕТПО ЛАБОРАТОРНОЙ РАБОТЕ № 1«ИССЛЕДОВАНИЕ ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ МЕТОДОМ МОДЕЛИРОВАНИЯ В ПРОВОДЯЩЕЙ СРЕДЕ » Цель работы: исследование конфигурации электростатического поля; построение эквипотенциалей и линий напряженности для заданной формы электродов; приобретение навыков в применении теоремы Гаусса на примере определения электроемкости системы по экспериментально найденному распределению поля. Приборы и принадлежности: пантограф с зондом, измерительная схема, лист чистой бумаги. Общие сведения. Электростатическое поле определено, если в каждой точке пространства известны величина и направление вектора напряженности Е или значение потенциала  этого поля. В первом случае мы имеем дело с векторным представлением поля, во втором - со скалярным. Между этими представлениями существует связь, выражающаяся соотношением: (1.1)В диэлектриках электростатическое поле характеризуется вектором электрического смещения (электрической индукции)  , который удовлетворяет теореме Гаусса: где Q - суммарный свободный заряд, заключенный в объеме, ограниченном поверхностью S . Для однородного диэлектрика  (1.2)Электрическое поле потенциально, т.е. работа электрических сил по перемещению заряда не зависит от формы траектории; работа по замкнутому пути равна нулю. Математически это соответствует тому, что циркуляция вектора напряженности электростатического поля также равна нулю:  (1.3)Соотношения (1.2) и (1.3) дают исчерпывающее описание свойств электростатического поля. В данной работе рассматриваются две типичные задачи электростатики: определение и Е поля заданного распределения зарядов и вычисление емкости системы проводников.Во многих случаях прямой расчет электростатического поля заменяют его моделированием. Наиболее удобной моделью является электрическое поле в проводящей среде. Если электроды, к которым приложена разность потенциалов, помещены в проводящую среду, то в межэлектродном пространстве возникает электрический ток, плотность которого  связана с напряженностью Е. электрического поля, установившегося в среде, законом Ома: , (1.4)где  - удельная проводимость среды. Таким образом, линии тока (траектории движения носителей тока в проводящей среде) совпадают с линиями напряженности электрического поля. В отсутствии сторонних сил линии тока будут перпендикулярны поверхностям равного потенциала, следовательно, соотношение (1.1) справедливо и для электрического поля в проводящей среде.Продолжая аналогию, можно для электрического поля в проводящей среде найти соотношение, подобное теореме Гаусса (1.2). Если не рассматривать перенос заряда сторонними силами, то из очевидного выражения:  ,где  - ток, текущий от электрода; S - замкнутая поверхность, охватывающая электрод, придем к соотношению: ,подобному (1.2). Потенциальный характер электрического поля в проводящей среде иллюстрируется соотношением:  ,которое легко доказать, вычисляя, например, циркуляцию вектора  по замкнутому контуру  , расположенному на эквипотенциальной поверхности. Учитывая (1.4), получим подобное (1.3) выражение .На основании подобия свойств векторов  и  можно сделать вывод о возможности моделирования электростатического поля электрическим полем в проводящей среде, если соблюдается подобие формы и расположения электродов в пространстве. Масштабные коэффициенты проводящей модели вычисляются из сопоставления тока и заряда Q, а также удельной проводимости и абсолютной диэлектрической проницаемости  модели и электростатического аналога с учетом их размеров.Электрическое поле проводящей модели определяют, измеряя распределение потенциалов в ней, после чего, используя (1.1), рассчитывают поле вектора напряженности. Электроемкость системы электродов можно определить прямым измерением сопротивления проводящей среды между электродами. Можно показать,  ,где R - сопротивление проводящий среды. Можно также вычислить емкость электродов с использованием теоремы Гаусса, учитывая, что 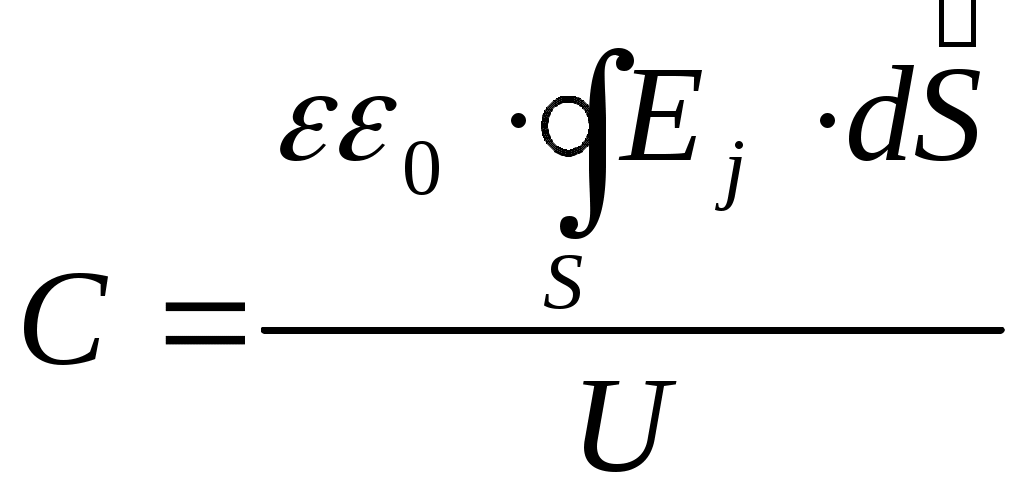 ( - разность потенциалов между электродами). Получаем для определения емкости , (1.5)где поток вектора  вычисляется по поверхности, охватывающей электрод моделируемой системы; U - напряжение между электродами модели;  - проницаемость моделируемого диэлектрика. Соотношение (1.5) удобно тем, что в качестве поверхности S берется определенная на модели эквипотенциальная поверхность.Методика измерений. В настоящей работе моделируется плоское поле, т.е. такое, потенциал и напряженность которого зависят от двух координат. Плоским являются, например, поле двухпроводной линии или же поле, образованное заряженными плоскостью и проводником. Для описания таких полей достаточно найти распределение в плоскости, перпендикулярной к электродам, тогда полная картина поля образуется смещением полученного сечения вдоль оси, перпендикулярной к этому сечению. В экспериментальной установке воспроизводится сечение системы электродов, формирующих один из возможных вариантов плоского поля. В качестве проводящей среды используется проводящая бумага. Электрическая схема измерительной установки приведена на рис.1.1. Схема представляет собой мост постоянного тока, одно плечо которого образовано сопротивлениями участков аb и bс потенциометра R1 между его концевыми и подвижным контактами; другое плечо - сопротивления участков проводящей бумаги (1) между зондом (2) и электродами. 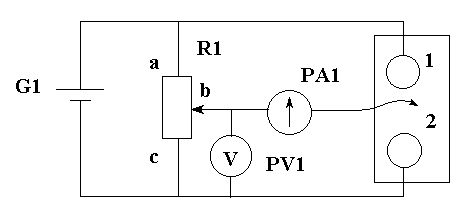 Рис. 1.1. В диагональ моста включен микроамперметр PA1. Ток в диагонали моста равен нулю, когда падение напряжения на участке bc резистора R1. 1 равно разности потенциалов между зондом и нижним по схеме электродом. Потенциал одного электрода принимается равным нулю. Перемещая зонд по листу проводящей бумаги, можно исследовать распределение потенциала на поверхности листа. С помощью пантографа координаты зонда переносятся на чистый лист бумаги, закрепленный под вторым плечом пантографа. Если отмечать точки, соответствующие одному и тому же падению напряжения на участке bc резистора R1 , а затем менять его с заданным шагом  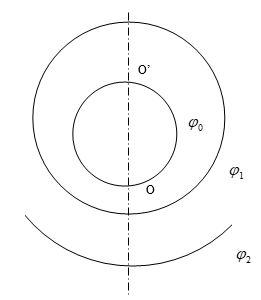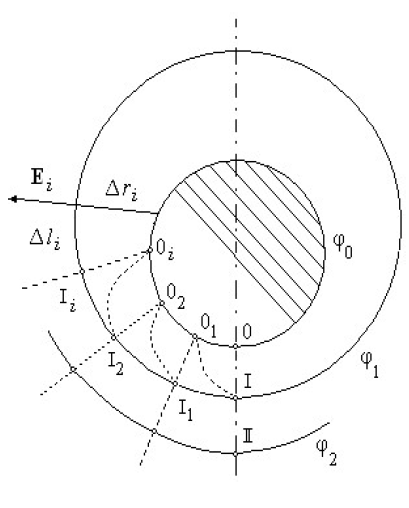, то в результате получится карта эквипотенциалей с шагом . Примерный вид карты поля около одного из электродов моделируемой системы приведен на рис. 1.2.    Рис. 1.2. Для построения линий напряженности (силовых линий) используется следующий прием. Вначале проводят линию OO' (рис.1.2), соединяющую электроды, так, чтобы она совпадала с осью симметрии поля. От точки О вдоль контура электрода откладывают отрезок  , равный кратчайшему расстоянию O1 от точки O до эквипотенциали  , и получают точку  . Затем от точки откладывают отрезок  , равный кратчайшему расстоянию  от точки до эквипотенциали  и получают точку  и т.д. Последней точкой на контуре электрода будет та, от, которой откладывается отрезок, накрывающий точку O', диаметрально противоположную точке О. Аналогичное построение проводят от точки О в другую сторону. Разделив указанным образом ближайшую к электроду эквипотенциаль, через полученные точки  … проводят перпендикулярные к ней отрезки до пересечения со следующей эквипотенциалью. Когда будут разделены все эквипотенциали карты поля, полученные точки следует соединить плавными линиями, соблюдая их ортогональность эквипотенциальным линиям в точках пересечения.Для вычисления емкости, приходящейся на единицу длины рассматриваемых электродов, необходимо с помощью формулы (1.2) рассчитать поток вектора напряженности через поверхность, охватывающую единицу длины электрода. Для этого следует представить, что ближайшая к электроду замкнутая эквипотенциаль является цилиндром, образующая которого перпендикулярна плоскости листа. Полагая напряженность поля в пределах каждого из отрезков  примерно одинаковой, можно вычислить поток  вектора  . через  -ый элемент поверхности цилиндра: ,где  - высота цилиндра, - длина отрезка эквипотенциали, измеряемая по карте поля определяется по формуле , (1.6)  расстояние между соответствующими отрезками электроде и ближайшей к нему эквипотенциали; ( ) - разность потенциалов между электродом и ближайшей к нему эквипотенциалью. Заряд, заключенный внутри замкнутой поверхности цилиндра, вычисляется по теореме Гаусса суммированием потоков через все элементы поверхности цилиндра: . Последнее соотношение используется для нахождения емкости единицы длины (погонной емкости) моделируемой системы:  . (1.7)Указания по выполнению наблюдений и обработке результатов 1. Закрепить на правой плате пантографа карту (лист чистой бумаги, равный по размеру проводящему листу). С помощью пантографа перенести на карту очертания электродов. Собрать и включить измерительную установку. 2. Измерить разность потенциалов , между электродами. Для этого надо установить зонд на один из электродов и, вращая ручку потенциометра  , добиться исчезновения тока через микроамперметр. Показания вольтметра PV1 будут соответствовать потенциалу электрода. Аналогичную операцию проделать для другого электрода. 3. Сместить зонд на небольшое (5-7 мм) расстояние от электрода. Потенциометром установить нуль микроамперметра, при этом вольтметр покажет значение в данной точке поля. Перемещая зонд вокруг электрода с сохранением нулевых показаний микроамперметра, перенести на карту 10-12 точек первой эквипотенциали (данная эквипотенциаль должна быть замкнутой). Соединив полученные точки плавной линией, изобразить эквипотенциаль на карте, рядом записать значение потенциала. 4. Вращая ручку потенциометра R1 , изменить показания вольтметра на (величина указана, на панели установки) и, перемещая зонд по поверхности бумаги, найти и перенести на карту положение 10-12 точек, для которых сохраняются нулевые показания микроамперметра PA1. Подобным образом с шагом построить семейство эквипотенциалей, заполняющих всю поверхность листа.5. Построить на полученной карте силовые линии электрического поля. Вычислить по формуле (1.6) и построить (масштаб указать на карте) вектор напряженности в точке А. 6. Вычислить по формуле (1.7) емкость моделируемой системы, (значение указано на панели установки).7. Вывести аналитическое выражение для емкости моделируемой системы, рассчитать теоретическое значение емкости, используя данные измерений геометрических размеров моделируемой системы, сравнить полученное значение с вычисленным в п.6. 8. Рассчитать значение плотности энергии электрического поля в пределах каждого из отрезков первой эквипотенциали (  ).Обработка результатов наблюдений1.  По карте поля определим:  2.  3.  4.  5. Определение напряженности поля в точке А По карте поля определяем расстояние от центра цилиндрического зонда до точки А(  ).Для случая  п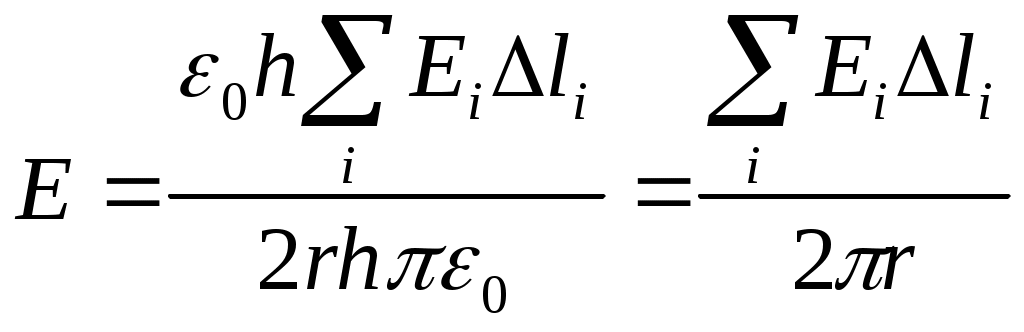рименим теорему Гаусса-Остроградского: , т.к. вектор нормали к боковой поверхности цилиндра совпадает с направлением вектора напряженности, то  , тогда, т.к. известно, что  и получим  , подставляя числовые значения, получим  .6. Определение напряженности поля в точке А2 (вариант Бродкина Михаила). По карте поля определяем расстояние от центра цилиндрического зонда до точки А2 (  ).Для случая п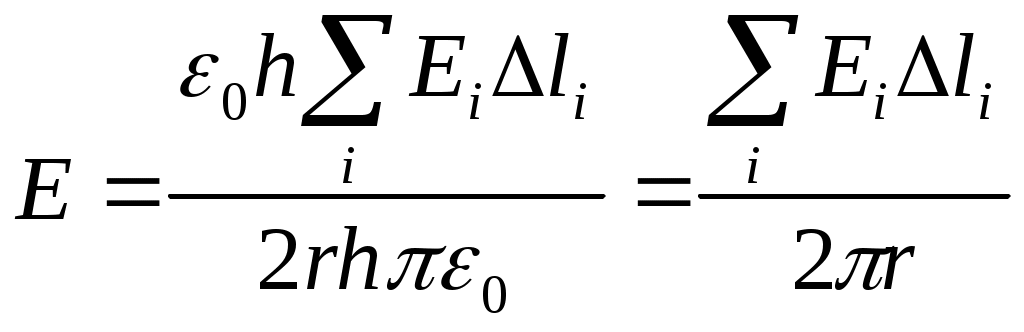рименим теорему Гаусса-Остроградского: , т.к. вектор нормали к боковой поверхности цилиндра совпадает с направлением вектора напряженности, то , тогда, т.к. известно, что и получим , подставляя числовые значения, получим  .Вывод: в ходе лабораторной работы мы исследовали конфигурации электростатического поля; построили эквипотенциали и линии напряженности для заданной формы электродов; применили теорему Гаусса на примере определения электроемкости системы по экспериментально найденному распределению поля  , вывели формулу для нахождения напряженности поля в любой точке и вычислили напряженность в А , в А2 . |