Отчет. Отчет по лабораторной работе 1 Классификация по дисциплине Машинное обучение

• Название: Отчет по лабораторной работе 1 Классификация по дисциплине Машинное обучение
• Дата: 29.04.2022
• Размер: 1.97 Mb.
• Имя файла: Отчет.docx
• Тип: Отчет; #503844

Санкт-Петербургский политехнический университет Петра Великого

Институт компьютерных наук и технологий

Высшая школа программной инженерии

Отчет по лабораторной работе №1

«Классификация»

по дисциплине «Машинное обучение»

Выполнил

студент гр. 3530904/90102 Дергунов Н. С.


Руководитель

старший преподаватель ВШПИ Селин И. А.

Оглавление

Задачи 3

Исследование влияния объема обучающей выборки и количества тестовых данных на точность классификации 6

Оценка качества классификации с помощью различных методов 9

Классификатор k ближайших соседей. 12

Метод опорных векторов 13

Классификатор на основе дерева решений. 22

Классификация для банка 26

Приложения 27

Приложение 1.1 27

Приложение 1.2 28

Приложение 2 29

Приложение 3 31

Приложение 4.1 32

Приложение 4.2 33

Приложение 4.3 35

Приложение 4.4 37

Приложение 5.1 39

Приложение 5.2 41

Приложение 6 43

Задачи

1. 
   Исследуйте, как объем обучающей выборки и количество тестовых данных, влияет на точность классификации в датасетах про крестики-нолики (tic_tac_toe.txt) и о спаме e-mail сообщений (spam.csv) с помощью наивного Байесовского классификатора. Постройте графики зависимостей точности на обучающей и тестовой выборках в зависимости от их соотношения.
   
2. 
   Сгенерируйте 100 точек с двумя признаками X1 и X2 в соответствии с нормальным распределением так, что одна и вторая часть точек (класс -1 и класс 1) имеют параметры: мат. ожидание X1, мат. ожидание X2, среднеквадратические отклонения для обеих переменных, соответствующие вашему варианту (указан в таблице). Построить диаграммы, иллюстрирующие данные. Построить Байесовский классификатор и оценить качество классификации с помощью различных методов (точность, матрица ошибок, ROС и PR-кривые). Является ли построенный классификатор «хорошим»?
   
3. 
   Постройте классификатор на основе метода k ближайших соседей для обучающего множества Glass (glass.csv). Посмотрите заголовки признаков и классов. Перед построением классификатора необходимо также удалить первый признак Id number, который не несет никакой информационной нагрузки.
   
   1. 
      Постройте графики зависимости ошибки классификации от количества ближайших соседей.
      
   2. 
      Определите подходящие метрики расстояния и исследуйте, как тип метрики расстояния влияет на точность классификации.
      
   3. 
      Определите, к какому типу стекла относится экземпляр с характеристиками:
      RI =1.516 Na =11.7 Mg =1.01 Al =1.19 Si =72.59 K=0.43 Ca =11.44 Ba =0.02 Fe =0.1
      
4. 
   Постройте классификаторы на основе метода опорных векторов для наборов данных из файлов svmdataN.txt и svmdataNtest.txt, где N – индекс задания:
   
   1. 
      Постройте алгоритм метода опорных векторов с линейным ядром. Визуализируйте разбиение пространства признаков на области с помощью полученной модели (пример визуализации). Выведите количество полученных опорных векторов, а также матрицу ошибок классификации на обучающей и тестовой выборках.
      
   2. 
      Постройте алгоритм метода опорных векторов с линейным ядром. Добейтесь нулевой ошибки сначала на обучающей выборке, а затем на тестовой, путем изменения штрафного параметра. Выберите оптимальное значение данного параметра и объясните свой выбор. Всегда ли нужно добиваться минимизации ошибки на обучающей выборке?
      
   3. 
      Постройте алгоритм метода опорных векторов, используя различные ядра (линейное, полиномиальное степеней 1-5, сигмоидальная функция, гауссово). Визуализируйте разбиение пространства признаков на области с помощью полученных моделей. Сделайте выводы.
      
   4. 
      Постройте алгоритм метода опорных векторов, используя различные ядра (полиномиальное степеней 1-5, сигмоидальная функция, гауссово). Визуализируйте разбиение пространства признаков на области с помощью полученных моделей. Сделайте выводы.
      
   5. 
      Постройте алгоритм метода опорных векторов, используя различные ядра (полиномиальное степеней 1-5, сигмоидальная функция, гауссово). Изменяя значение параметра ядра (гамма), продемонстрируйте эффект переобучения, выполните при этом визуализацию разбиения пространства признаков на области.
      
5. 
   Постройте классификаторы для различных данных на основе деревьев решений:
   
   1. 
      Загрузите набор данных Glass из файла glass.csv.
      Постройте дерево классификации для модели, предсказывающей тип (Type) по остальным признакам. Визуализируйте результирующее дерево решения. Дайте интерпретацию полученным результатам. Является ли построенное дерево избыточным? Исследуйте зависимость точности классификации от критерия расщепления, максимальной глубины дерева и других параметров по вашему усмотрению.
      
   2. 
      Загрузите набор данных spam7 из файла spam7.csv. Постройте оптимальное, по вашему мнению, дерево классификации для параметра yesno. Объясните, как был осуществлён подбор параметров. Визуализируйте результирующее дерево решения. Определите наиболее влияющие признаки. Оцените качество классификации.
      
6. 
   Загрузите набор данных из файла bank_scoring_train.csv. Это набор финансовых данных, характеризующий физических лиц. Целевым столбцом является «SeriousDlqin2yrs», означающий, ухудшится ли финансовая ситуация у клиента. Постройте систему по принятию решения о выдаче или невыдаче кредита физическому лицу. Сделайте как минимум 2 варианта системы на основе различных классификаторов. Подберите подходящую метрику качества работы системы исходя из специфики задачи и определите, принятие решения какой системой сработало лучше на bank_scoring_test.csv.
   

Исследование влияния объема обучающей выборки и количества тестовых данных на точность классификации

При построении Байесовского классификатора для игры крестик нолики было использовано различная доля тренировочных данных от 0.02 до 0.98, результаты приведены на двух графиках





Если отбросить слишком малые и большие доли тестовой выборки результаты, точность результатов не зависит от доли обучающих и тестовых данных

Код программы в приложении 1.1

Для датасета spam.csv, были получены подобные результаты, код программы в приложении 1.2.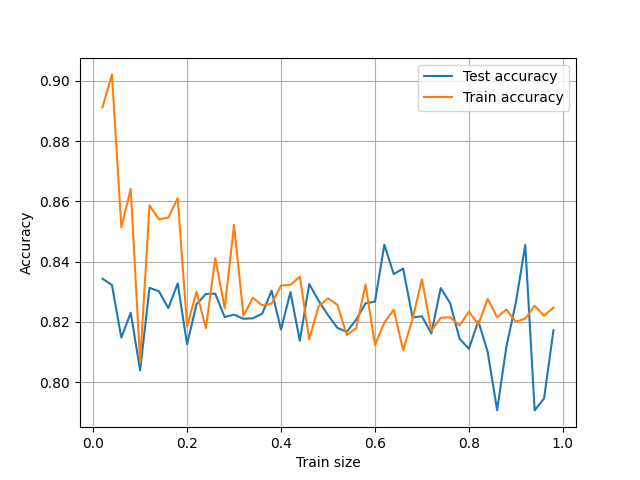

Оценка качества классификации с помощью различных методов

Выполнен 6 вариант

Было сгенерировано с 60 точек класса -1, признак X1 имел математическое ожидание 15, среднеквадратическое отклонение 3, признак X2 имел математическое ожидание 9 с тем же среднеквадратическим отклонением. Так же сгенерировано 40 точек класса +1, признак X1 имел математическое ожидание 15, дисперсию 5, признак X2 имел математическое ожидание 8 с той же дисперсией. Для обучения было выделено 80 точек 20 для теста.



Точность получилась 0.65

Таблица ошибок
	Класс -1	Класс 1
Класс -1	8	2
Класс 1	5	5

На пердставленных данных результатах мы получили приемлемые результаты, так как наш предсказател работает лучше случайного, но при перезапуске программы бывали и случаи при которых выдывался ответ хуже, PR кривая лежала ниже графика случайного распределоения, поэтому считаю что Байесовский классификатор в данных условиях работает плохо. Код в приложении 2.

Классификатор k ближайших соседей.

Датасет был разбит на 0.75 и 0.25 для тренировочных и тестовых данных соответственно



Как видно лучший результат достигается при 1 соседе.

Метрики расстояния	Точность
Евклидова	0.6851851851851852
Манхэттенская	0.7037037037037037
Чебышева	0.6111111111111112
Минковского	0.6851851851851852

Лучший результат продемонстрировала Манхэттенская метрика расстояния, худший Чебышева.

Экземпляр с характеристиками RI =1.516 Na =11.7 Mg =1.01 Al =1.19 Si =72.59 K=0.43 Ca =11.44 Ba =0.02 Fe =0.1 принадлежит 5 типу стекла.

Код представлен в приложении 3.

Метод опорных векторов

Был построен алгоритм на основе метода опорных векторов с линейным ядром, было получено по 3 опорных вектора для каждого класса, так же отсутствовали ошибки для тестовых и тренировочных данных. Код программы в приложении 4.1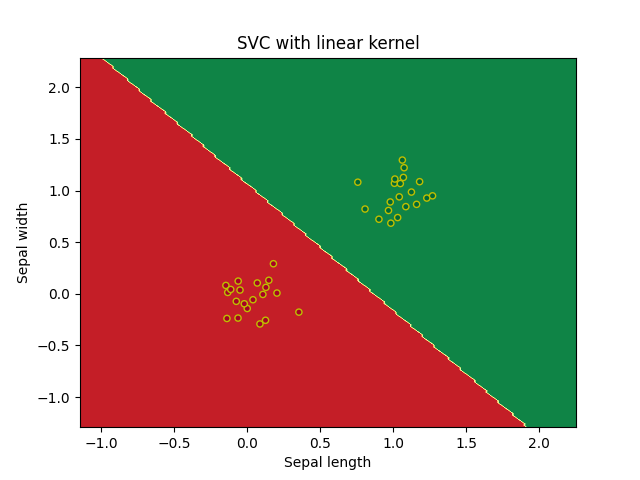

1. 
   ошибок классификации на обучающей и тестовой выборках.
   
2. 
   Постройте алгоритм метода опорных векторов с линейным ядром. Добейтесь нулевой ошибки сначала на обучающей выборке, а затем на тестовой, путем изменения штрафного параметра. Выберите оптимальное значение данного параметра и объясните свой выбор. Всегда ли нужно добиваться минимизации ошибки на обучающей выборке?
   

Для достижения нулевой ошибки на тренировочной выборке пришлось задать штрафной параметр 482.3 были получены следующие графики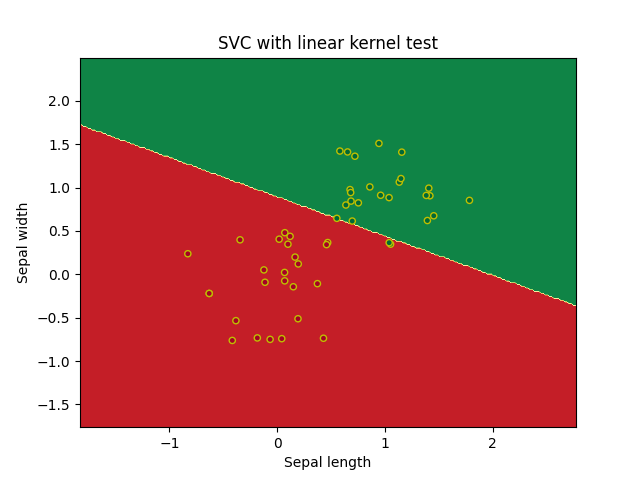



Для получения 0 ошибки на тестовых данных достаточно штрафно1 функции 0.1: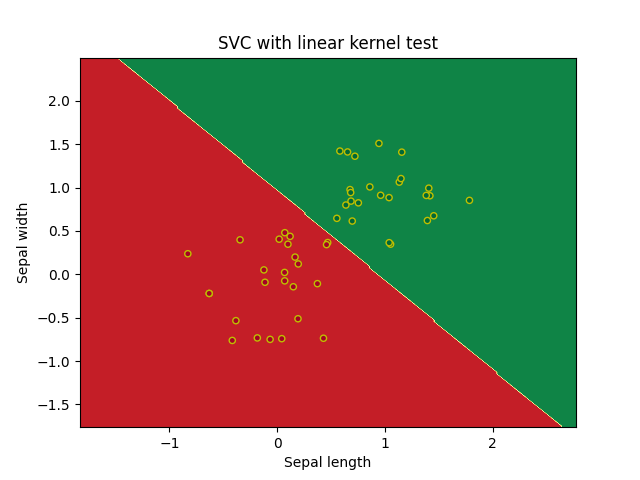



Значениие штрафной функции минимизурующее ошибку до 0 для тестоовой и тренроыочной выборки найдено не было, значение 0.1 можно принять и потимальным для данной классификации так как ошибка на тестовых данных дает результат 0.02, не всегда нужно добавиться минимазации ошибки на тренировочной выборки так как будет страдать результат тестовой, что являесятсе следствиме преобучения. Код прогрммы представлен в приложении 4.2



По результатам обучения на датасете svmdata_c, мы получили неплохие результаты для полиномиальных ядер четной степени, и ядро Гаусса, остальные методы дали рещультат хуже, при этом стоит отметить что использование линейного ядра или ядра с полиномом 1 степени не дает вообще никаого верного результата.



Датасете svmdata_d имеет большие размеры, поэтому даже динейная классификация дает нплохие результаты. Код программы в приложении 4.3

Для датасета svmdata_e были потсроены графики для различных ядер с разными параметрами гамма, при гамма = 1:



Гамма = 10:



Гамма = 100:



Хорошим параметром гамма можно считать 10, при параметре 100 виден эффект переобучения на ядре Гаусса внутри области красных точек появляются области зеленого цвета. Хорошее предсказание дают ядра с полиномами четной степени и ядро Гаусса. Код представлен в приложении 4.4

Классификатор на основе дерева решений.

При параметрах по умолчанию получилось следующие дерево предсказывающие тип стекла по другим признакам, точность предсказания 0.778, глубина дерева 10.

Было проведено исследование зависимости точности классификации от критерия расщепления, максимальной глубины дерева и минимального количества выборок, необходимое для разделения внутреннего узла. Получается, что максимальная глубина дерева не влияет на точность предсказания, но при случайном разбиении могут наблюдаться отклонения, для достижения хорошей точности необходимо не более 15–20, минимального количества выборок, необходимое для разделения внутреннего узла.

Дерево полученное, при помощи параметров по умолчанию можно назвать избыточным так как при подборе гипрепараметров, была получена такая же точность (0.778) но с меньшей глубиной (5).

Код программы в приложении 5.1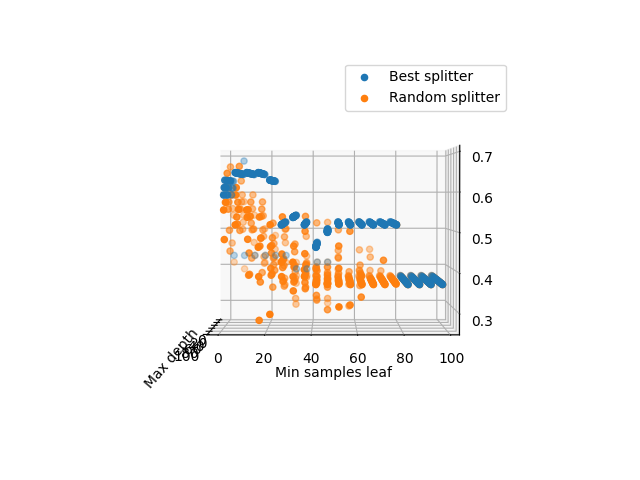

П
ри параметрах по умолчанию на датасете spam7.csv получилось следующие дерево, точность предсказания 0.845, глубина дерева 31.

Для подбора оптисальных параметров был использован тот же алгоритм, что и на датасете glass.csv, была получена точность 0.867, при глубине дерева 6

Таблица ошибок
	Класс спам	Класс не спам
Класс спам	654	33
Класс не спам	119	345

К
ак видно удалось достич маленькой ошибки и небольшего количесвто ложноположительных срабатываний, что важно для отсуствия потерь важных писем. Код программы в приложении 5.2.

Классификация для банка

Выполним классификацию на основе методов k ближайших соседей, опорных векторов и дерева классификаций, будем оценивать точность, recall и False Positive, так как будем считать, что банки не хотят повторения 2008 года и выдают кредиты только тем, кто действительно может их выплатить, ну или по крайней мере большая часть.

Классификатор с 1 соседом имеет точность 0.954, и матрицу ошибок:

Таблица ошибок
	Кредит возвращен	Кредит не возвращен
Кредит возвращен	21952	455
Кредит не возвращен	659	987

Классификатор на опорных векторах я полиномиальным ядром 2 степени имеет точность 0.931, однако матрица ошибок говорит нам о невозможности применения такого классификатор в данной задачи

Таблица ошибок
	Кредит возвращен	Кредит не возвращен
Кредит возвращен	22407	0
Кредит не возвращен	1646	0

Дерево классификации дает точность 0.948, и таблицу ошибок:

Таблица ошибок
	Кредит возвращен	Кредит не возвращен
Кредит возвращен	21903	504
Кредит не возвращен	750	896

Как видно из результатов в данной задачи лучше всего принимать классификатор с k ближайшими соседями он дает лучшую точность среди всех рассмотренных. Код в приложении 6.

Приложения

Приложение 1.1

from sklearn.naive_bayes import GaussianNB
from sklearn.metrics import accuracy_score
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt


dataset = open("tic_tac_toe.txt", "r")
X = list()
y = list()
convert_X = {'x': 1, 'o': 0, 'b': 2}
convert_y = {'positive': 1, 'negative': -1}

for line in dataset:
input_data = line.rstrip('\n').split(',')
X.append(list(map(lambda x: convert_X[x], input_data[:9])))
y.append(convert_y[input_data[-1]])

dataset.close()

train_size = 0.02
GaussianNB_object = GaussianNB()
accuracy_score_of_y_prediction_test = list()
accuracy_score_of_y_prediction_train = list()
list_of_train_sizes = list()
for i in range(0, 49):
list_of_train_sizes.append(train_size)
train_X, test_X, train_y, test_y = train_test_split(X, y, train_size=train_size)
GaussianNB_object.fit(train_X, train_y)
y_prediction_test = GaussianNB_object.predict(test_X)
accuracy_score_of_y_prediction_test.append(accuracy_score(test_y, y_prediction_test))
print("Accuracy test:", accuracy_score_of_y_prediction_test[-1], "train_size=" + str(train_size))
y_prediction_train = GaussianNB_object.predict(train_X)
accuracy_score_of_y_prediction_train.append(accuracy_score(train_y, y_prediction_train))
print("Accuracy train:", accuracy_score_of_y_prediction_train[-1], "train_size=" + str(train_size))
print()
train_size += 0.02

plt.plot(list_of_train_sizes, accuracy_score_of_y_prediction_test, label='Test accuracy')
plt.plot(list_of_train_sizes, accuracy_score_of_y_prediction_train, label='Train accuracy')
plt.xlabel("Train size")
plt.ylabel("Accuracy")
plt.legend()
plt.grid(True)
plt.show()

Приложение 1.2

from sklearn.naive_bayes import GaussianNB
from sklearn.metrics import accuracy_score
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt
import csv
import numpy as np

X = list()
y = list()
convert_y = {'spam': 0, 'nonspam': -1}
with open('spam.csv', newline='') as csvfile:
reader = csv.reader(csvfile, delimiter=',')
reader.__next__()
for row in reader:
X.append(np.array(row[1:-1]).astype(np.float64))
y.append(convert_y[row[-1]])

train_size = 0.02
GaussianNB_object = GaussianNB()
accuracy_score_of_y_prediction_test = list()
accuracy_score_of_y_prediction_train = list()
list_of_train_sizes = list()
for i in range(0, 49):
list_of_train_sizes.append(train_size)
train_X, test_X, train_y, test_y = train_test_split(X, y, train_size=train_size)
GaussianNB_object.fit(train_X, train_y)
y_prediction_test = GaussianNB_object.predict(test_X)
accuracy_score_of_y_prediction_test.append(accuracy_score(test_y, y_prediction_test))
print("Accuracy test:", accuracy_score_of_y_prediction_test[-1], "train_size=" + str(train_size))
y_prediction_train = GaussianNB_object.predict(train_X)
accuracy_score_of_y_prediction_train.append(accuracy_score(train_y, y_prediction_train))
print("Accuracy train:", accuracy_score_of_y_prediction_train[-1], "train_size=" + str(train_size))
print()
train_size += 0.02

plt.plot(list_of_train_sizes, accuracy_score_of_y_prediction_test, label='Test accuracy')
plt.plot(list_of_train_sizes, accuracy_score_of_y_prediction_train, label='Train accuracy')
plt.xlabel("Train size")
plt.ylabel("Accuracy")
plt.legend()
plt.grid(True)
plt.show()

Приложение 2

import math
import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.naive_bayes import GaussianNB
from sklearn.metrics import accuracy_score, auc, f1_score, average_precision_score
from sklearn.metrics import confusion_matrix
from sklearn import metrics


x1_negative = np.random.normal(15, 3, 60)
x2_negative = np.random.normal(9, 3, 60)
x1_positive = np.random.normal(15, math.sqrt(5), 40)
x2_positive = np.random.normal(8, math.sqrt(5), 40)
ax = plt.subplots()
plt.scatter(x1_negative, x2_negative, color='red')
plt.scatter(x1_positive, x2_positive, color='blue')
plt.show()

X = list()
y = list()

for i in range(0, 60):
X.append([x1_negative[i], x2_negative[i]])
y.append(-1)

for i in range(0, 40):
X.append([x1_positive[i], x2_positive[i]])
y.append(1)

train_X, test_X, train_y, test_y = train_test_split(X, y, train_size=0.8)
GaussianNB_object = GaussianNB()
GaussianNB_object.fit(train_X, train_y)
y_prediction_test = GaussianNB_object.predict(test_X)
y_prediction_proba_test = GaussianNB_object.predict_proba(test_X)
accuracy = accuracy_score(test_y, y_prediction_test)
confusion_matrix = confusion_matrix(test_y, y_prediction_test)
print(accuracy)
print(confusion_matrix)
fpr, tpr, _ = metrics.roc_curve(test_y, y_prediction_proba_test[:, 1])
roc_auc = auc(fpr, tpr)

plt.plot(fpr, tpr, color='darkorange',
label='ROC кривая (area = %0.2f)' % roc_auc)
plt.plot([0, 1], [0, 1], color='navy', linestyle='-', label='Random Gauss')
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.0])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('ROC-кривая')
plt.legend(loc="lower right")
plt.show()


precision, recall, _ = metrics.precision_recall_curve(test_y, y_prediction_proba_test[:, 1])
f1 = f1_score(test_y, y_prediction_test)
auc = auc(recall, precision)
ap = average_precision_score(test_y, y_prediction_proba_test[:, 1])
print('F1=%.3f auc=%.3f ap=%.3f' % (f1, auc, ap))
plt.plot([0, 1], [0.5, 0.5], linestyle='--', color='navy', label='Random choice')
plt.plot(recall, precision, color='darkorange', marker='.', label='PR-curve')
plt.xlabel('Recall')
plt.ylabel('Precision')
plt.title('PR-кривая')
plt.legend()
plt.show()

Приложение 3

from sklearn.metrics import accuracy_score
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt
import csv
import numpy as np
from sklearn.neighbors import KNeighborsClassifier

X = list()
y = list()
convert_y = {'spam': 0, 'nonspam': -1}
with open('glass.csv', newline='') as csvfile:
reader = csv.reader(csvfile, delimiter=',')
reader.__next__()
for row in reader:
X.append(np.array(row[1:-1]).astype(np.float64))
y.append(np.array(row[-1]).astype(np.int64))

train_X, test_X, train_y, test_y = train_test_split(X, y, train_size=0.75)
classes = np.zeros(7).astype(np.int64)
accuracy_score_of_y_prediction_test = list()
accuracy_score_of_y_prediction_train = list()
count_neighbors = list()

for neighbors in range(1, 16):
count_neighbors.append(neighbors)
KNeighborsClassifier_object = KNeighborsClassifier(n_neighbors=neighbors)
KNeighborsClassifier_object.fit(train_X, train_y)
y_prediction_test = KNeighborsClassifier_object.predict(test_X)
accuracy_score_of_y_prediction_test.append(accuracy_score(test_y, y_prediction_test))
y_prediction_train = KNeighborsClassifier_object.predict(train_X)
accuracy_score_of_y_prediction_train.append(accuracy_score(train_y, y_prediction_train))
prediction = KNeighborsClassifier_object.predict([[1.516, 11.7, 1.01, 1.19, 72.59, 0.43, 11.44, 0.02, 0.1]])
classes[prediction[0] - 1] += 1
print(classes)


plt.plot(count_neighbors, accuracy_score_of_y_prediction_test, label='Test accuracy')
plt.plot(count_neighbors, accuracy_score_of_y_prediction_train, label='Train accuracy')
plt.xlabel("Count neighbors")
plt.ylabel("Accuracy")
plt.legend()
plt.grid(True)
plt.show()


classes = np.zeros(7).astype(np.int64)
for metric in ['euclidean', 'manhattan', 'chebyshev', 'minkowski']:
KNeighborsClassifier_object = KNeighborsClassifier(metric=metric)
KNeighborsClassifier_object.fit(train_X, train_y)
y_prediction_test = KNeighborsClassifier_object.predict(test_X)
print(accuracy_score(test_y, y_prediction_test))
prediction = KNeighborsClassifier_object.predict([[1.516, 11.7, 1.01, 1.19, 72.59, 0.43, 11.44, 0.02, 0.1]])
classes[prediction[0] - 1] += 1

print(classes)

Приложение 4.1

import matplotlib.pyplot as plt
import numpy as np
from sklearn import svm
from sklearn.metrics import accuracy_score
from sklearn.metrics import confusion_matrix


def make_meshgrid(x, y, h=.02):
x_min, x_max = x.min() - 1, x.max() + 1
y_min, y_max = y.min() - 1, y.max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, h),
np.arange(y_min, y_max, h))
return xx, yy


def read_from_file(file):
X = list()
y = list()
convert_y = {'red': -1, 'green': 1}
for line in file.readlines()[1:]:
input_data = line.rstrip('\n').split('\t')
X.append(input_data[1:-1])
y.append(convert_y[input_data[-1]])
return np.array(X).astype(np.float64), np.array(y).astype(np.int64)


dataset = open("svmdata_a.txt", "r")
train_X, train_y = read_from_file(dataset)

testfile = open("svmdata_a_test.txt", "r")
test_X, test_y = read_from_file(testfile)

clf1 = svm.SVC(kernel='linear')

clf1.fit(train_X, train_y)

clf_predictions = clf1.predict(test_X)
print("Test", accuracy_score(test_y, clf_predictions))
c_matrix = confusion_matrix(test_y, clf_predictions)
print(c_matrix)

clf_predictions = clf1.predict(train_X)
print("Train", accuracy_score(train_y, clf_predictions))
c_matrix = confusion_matrix(train_y, clf_predictions)
print(c_matrix)
print("Support vec ", clf1.n_support_)

X = train_X
y = train_y
X0, X1 = X[:, 0], X[:, 1]
xx, yy = make_meshgrid(X0, X1)
Z = clf1.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
plt.contourf(xx, yy, Z, cmap=plt.cm.RdYlGn)
plt.scatter(X0, X1, c=y, cmap=plt.cm.RdYlGn, s=20, edgecolors='y')
plt.xlim(xx.min(), xx.max())
plt.ylim(yy.min(), yy.max())
plt.xlabel('Sepal length')
plt.ylabel('Sepal width')
plt.title('SVC with linear kernel')
plt.show()

Приложение 4.2

import matplotlib.pyplot as plt
import numpy as np
from sklearn import svm
from sklearn.metrics import accuracy_score
from sklearn.metrics import confusion_matrix


def make_meshgrid(x, y, h=.02):
x_min, x_max = x.min() - 1, x.max() + 1
y_min, y_max = y.min() - 1, y.max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, h),
np.arange(y_min, y_max, h))
return xx, yy


def read_from_file(file):
X = list()
y = list()
convert_y = {'red': -1, 'green': 1}
for line in file.readlines()[1:]:
input_data = line.rstrip('\n').split('\t')
X.append(input_data[1:-1])
y.append(convert_y[input_data[-1]])
return np.array(X).astype(np.float64), np.array(y).astype(np.int64)

def make_grafic(train_X, train_y, test_X, test_y, c, name):
clf1 = svm.SVC(kernel='linear', C=c)
clf1.fit(train_X, train_y)
X = test_X
y = test_y
X0, X1 = X[:, 0], X[:, 1]
xx, yy = make_meshgrid(X0, X1)
Z = clf1.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
plt.contourf(xx, yy, Z, cmap=plt.cm.RdYlGn)
plt.scatter(X0, X1, c=y, cmap=plt.cm.RdYlGn, s=20, edgecolors='k')
plt.xlim(xx.min(), xx.max())
plt.ylim(yy.min(), yy.max())
plt.xlabel('Sepal length')
plt.ylabel('Sepal width')
plt.title('SVC with linear kernel ' + name)
plt.show()

dataset = open("svmdata_b.txt", "r")
train_X, train_y = read_from_file(dataset)

testfile = open("svmdata_b_test.txt", "r")
test_X, test_y = read_from_file(testfile)


c = 0.1
c_test = list()
c_train = list()
c_optimal = list()
for i in range(10000):
clf1 = svm.SVC(kernel='linear', C=c)
clf1.fit(train_X, train_y)
clf_predictions1 = clf1.predict(test_X)
if accuracy_score(test_y, clf_predictions1) == 1.0:
c_test.append(c)
clf_predictions2 = clf1.predict(train_X)
if accuracy_score(train_y, clf_predictions2) == 1.0:
c_train.append(c)
c += 0.1

print(c_train[0])
print(c_test[0])

make_grafic(train_X, train_y, train_X, train_y, c_train[0], 'train')
make_grafic(train_X, train_y, test_X, test_y, c_train[0], 'test')
make_grafic(train_X, train_y, train_X, train_y, c_test[0], 'train')
make_grafic(train_X, train_y, test_X, test_y, c_test[0], 'test')

Приложение 4.3

import matplotlib.pyplot as plt
import numpy as np
from sklearn import svm


def make_meshgrid(x, y, h=.02):
x_min, x_max = x.min() - 1, x.max() + 1
y_min, y_max = y.min() - 1, y.max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, h),
np.arange(y_min, y_max, h))
return xx, yy

def plot_contours(ax, clf, xx, yy, **params):
Z = clf.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
out = ax.contourf(xx, yy, Z, **params)
return out

def read_from_file(file):
X = list()
y = list()
convert_y = {'red': -1, 'green': 1}
for line in file.readlines()[1:]:
input_data = line.rstrip('\n').split('\t')
X.append(input_data[1:-1])
y.append(convert_y[input_data[-1]])
return np.array(X).astype(np.float64), np.array(y).astype(np.int64)


def execute_task(name_file):
dataset = open(name_file + ".txt", "r")
train_X, train_y = read_from_file(dataset)

testfile = open(name_file + "_test.txt", "r")
test_X, test_y = read_from_file(testfile)

C = 1
models = (
svm.SVC(kernel='linear', C=C),
svm.SVC(kernel='poly', degree=1, gamma='auto', C=C),
svm.SVC(kernel='poly', degree=2, gamma='auto', C=C),
svm.SVC(kernel='poly', degree=3, gamma='auto', C=C),
svm.SVC(kernel='poly', degree=4, gamma='auto', C=C),
svm.SVC(kernel='poly', degree=5, gamma='auto', C=C),
svm.SVC(kernel="sigmoid"),
svm.SVC(kernel='rbf', C=C))

models = (clf.fit(train_X, train_y) for clf in models)
titles = (
"SVC with linear kernel",
"SVC with poly kernel (degree=1)",
"SVC with poly kernel (degree=2)",
"SVC with poly kernel (degree=3)",
"SVC with poly kernel (degree=4)",
"SVC with poly kernel (degree=5)",
"SVC with sigmoid kernel",
"SVC with rbf kernel",
)

fig, sub = plt.subplots(4, 2, figsize=(8, 8))
plt.subplots_adjust(wspace=0.4, hspace=0.4)
X0, X1 = test_X[:, 0], test_X[:, 1]
xx, yy = make_meshgrid(X0, X1)

for clf, title, ax in zip(models, titles, sub.flatten()):
plot_contours(ax, clf, xx, yy, cmap=plt.cm.RdYlGn, alpha=0.8)
ax.scatter(X0, X1, c= test_y, cmap=plt.cm.RdYlGn, s=20, edgecolors="y")
ax.set_xlim(xx.min(), xx.max())
ax.set_ylim(yy.min(), yy.max())
ax.set_xlabel("Sepal length")
ax.set_ylabel("Sepal width")
ax.set_xticks(())
ax.set_yticks(())
ax.set_title(title)

plt.grid()
plt.show()


execute_task("svmdata_c")
execute_task("svmdata_d")

Приложение 4.4

import matplotlib.pyplot as plt
import numpy as np
from sklearn import svm


def make_meshgrid(x, y, h=.02):
x_min, x_max = x.min() - 1, x.max() + 1
y_min, y_max = y.min() - 1, y.max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, h),
np.arange(y_min, y_max, h))
return xx, yy

def plot_contours(ax, clf, xx, yy, **params):
Z = clf.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
out = ax.contourf(xx, yy, Z, **params)
return out

def read_from_file(file):
X = list()
y = list()
convert_y = {'red': -1, 'green': 1}
for line in file.readlines()[1:]:
input_data = line.rstrip('\n').split('\t')
X.append(input_data[1:-1])
y.append(convert_y[input_data[-1]])
return np.array(X).astype(np.float64), np.array(y).astype(np.int64)


dataset = open("svmdata_e.txt", "r")
train_X, train_y = read_from_file(dataset)

testfile = open("svmdata_e_test.txt", "r")
test_X, test_y = read_from_file(testfile)

C = 1
for gamma in [1, 10, 100]:
models = (
svm.SVC(kernel='poly', degree=1, gamma=gamma, C=C),
svm.SVC(kernel='poly', degree=2, gamma=gamma, C=C),
svm.SVC(kernel='poly', degree=3, gamma=gamma, C=C),
svm.SVC(kernel='poly', degree=4, gamma=gamma, C=C),
svm.SVC(kernel='poly', degree=5, gamma=gamma, C=C),
svm.SVC(kernel='poly', degree=6, gamma=gamma, C=C),
svm.SVC(kernel="sigmoid", gamma=gamma, C=C),
svm.SVC(kernel='rbf', gamma=gamma, C=C))

models = (clf.fit(train_X, train_y) for clf in models)
titles = (
"SVC with poly kernel (degree=1)",
"SVC with poly kernel (degree=2)",
"SVC with poly kernel (degree=3)",
"SVC with poly kernel (degree=4)",
"SVC with poly kernel (degree=5)",
"SVC with poly kernel (degree=6)",
"SVC with sigmoid kernel",
"SVC with rbf kernel",
)

fig, sub = plt.subplots(4, 2, figsize=(8, 8))
plt.subplots_adjust(wspace=0.4, hspace=0.4)
X0, X1 = test_X[:, 0], test_X[:, 1]
xx, yy = make_meshgrid(X0, X1)

for clf, title, ax in zip(models, titles, sub.flatten()):
plot_contours(ax, clf, xx, yy, cmap=plt.cm.RdYlGn, alpha=0.8)
ax.scatter(X0, X1, c=test_y, cmap=plt.cm.RdYlGn, s=20, edgecolors="y")
ax.set_xlim(xx.min(), xx.max())
ax.set_ylim(yy.min(), yy.max())
ax.set_xlabel("Sepal length")
ax.set_ylabel("Sepal width")
ax.set_xticks(())
ax.set_yticks(())
ax.set_title(title)

plt.grid()
plt.show()

Приложение 5.1

import pydot
from matplotlib import pyplot as plt
from sklearn import tree
from sklearn.metrics import accuracy_score
from sklearn.model_selection import train_test_split
import csv
import numpy as np
from six import StringIO
from sklearn.tree import DecisionTreeClassifier
import os
os.environ["PATH"] += os.pathsep + 'C:/Users/nikit/Desktop/ML/FirstLab/FirstPart'
X = list()
x_now = list()
convert_y = {'spam': 0, 'nonspam': -1}
with open('glass.csv', newline='') as csvfile:
reader = csv.reader(csvfile, delimiter=',')
reader.__next__()
for row in reader:
X.append(np.array(row[1:-1]).astype(np.float64))
x_now.append(np.array(row[-1]).astype(np.int64))

train_X, test_X, train_y, test_y = train_test_split(X, x_now, train_size=0.75)
clf = DecisionTreeClassifier()
clf.fit(train_X, train_y)
prediction = clf.predict(test_X)
print(accuracy_score(test_y, clf.predict(test_X)))
print(clf.get_depth())
titles = ("Id","RI","Na","Mg","Al","Si","K","Ca","Ba")
classes = ("1", "2", "3", "4", "5", "6", "7")
dot_data = StringIO()
tree.export_graphviz(clf, out_file=dot_data, feature_names=titles, class_names=classes)
graph = pydot.graph_from_dot_data(dot_data.getvalue())
graph[0].write_pdf("predict.pdf")

x = list()
y = list()
accuracy = list()
i = 0
max_accur = 0
max_depth = 0
depth = 0
max_min_samples_leaf = 0
for split in ['best', 'random']:
x_now = list()
y_now = list()
now_accuracy = list();
for j in range(1, 100, 5):
for k in range(2, 100, 5):
x_now.append(j)
y_now.append(k)
clf = DecisionTreeClassifier(splitter=split, max_depth=j, min_samples_leaf =k)
clf.fit(train_X, train_y)
acc = accuracy_score(test_y, clf.predict(test_X))
now_accuracy.append(acc)
if acc > max_accur:
max_accur = acc
depth = clf.get_depth()
max_depth = j
max_min_samples_leaf = k
x.append(x_now)
y.append(y_now)
accuracy.append(now_accuracy)


print("Accuracy:", max_accur)
print("Depth:", depth)
print("Max depth:", max_depth)
print("Max min samples leaf:", max_min_samples_leaf)
fig = plt.figure()
ax = plt.axes(projection='3d')
ax.scatter(x[0], y[0], accuracy[0], label='Best splitter')
ax.scatter(x[1], y[1], accuracy[1], label='Random splitter')
plt.xlabel("Max depth")
plt.ylabel("Min samples leaf")
ax.grid()
ax.legend()
plt.show()

Приложение 5.2

import pydot
from matplotlib import pyplot as plt
from sklearn import tree
from sklearn.metrics import accuracy_score, confusion_matrix
from sklearn.model_selection import train_test_split
import csv
import numpy as np
from six import StringIO
from sklearn.tree import DecisionTreeClassifier


import os
os.environ["PATH"] += os.pathsep + 'C:/Users/nikit/Desktop/ML/FirstLab/FirstPart'
X = list()
x_now = list()
convert_y = {'y': 1, 'n': 0}
with open('spam7.csv', newline='') as csvfile:
reader = csv.reader(csvfile, delimiter=',')
reader.__next__()
for row in reader:
X.append(np.array(row[0:-1]).astype(np.float64))
x_now.append(np.array(convert_y[row[-1]]).astype(np.int64))

train_X, test_X, train_y, test_y = train_test_split(X, x_now, train_size=0.75)
clf = DecisionTreeClassifier()
clf.fit(train_X, train_y)
prediction = clf.predict(test_X)
print(accuracy_score(test_y, clf.predict(test_X)))
print(clf.get_depth())
dot_data = StringIO()
tree.export_graphviz(clf, out_file=dot_data)
graph = pydot.graph_from_dot_data(dot_data.getvalue())
graph[0].write_pdf("predict.pdf")
graph[0].write_jpg("predict.jpg")

x = list()
y = list()
accuracy = list()
i = 0
max_accur = 0
max_depth = 0
depth = 0
max_min_samples_leaf = 0
confusion_matrixes = list()
for split in ['best', 'random']:
x_now = list()
y_now = list()
now_accuracy = list();
for j in range(1, 100, 5):
for k in range(2, 100, 5):
x_now.append(j)
y_now.append(k)
clf = DecisionTreeClassifier(splitter=split, max_depth=j, min_samples_leaf =k)
clf.fit(train_X, train_y)
predict = clf.predict(test_X);
acc = accuracy_score(test_y, predict)
now_accuracy.append(acc)
if acc > max_accur:
max_accur = acc
depth = clf.get_depth()
max_depth = j
max_min_samples_leaf = k
dot_data = StringIO()
tree.export_graphviz(clf, out_file=dot_data)
graph = pydot.graph_from_dot_data(dot_data.getvalue())
graph[0].write_jpg("predict_best.jpg")
confusion_matrixes.append(confusion_matrix(test_y,predict))
x.append(x_now)
y.append(y_now)
accuracy.append(now_accuracy)


print("Accuracy:", max_accur)
print("Depth:", depth)
print("Max depth:", max_depth)
print("Max min samples leaf:", max_min_samples_leaf)
print(confusion_matrixes[-1])
fig = plt.figure()
ax = plt.axes(projection='3d')
ax.scatter(x[0], y[0], accuracy[0], label='Best splitter')
ax.scatter(x[1], y[1], accuracy[1], label='Random splitter')
plt.xlabel("Max depth")
plt.ylabel("Min samples leaf")
ax.grid()
ax.legend()
plt.show()

Приложение 6

from sklearn import svm
from sklearn.metrics import accuracy_score, confusion_matrix
import csv
import numpy as np
from sklearn.neighbors import KNeighborsClassifier
from sklearn.tree import DecisionTreeClassifier


def read_from_file(file_name):
X = list()
y = list()
with open(file_name, newline='') as csvfile:
reader = csv.reader(csvfile, delimiter='\t')
reader.__next__()
for row in reader:
X.append(np.array(row[1:]).astype(np.float64))
y.append(np.array(row[0]).astype(np.int64))
return np.array(X).astype(np.float64), np.array(y).astype(np.int64)


train_X, train_y = read_from_file('bank_scoring_train.csv')
test_X, test_y = read_from_file('bank_scoring_test.csv')

#k ближайшихсоседей
best_matrix = 0
count_neighbors = 0
best_accur = 0
for neighbors in range(1, 8):
KNeighborsClassifier_object = KNeighborsClassifier(n_neighbors=neighbors)
KNeighborsClassifier_object.fit(train_X, train_y)
prediction = KNeighborsClassifier_object.predict(test_X)
acc = accuracy_score(test_y, prediction)
if acc > best_accur:
best_accur = acc
best_matrix = confusion_matrix(test_y,prediction)
count_neighbors = neighbors

print(best_accur)
print(best_matrix)
print(count_neighbors)


# опорныевекторалинейноеядро
clf = svm.SVC(kernel='poly', degree=2)
clf.fit(train_X, train_y)
prediction = clf.predict(test_X)
print(accuracy_score(test_y, prediction))
print(confusion_matrix(test_y,prediction))


#деревоклассификации
best_matrix = 0
best_accur = 0
best_matrix = 0
for split in ['best', 'random']:
x_now = list()
y_now = list()
now_accuracy = list()
for j in range(1, 100, 5):
for k in range(2, 100, 5):
x_now.append(j)
y_now.append(k)
clf = DecisionTreeClassifier(splitter=split, max_depth=j, min_samples_leaf =k)
clf.fit(train_X, train_y)
predict = clf.predict(test_X)
acc = accuracy_score(test_y, predict)
now_accuracy.append(acc)
if acc > best_accur:
best_accur = acc
best_depth = clf.get_depth()
best_matrix = confusion_matrix(test_y,predict)

print(best_accur)
print(best_matrix)
print(best_depth)

Санкт-Петербург 2022