Опытная проверка методов расчета цепей постоянного тока. Отчет по лабораторной работе 1 Опытная проверка методов расчета цепей постоянного тока
 Скачать 0.95 Mb. Скачать 0.95 Mb.
|
|
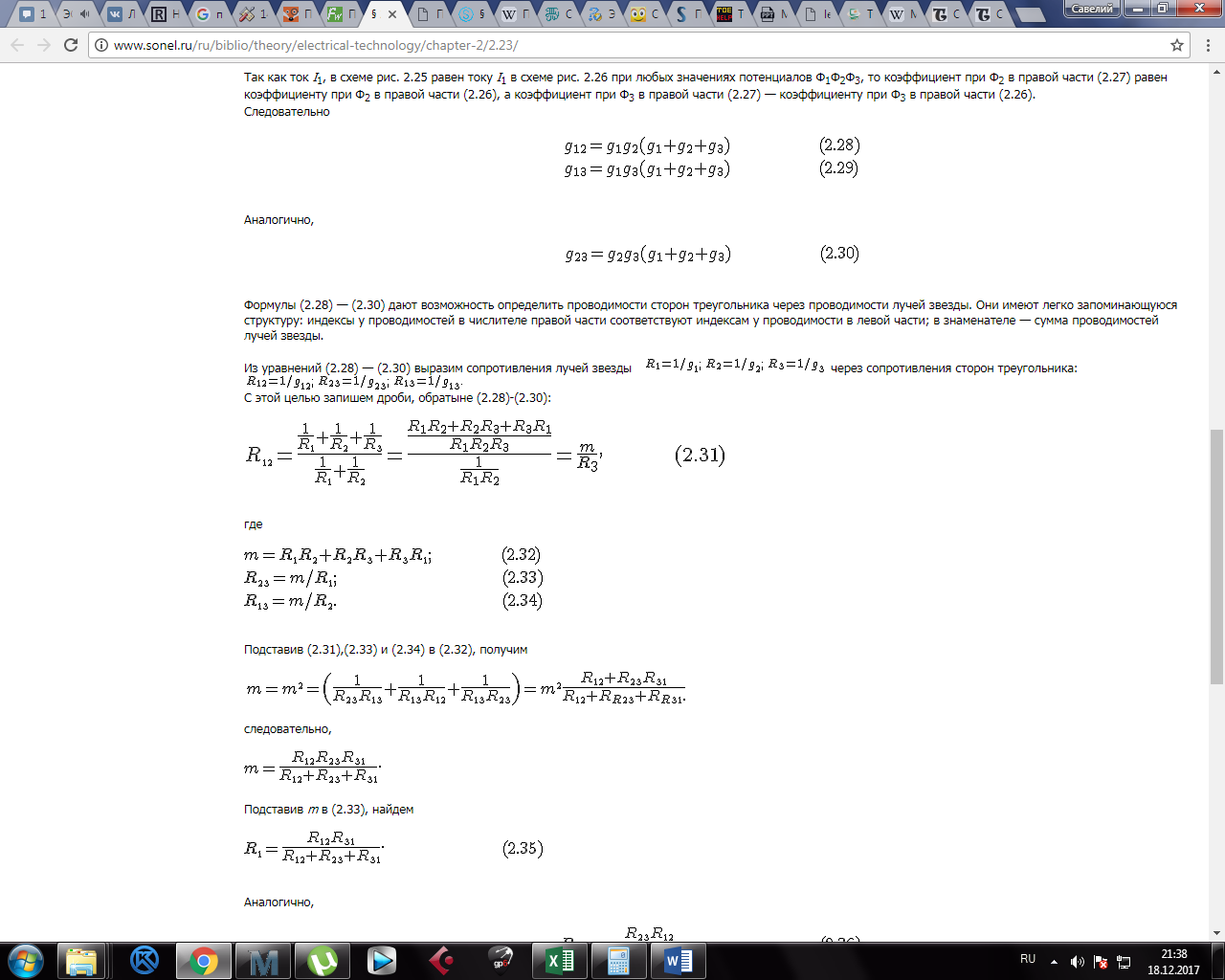
Министерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Пермский национальный исследовательский политехнический университет» Кафедра: Конструирование и технологии в электротехнике Отчет по лабораторной работе №1 «Опытная проверка методов расчета цепей постоянного тока» Выполнил студент гр. ЭС-16-1б Сальников С.В. Проверил преподаватель Кулютникова Е.А. Пермь, 2017 Цель работы Экспериментальная проверка эквивалентности преобразования пассивных электрических цепей, законов Кирхгофа, методов наложения и узловых потенциалов. Обработка результатов измерений Результаты представлены в таблице. А) Значения сопротивлений с помощью закона Ома 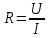 R3=969.31 Ом (R3=Uac/I3 рис 1.2 данные взяты из таблицы 1.1) R5=213.9 Ом (R5= Uab/I5 рис 1.2 данные взяты из таблицы 1.1 ) R4=976 Ом (R4= Ubc/I4 рис 1.2 данные взяты из таблицы 1.1) R2=9500 Ом (R2= Ubc/I2 рис 1.2 данные взяты из таблицы 1.1 ) R1=986.4 Ом (R1= Uac/I1 рис 1.3 данные взяты из таблицы 1.1 ) E1=14.82 В E2=10 В Б) Физические направления тока указаны на схеме. 3. Проверка выполнения законов Кирхгофа и баланса мощности для каждой цепи. Первая цепь: 1 ЗК т.А 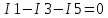 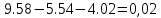 неточность связана с погрешностью приборов. неточность связана с погрешностью приборов.т.B 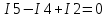 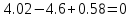 т.C 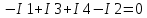 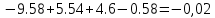 2 ЗК Iк: 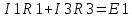 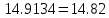 IIк: 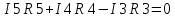 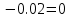 IIIк 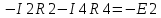 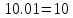 Баланс мощности 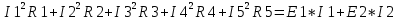 Pист=0,14817 Вт Pпот=0.14777 Вт Метод Наложения для первой цепи Оставим источник E1 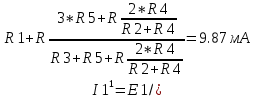 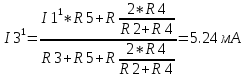 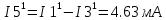 по 1 ЗК по 1 ЗК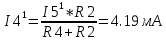 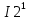 = =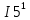 - -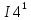 =0.44 мА по 1 ЗК =0.44 мА по 1 ЗКОставим источник E2 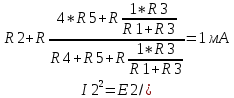 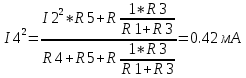 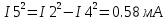 по 1 ЗК по 1 ЗК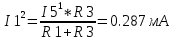 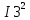 = =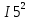 - -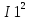 =0.293 мА по 1 ЗК =0.293 мА по 1 ЗКСложим полученные значение в соответствии с истинным направлением тока. 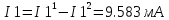 (ток совпадает с направлением тока на схеме 1.1) (ток совпадает с направлением тока на схеме 1.1) 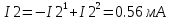 (ток совпадает с направлением тока на схеме 1.1) (ток совпадает с направлением тока на схеме 1.1)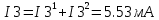 (ток совпадает с направлением тока на схеме 1.1) (ток совпадает с направлением тока на схеме 1.1)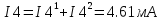 (ток совпадает с направлением тока на схеме 1.1) (ток совпадает с направлением тока на схеме 1.1)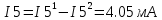 (ток совпадает с направлением тока на схеме 1.1 (ток совпадает с направлением тока на схеме 1.1Метод контурных токов Составим систему для данной цепи 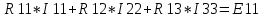 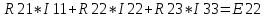 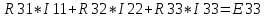 R11=R1+R3 E11=E1 R12=R21=-R3 E22=0 R13=R31=0 E33=E2 R22=R3+R4+R5 R33=R2+R4 R23=R32=-R4 I11=0.0095797332688551965002 [A] I22=0.0040391414008240875958 [A] I33=-0.00057825486758263559627 [A] I1=I11=0.009579 [A] I2=I33=0.000578254 [A] I3=I11-I22=0.00554 [A] I4=I22-I33=0.004617 [A] I5=I22=0.00403914 [A] Рист=E1*I1+E2*I2=0.147754195720260368095239 [Bт] Pпот= 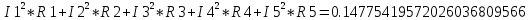 [Bт] [Bт]      I245 I34 I135 Э  квивалентное преобразование для цепи 1.1 квивалентное преобразование для цепи 1.1 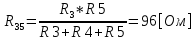 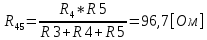 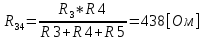 R2=9500 Ом R1=986.4 Ом R135=R1+R35=1083.1 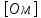 R245= R2+R45=9596.7 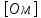 E1=14.82 В E2=10 В Заземлим точку С 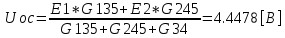 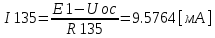 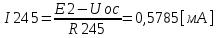 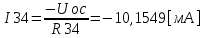 Баланс мощности 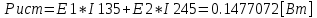 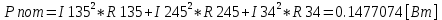 Контрольные вопросы. Принцип суперпозиции— один из самых общих законов во многих разделах физики. В самой простой формулировке принцип суперпозиции гласит: А) Результат воздействия на частицу нескольких внешних сил есть векторная сумма воздействия этих сил. Б) Любое сложное движение можно разделить на два и более простых. Данный принцип лежит в основе метода наложения: сумма действий источников равна сумме действий каждого источника в отдельности. При использовании метода наложения в подсхемах используется замена: источник тока на разрыв цепи, источник ЭДС- накоротко замкнутый участок. Данный метод (наложения) удобно использовать в тех случаях, когда необходимо найти ток лишь в одной ветви. Направления тока в подсхемах выбираем в соответствии с полярностью источника, оставленного в схеме. Рассчитывается ток в данной ветви в каждой подсхеме. Ток в данной ветви в исходной схеме считается как алгебраическая сумма токов подсхем. При суммировании с «+» берутся те токи подсхем, направления которых совпадает с направлением тока в исходной схеме. Если сумма со знаком «+» значит направление тока совпадает с направлением указанным нами в исходной схеме, если с «-», то наоборот. Преобразование считается эквивалентным. Если в результате замены некоторого участка цепи на эквивалентный не изменяется токи и напряжения в непреобразованной части цепи. Последовательное соединение сопротивления при эквивалентный замене суммируются 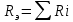 При параллельном соединении пассивных ветвей суммируются их проводимости 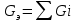 Двум параллельным сопротивлениям эквивалентно сопротивление: 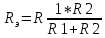 Если каждой из n сопротивлений равно R, то при последовательном их соединении 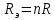 , а при параллельном , а при параллельном 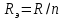 Выразим токи I1, I2 и I33 в звезде и в треугольнике через разности потенциалов точек и соответствующие проводимости. Для звезды
Подставим (2.24) в (2.23) и найдем Φ0: откуда
Аналогично,
Формулы (2.28) — (2.30) дают возможность определить проводимости сторон треугольника через проводимости лучей звезды. Они имеют легко запоминающуюся структуру: индексы у проводимостей в числителе правой части соответствуют индексам у проводимости в левой части; в знаменателе — сумма проводимостей лучей звезды. Из уравнений (2.28) — (2.30) выразим сопротивления лучей звезды С этой целью запишем дроби, обратные (2.28)-(2.30):
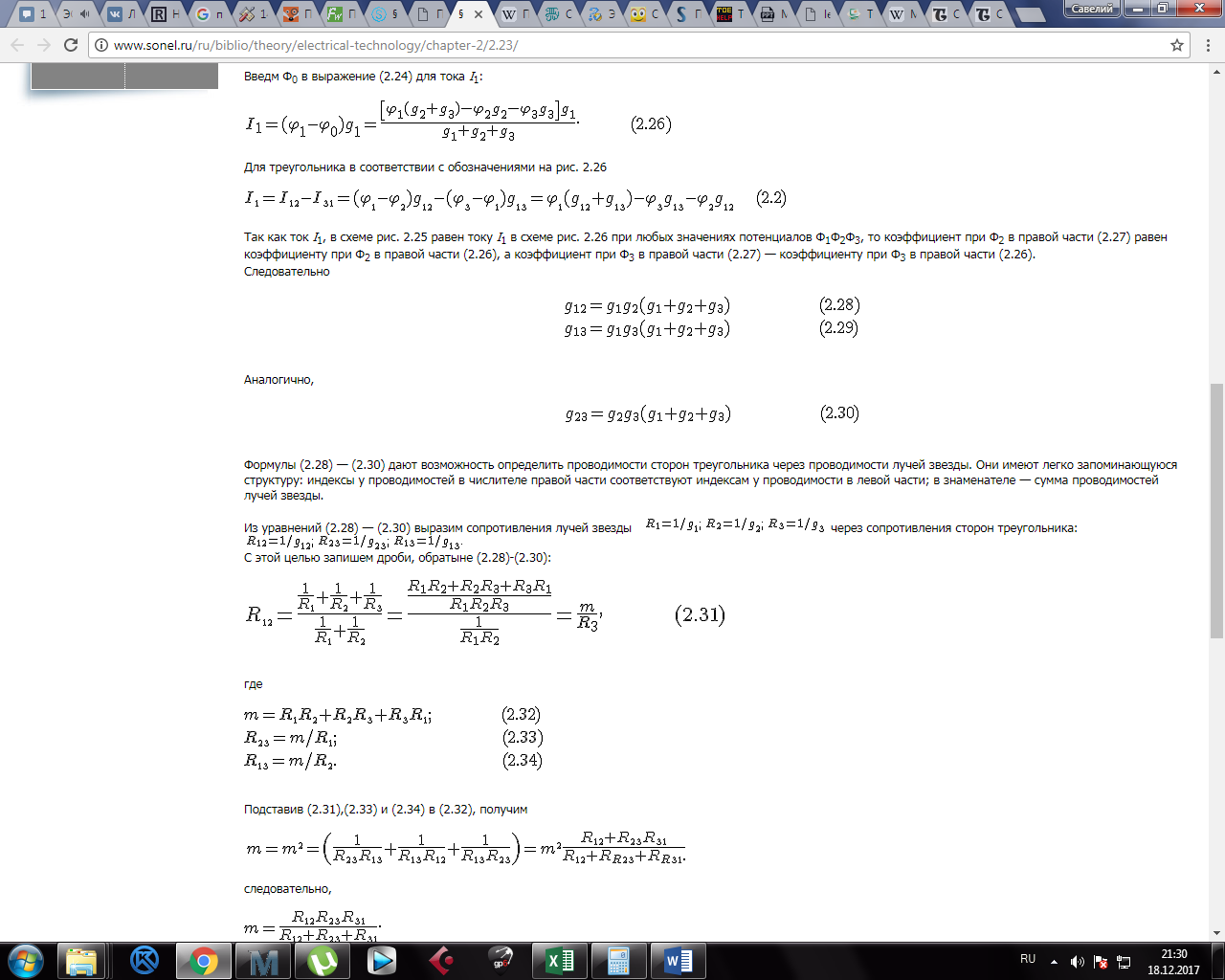 где 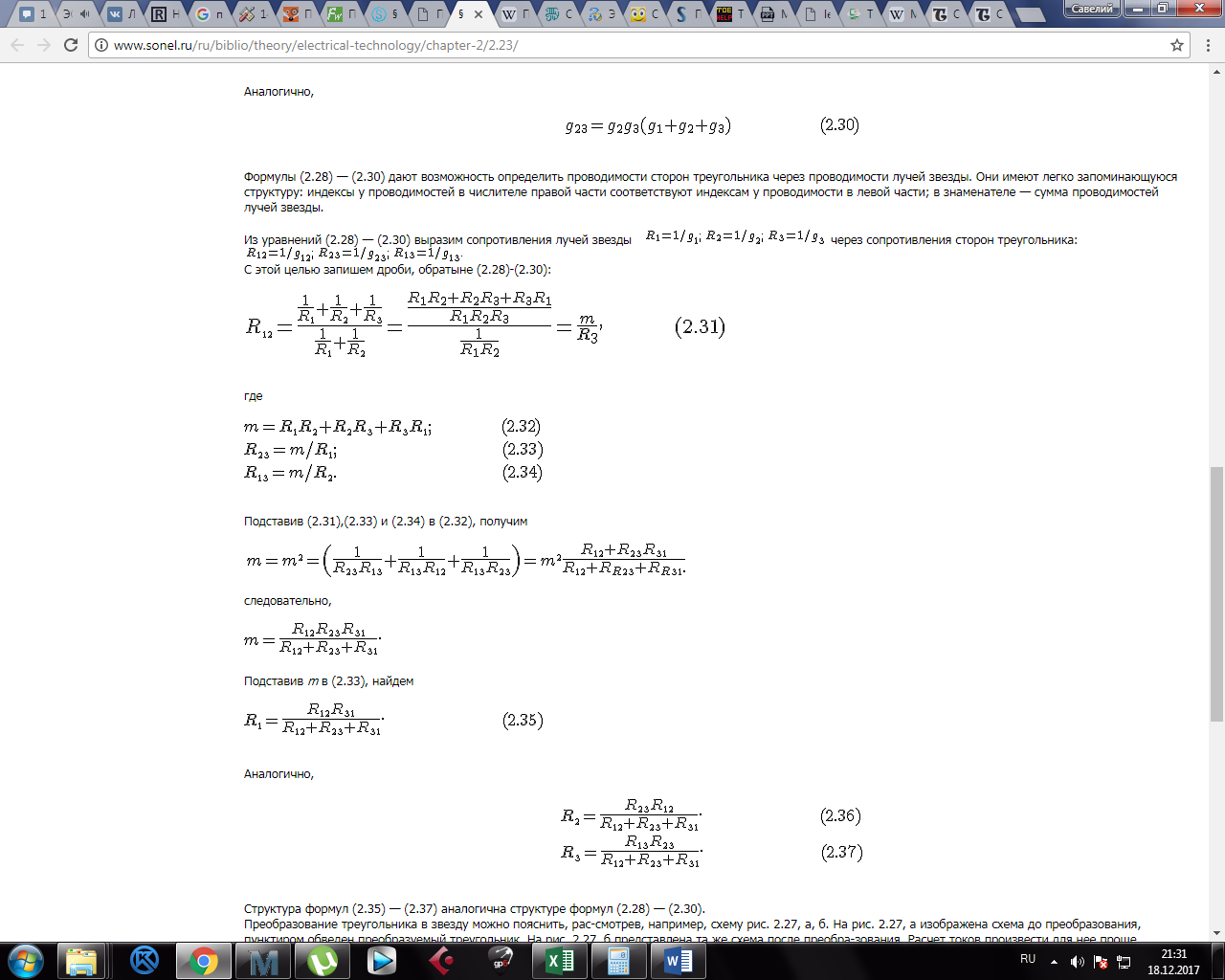
Подставив (2.31),(2.33) и (2.34) в (2.32), получим 
с П
 Аналогично,
Аналогично при обратном преобразовании звезды в треугольник определение проводимостей определяются по формулам. 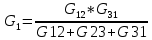 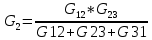 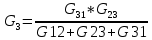 Значение всех коэф-в в методе контурных токов. 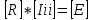 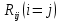 собственное сопротивление контура, определяется как арифметическая сумма сопротивлений, входящих в i-й контур (только с +) собственное сопротивление контура, определяется как арифметическая сумма сопротивлений, входящих в i-й контур (только с +)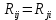 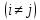 -взаимные или общие сопротивления для i-го и j-го контуров, берутся со знаком «-» если в общий для i-го и j-го контуров ветви, i-й и j-й контурные токи, направление встречно. -взаимные или общие сопротивления для i-го и j-го контуров, берутся со знаком «-» если в общий для i-го и j-го контуров ветви, i-й и j-й контурные токи, направление встречно.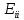 -контурное ЭДС, определяется, ЭДС источников, входящих в контур. Берутся со знаком «-», если источник включается встречно для i-го контурного тока. -контурное ЭДС, определяется, ЭДС источников, входящих в контур. Берутся со знаком «-», если источник включается встречно для i-го контурного тока.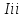 контурной ток i-го контура контурной ток i-го контураЗначение всех коэф-в в методе узловых потенциалов. Собственная проводимость узла (Gii) представляет собой арифметическую сумму проводимостей всех ветвей, соединенных в i-ом узле. Общая проводимость i-ого и j-ого узлов (Gij = Gji) представляет собой взятую со знаком «-» сумму проводимостей ветвей, присоединенных одновременно и i-ому и j-ому узлам. Проводимости ветвей с источниками тока полагаются равными нулю и в собственные и общие проводимости не входят. Узловой ток (Jii) состоит из двух алгебраических сумм: первая содержит токи источников тока, содержащиеся в ветвях, соединенных в i-ом узле; вторая представляет собой произведение ЭДС источников напряжения на проводимости соответствующих ветвей, соединенных в i-ом узле. Со знаком «+» в эту сумму входят E и J источников, действие которых направлено к узлу, со знаком «-» - остальные. | |||||||||||