Отчёт по 1 лабораторной работе. Численные методы. Отчет по лабораторной работе 1 по дисциплине Численные методы и программирование
 Скачать 0.51 Mb. Скачать 0.51 Mb.
|
1. Составление системы уравнений равновесия для плоской системы сил и представление её в матричной форме 1.1 Исходные данные  Рис. 3. Многопролетная балка a=b=c=d=1 м; a = 1 м. e=f=g=h=1,4 м;  = 45 = 45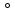 (sin (sin = cos = cos  = 0,707); = 0,707);m= 2 кН*м;  = 30 = 30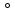 (sin (sin = cos = cos = 0,866); = 0,866); = 7 кН; = 7 кН;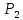 = 14 кН; = 14 кН; = 3 кН; = 3 кН;Q = 2 кН/м; Требуется определить опорные реакции балки  , , , , , , , , 2. Система уравнений равновесия  = 0; = 0;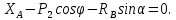  = 0; = 0;   = 0; = 0;   = 0; = 0;   = 0; = 0; 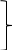 3. Система уравнений равновесия в стандартной форме 3. Система уравнений равновесия в стандартной форме   4. Система уравнений равновесия в матричной форме  5. Блок-схема программы   6. Текст программы решения системы уравнений методом Гаусса и исходных данных на алгоритмическом языке «Q BASIC» OPEN “nx.dat” FOR UNPUT AS#1 OPEN “nx.dat” FOR UNPUT AS#2 OPEN “nx.dat” FOR UNPUT AS#3 OPEN “result.dat” FOR UNPUT AS#4 PRINT #4, PRINT #4, PRINT #4, PRINT #4, PRINT #4, PRINT #4, PRINT #4, PRINT #4, PRINT #4, PRINT #4, PRINT #4, PRINT #4, PRINT #4, PRINT #4, PRINT #4, CLS DIM a(10,10) DIM x(10) DIM b(10) ‘Вводим размерность INPUT #1,n PRINT n FOR i=1 TO n FOR j=1 TO n ‘Вводим матрицу а INPUT #2, a(i,j) NEXT j NEXT i ‘Вводим матрицу в FOR i=1 TO n INPUT #3, b(i) NEXT i PRINT #4, “Количество уравнений”,n PRINT #4, PRINT #4, “Коэффициенты при неизвестных:” FOR i=1 TO n FOR j=1 TO n PRINT #4, a(i,j); PRINT a(i,j); NEXT j PRINT #4, NEXT j PRINT #4, PRINT #4, “Свободные члены уравнений” FOR j=1 TO n PRINT #4, b(j); PRINT b(j); NEXT j PRINT #4, FOR k=1 TO n-1 PRINT k 1=k Max=abs (a(k,k)) PRINT “max=”, max FOR i=k+1 TO n IF max 1=i PRINT “max=”, max max=a(i,k) END IF NEXT i IF 1=k THEN GOTO m2 FOR j=k TO n c=a(r,j) a(k,j)=a(1,j) a(1,j)=c NEXT j c=b(k) b(k)=b(1) b(1)=c m2:FOR j=1 TO n FOR j1=1 TO n NEXT j1 NEXT j FOR i=k+1 TO n d=a(i,k)/a(k,k) a(i,k)=0 FOR i=k+1 TO n a(i,j)=a(i,j) – d*a(k,j) NEXT j b(i)=b(i) – d*b(k) NEXT i FOR i=1 TO n FOR ji=1 TO n NEXT j1 NEXT j NEXT k FOR i=1 TO n FOR j=1 TO n NEXT j NEXT i x(n)=b(n)/a(n,n) ‘Обратный ход FOR i=n-1 TO 1 STEP -1 s=0 FOR j=i+1 To n s=s+a(I,j)*x(j) NEXT j x(j)=(b(i)-s)/a(I,i) NEXT i PRINT “Решение” FOR i=1 TO n PRINT x(i); NEXT i PRINT #4, “Величина неизвестных:” FOR i=1 TO n PRINT #4, x(i); NEXT i Print #4, “” CLOSE  файл nx.dat файл nx.dat   файл ax.dat файл ax.dat   7. Распечатка решения системы уравнений на ПК Количество уравнений: 5 Коэффициенты при неизвестных: Свободные члены уравнений: Величины неизвестных: 8. Проверка правильности решения системы уравнений  = 0; = 0;  = 0; = 0; 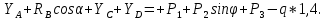  = 0; = 0;   = 0; = 0;   = 0; = 0; |
