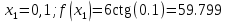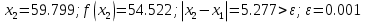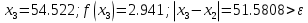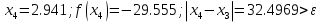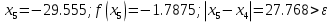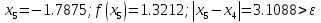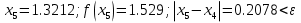чм лаба 1. Отчет по лабораторной работе 1 по дисциплине численные методы
 Скачать 68.33 Kb. Скачать 68.33 Kb.
|
 МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ  ФЕДЕРАЦИИ ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ «МОСКОВСКИЙ АВИАЦИОННЫЙ ИНСТИТУТ (национальный исследовательский университет)» Кафедра «812 Математика» ОТЧЕТ по лабораторной работе №1 по дисциплине численные методы ____________________________________________________________________________________ Скилевая А.О.___________________ 12РКК−4ДБ−323−15____________ Беляков Д.В.____________________ ФИО Студент Группа ФИО Руководитель Работа защищена __________________ Дата «___» _______________ 20___ г. (подпись преподавателя в случае защиты) Москва 2018 Оглавление1.1.Описание 3 1.2.Решение 3 2.1.Описание 5 2.2.Решение 5 3.1. Описание 6 3.2. Решение 6
Метод половинного деления один из методов решения нелинейных уравнений и основан на последовательном сужении интервала, содержащего единственный корень уравнения 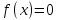 до того времени, пока не будет достигнута заданная точность ɛ. до того времени, пока не будет достигнута заданная точность ɛ.Пусть задан отрезок 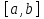 , содержащий один корень уравнения. Предварительно необходимо определить области локализации корней данного уравнения. Если на отрезке , содержащий один корень уравнения. Предварительно необходимо определить области локализации корней данного уравнения. Если на отрезке 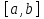 содержится более одного корня, то метод не работает. содержится более одного корня, то метод не работает.
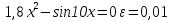 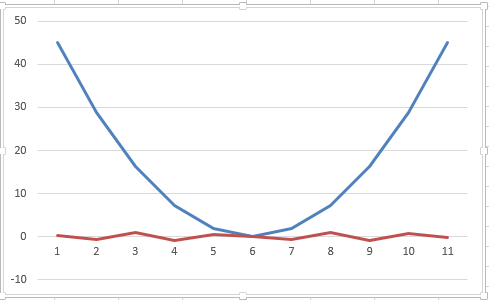 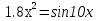 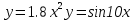 Корень находится в отрезке [ -1 : 1 ]
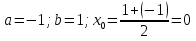 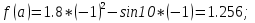 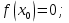 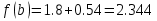
Выбираем искомый корень из отрезка [-1;1] 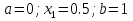 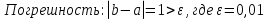
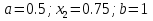 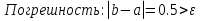
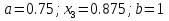 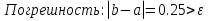
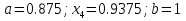 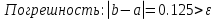
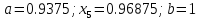 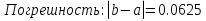
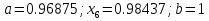 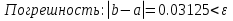 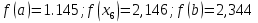 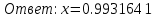
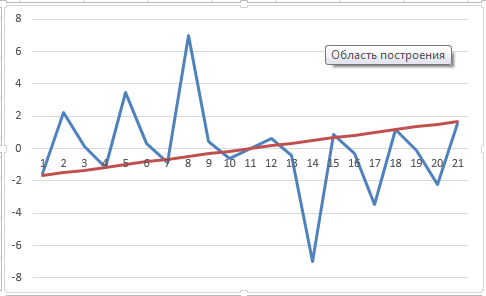
Метод простой итерации — один из простейших численных методов решения уравнений. Метод основан на принципе сжимающего отображения, который применительно к численным методам в общем виде также может называться методом простой итерации или методом последовательных приближений. В частности, для систем линейных алгебраических уравнений существует аналогичный метод итерации.
 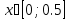 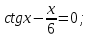 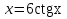 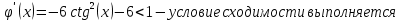 Ответ: 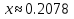 . .3. Метод Ньютона 3.1. ОписаниеМетод Ньютона, алгоритм Ньютона (также известный как метод касательных) — это итерационный численный метод нахождения корня (нуля) заданной функции. Метод был впервые предложен английским физиком, математиком и астрономом Исааком Ньютоном (1643—1727). Поиск решения осуществляется путём построения последовательных приближений и основан на принципах простой итерации. Метод обладает квадратичной сходимостью. Модификацией метода является метод хорд и касательных. Также метод Ньютона может быть использован для решения задач оптимизации, в которых требуется определить ноль первой производной либо градиента в случае многомерного пространства. 3.2. Решение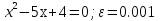 Условие сходимости: 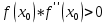 Пусть 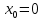 , тогда: , тогда: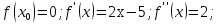 Условие: 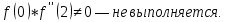 Пусть 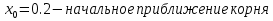 , тогда: , тогда: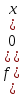 Условие: 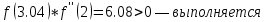 . .Последовательность итераций для метода Ньютона. 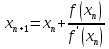 Критерий сходимости: 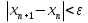 1 итерация: 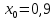 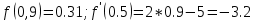 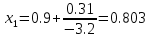 Критерий сходимости: 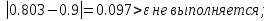 2 итерация: 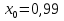 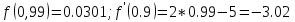 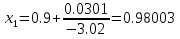 Критерий сходимости: 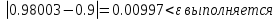 . .Ответ: Приближенное значение уравнения: 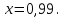 Заключение В результате проделанной работы были изучены новые методы решения линейных уравнений. |