Лаба1. Отчет по лабораторной работе 1 По дисциплине Информатика наименование на тему системы счисления

• Название: Отчет по лабораторной работе 1 По дисциплине Информатика наименование на тему системы счисления
• Дата: 26.01.2023
• Размер: 298.07 Kb.
• Имя файла: Лаба1.docx
• Тип: Отчет; #907234

Министерство науки и высшего образования Российской Федерации

Федеральное государственное бюджетное образовательное учреждение

высшего образования

Воронежский государственный технический университет

Факультет информационных технологий и компьютерной безопасности

Кафедра графики, конструирования и информационных технологий

в промышленном дизайне

ОТЧЕТ ПО ЛАБОРАТОРНОЙ РАБОТЕ № 1

По дисциплине: Информатика

наименование

на тему: СИСТЕМЫ СЧИСЛЕНИЯ

Автор работы: Тельнова А.Ю группа Збист-212

подпись, дата инициалы, фамилия обозначение

Профиль подготовки: 09.03.02 «Информационные системы и технологии»

номер, наименование

Руководитель: асс. О.А. Рябинина

подпись, дата должность, инициалы, фамилия

Воронеж

2022

Цель работы: изучение позиционных систем счисления.

Приборы и принадлежности: компьютер.

Вариант 2

Задание 1. Переведем целые числа из десятичной системы счисления в двоичную (рисунок 1)

1. 
   Разделим десятичное число на 2, получим остаток и частное от деления.
   
2. 
   Переведем остаток от деления в двоичную цифру (двоичная цифра равна остатку).
   
3. 
   Повторим данные шаги, используем частное от деления, пока оно не станет равно 0.
   

Таким способом переведем десятичное число 1052 в двоичную систему :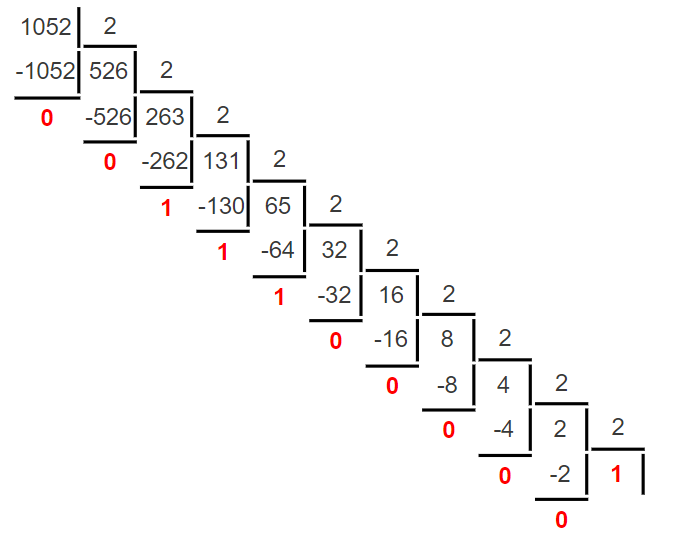

Рисунок 1- из десятичной в двоичную

Получаем, что 1052=10000011100₂

По такому же принципу переведем остальные числа. Переведем 1387 из десятичной в двоичную (рисунок 2):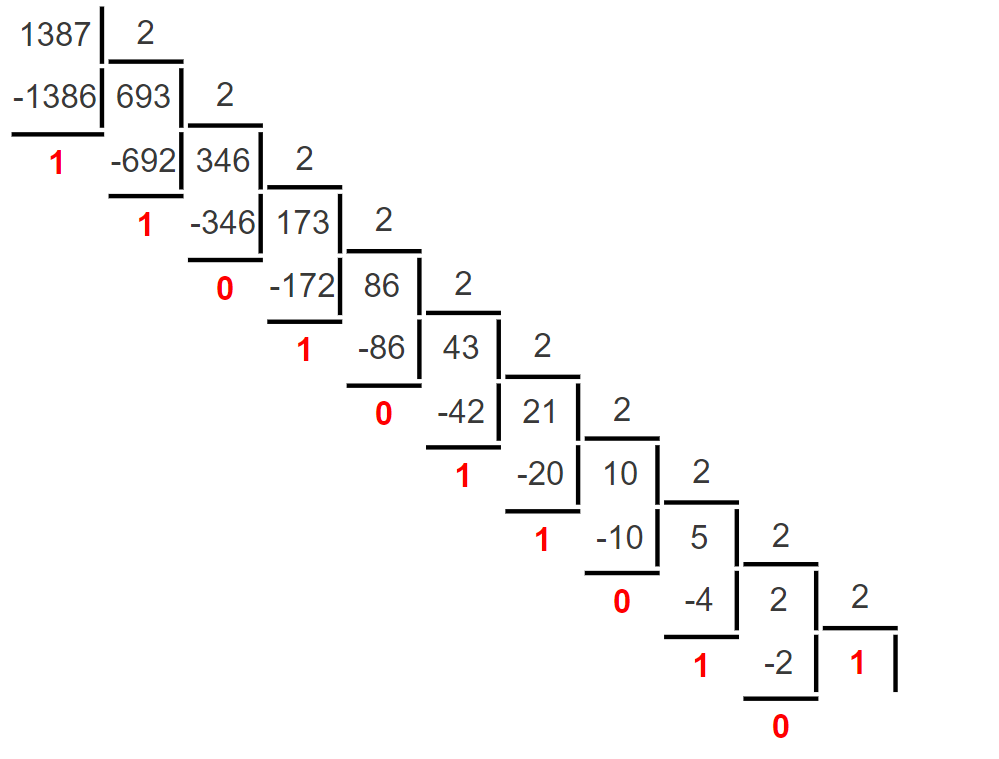



Рисунок 2 – перевод числа 1387

Получим: 10101101011₂

Переведем 7634 из десятичной в двоичную (рисунок 3):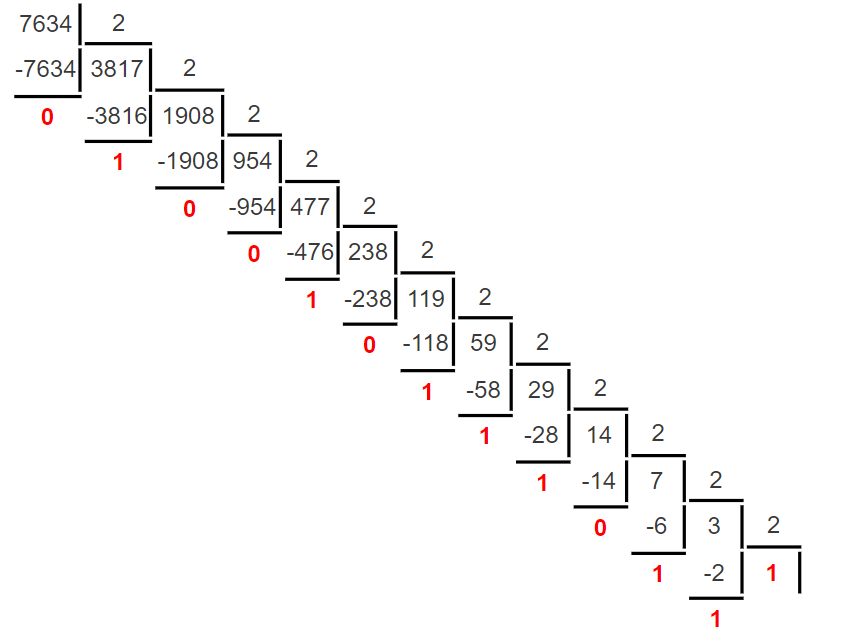



Рисунок 3 – перевод числа 7634 в двоичную.

Эти же числа переведем в восьмеричную систему (рисунок 4):

1.Разделим десятичное число на 8, получим остаток и частное от деления.

2. Запишем остаток в обратном порядке

3. Повторим данные шаги, используйте частное от деления, пока оно не станет равно 0.

Получим: 1387₁₀ = 2553₈

1052₁₀ = 2034₈

7634₁₀ = 16722₈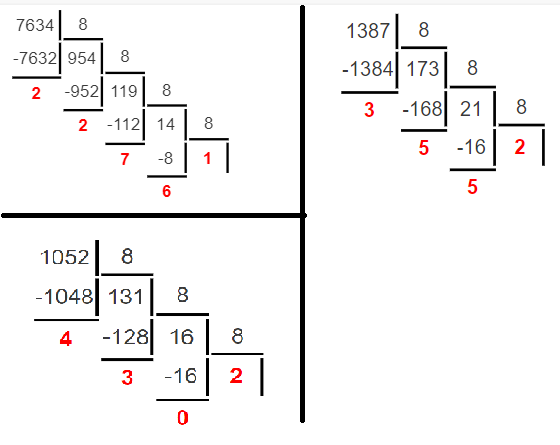



Рисунок 4 – перевод из десятичной в восьмеричную

Эти же числа переведем в шестнадцатеричную систему (рисунок 5):

1.Разделим десятичное число на 16, получим остаток и частное от деления.

2. Запишем остаток в обратном порядке с учетом, что числа начиная с 10 нумеруются буквами(A,B,C и тд)

3. Повторим данные шаги, используйте частное от деления, пока оно не станет равно 0.

Получим: 1052₁₀ = 41C₁₆

7634₁₀=1DD2₁₆

1387₁₀=56B₁₆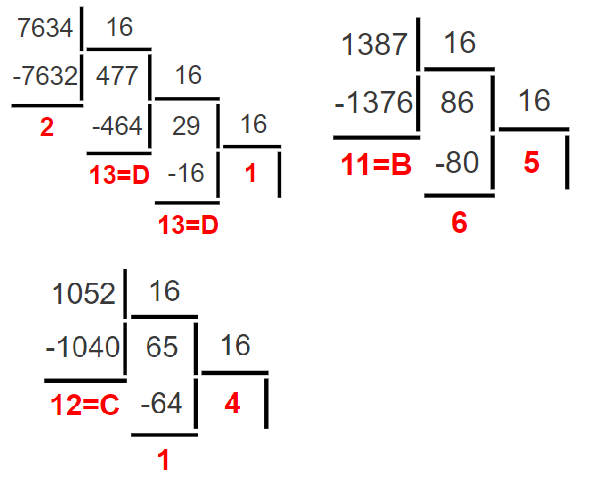



Рисунок 5 – перевод из десятичной в шестнадцатеричную

Задание 2. Переведем целые числа из двоичной системы счисления:

Переведем число 011001₂ в десятичную:

011001₂ = 0∙2⁵+1∙2⁴+1∙2³+0∙2²+0∙2¹+1∙2⁰ = 0+16+8+0+0+1 = 25₁₀

Восьмеричную и шестнадцатеричную после перевода в десятичную (рисунок 6):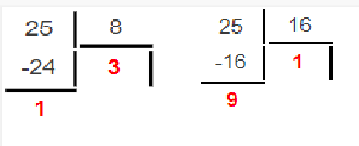



Рисунок 6 – перевод из двоичной в шестнадцатеричную и восьмеричную

Получаем : 011001₂=31₈

011001₂=19₁₆

Переведем 100001₂ в десятичную:

100001₂ = 1∙2⁵+0∙2⁴+0∙2³+0∙2²+0∙2¹+1∙2⁰ = 32+0+0+0+0+1 = 33₁₀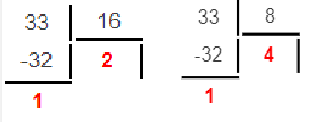

Переведем 100001₂ в восьмеричную и шестнадцатеричную систему (рисунок 7):


Рисунок 7 – перевод в восьмеричную и шестнадцатеричную систему

Получаем: 100001₂=21₁₆

100001₂=41₈

Переведем 001001₂ в десятичную :

001001₂ = 0∙2⁵+0∙2⁴+1∙2³+0∙2²+0∙2¹+1∙2⁰ = 0+0+8+0+0+1 = 9₁₀

Переведем 001001₂ в восьмеричную и шестнадцатеричную:

Получаем: 001001₂ = 9₁₆

9₁₀ = 11₈

Задание 3. Переведем целые числа из шестнадцатеричной системы счисления:

Переведем число 1A1B в десятичную систему:

1A1B₁₆ = 1∙16³+10∙16²+1∙16¹+11∙16⁰ = 4096+2560+16+11 = 6683₁₀

Переведем в восьмеричную и двоичную систему через десятичную (рисунок 8):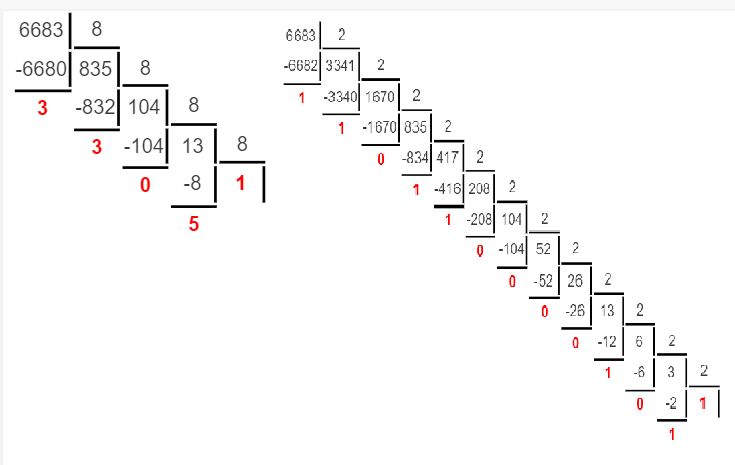



Рисунок 8 – перевод в восьмеричную и двоичную

Получаем: 1A1B₁₆ =6683₁₀ = 1101000011011₂

1A1B₁₆ =6683₁₀=15033₈

Переведем 2350₁₆ в десятичную :

2350₁₆ = 2∙16³+3∙16²+5∙16¹+0∙16⁰ = 8192+768+80+0 = 9040₁₀

Переведем 2350₁₆ в восьмеричную и двоичную (рисунок 9):

2350₁₆ =9040₁₀ = 21520₈

9040₁₀ = 10001101010000₂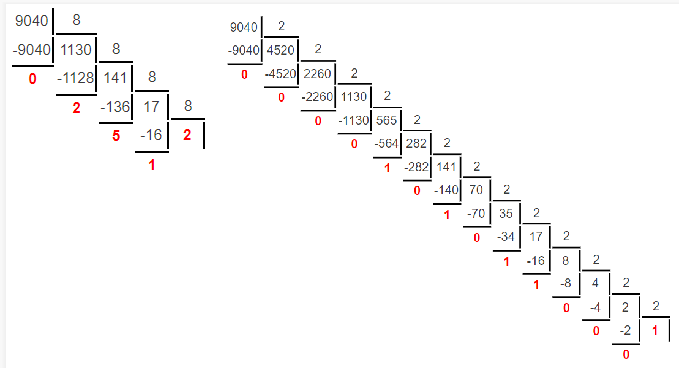



Рисунок 9 – перевод в восьмеричную и двоичную

Переведем 3239₁₆ в десятичную систему:

3239₁₆ = 3∙16³+2∙16²+3∙16¹+9∙16⁰ = 12288+512+48+9 = 12857₁₀

Переведем 3239₁₆ в восьмеричную и шестнадцатеричную через десятичную (рисунок 10):

Получим : 3239₁₆ = 12857₁₀ = 31071₈

3239₁₆ = 12857₁₀ = 11001000111001₂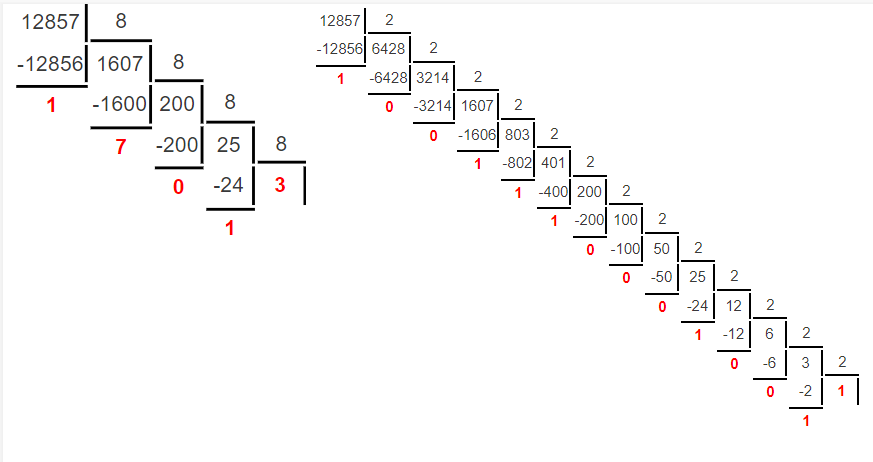



Рисунок 10 – перевод в восьмеричную и двоичную

Задание 4. Сложим числа двоичные числа 0110 + 1100 (рисунок 11):

Двоичные числа складываются так же, как и десятичные, то есть по разрядам. Сложение начинается с меньших разрядов. Оба числа пишут поразрядно друг над другом. В случае переноса разряда единица записывается в следующий разряд и учитывается при сложении цифр этого разряда. Иными словами при переносе разряда приходится складывать три двоичных числа.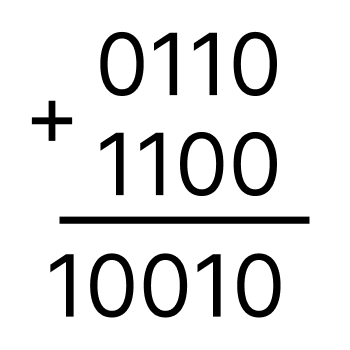

Рисунок 11 – сложение двоичных

Поучаем результат сложения - 10010₂

Произведем сложение восьмеричных чисел, оно аналогично сложению двоичных 274 + 235 (рисунок 12):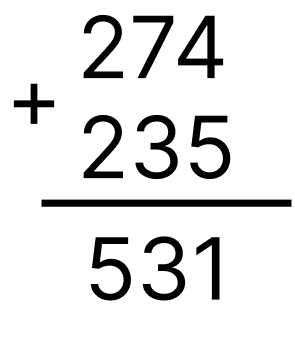

Рисунок 12 - сложение восьмеричных

Поучаем результат сложения -531₈

По такому же принципу сложим шестнадцатеричные числа 93 + 2C (рисунок 13):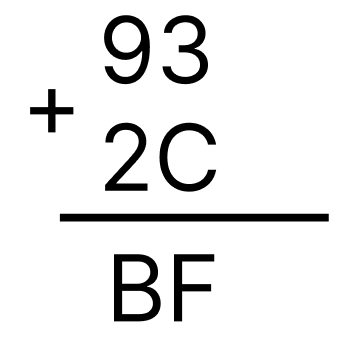



Рисунок 13- сложение шестнадцатеричных

Поучаем результат сложения -BF₁₆

Задание 5. Найдем разность двоичных чисел 1110 – 1100 (рисунок 14):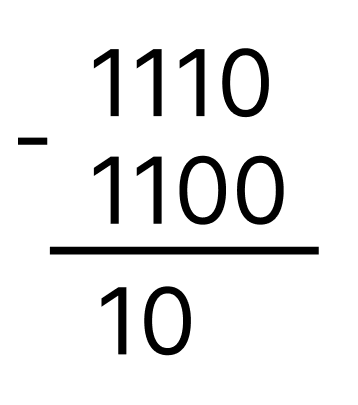

Рисунок 14 разность двоичных

В результате разности получаем - 10₂

Найдем разность восьмеричный 274 – 235 (рисунок 15) :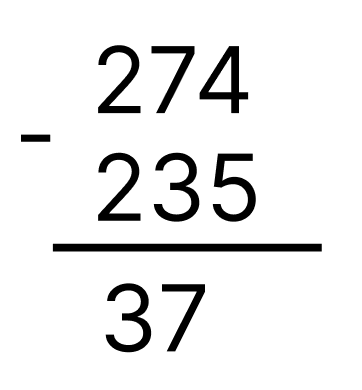

Рисунок 15 – разность восьмеричных

В результате разности получаем – 37₈

Найдем разность шестнадцатеричных 93 – 2C (рисунок 16):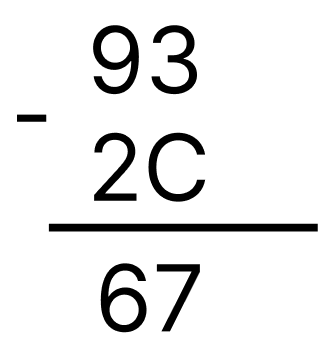

Рисунок 16- разность шестнад-х

В результате разности получаем – 67₁₆

Задание 6. Вычислим значение выражения и представить в десятичной системе счисления B1₁₆– 1011₂ * 117₈ (рисунок 17).Для этого приведем все значение к одному виду.117₈= 1001111_{2 ,} B1₁₆ =10110001₂

Контрольные вопросы

1. 
   Что называется системой счисления?
   

Система счисления - это символический метод записи чисел, представление чисел с помощью письменных знаков.

2. 
   Какие системы счисления называются непозиционными? Почему? Приведите пример такой системы счисления и записи чисел в ней.
   

Непозиционными являются нумерации, где положение цифры в числе (разряд) не влияет на её значение. К примеру Римская нотацию (IV,III и тд).

3. 
   Какие системы счисления применяются в вычислительной технике: позиционные или непозиционные? Почему
   

В вычислительной технике используются позиционные системы счисления, поскольку это связано с электронными схемами которые могу показывать всего 2 состояния 1 и 0. По этому для простоты кодировки и декодирования используют в основном двоичную систему счисления для передачи информации процессору и обратно. 

4. 
   Как изображается число в позиционной системе счисления?
   

Любое число в позиционной системе счисления изображается последовательностью цифр: Х = аn-1 an-2…a1a0. где aiє{0,1,…,q-1}, q – основание системы счисления.

5. 
   Что называется основанием системы счисления?
   

Основание системы счисления — это количество цифр в алфавите (мощность алфавита). 

6. 
   Как можно представить целое положительное число в позиционной системе счисления?
   

Любое число в позиционной системе счисления можно представить в развернутой и свернутой форме

7. 
   Какие системы счисления применяются в компьютере для представления информации?
   

В компьютере для представления информации используются десятичная, двоичная и шестнадцатеричная системы счисления.

8. По каким правилам выполняется сложение двух положительных целы

Правила сложения в любой позиционной системе счисления аналогичны правилам сложения в десятичной системе счисления. При сложении цифры суммируются по разрядам, и если при этом возникает избыток, то он переносится влево

9.Каковы правила выполнения арифметических операций в двоичной системе счисления?

Операция сложения выполняется так же, как и в десятичной системе. Переполнение разряда приводит к появлению единицы в следующем разряде

10. Для чего используется перевод чисел из одной системы счисления в другую?

Перевод в разные системы счисления является важной частью машинной арифметики.

11. Сформулируйте правила перевода чисел из системы счисления с основанием р в десятичную систему счисления и обратно: из десятичной системы счисления в систему счисления с основанием s. Приведите примеры.

Перевод из десятичной системы счисления в любую другую. Чтобы перевести целое положительное десятичное число в систему счисления с другим основанием, нужно это число разделить на основание. Полученное частное снова разделить на основание, и дальше до тех пор, пока частное не окажется меньше основания. В результате записать в одну строку последнее частное и все остатки, начиная с последнего. Пример : 10₁₀=1010₂

12. Как выполнить перевод чисел из двоичной системы счисления в восьмеричную систему и обратно? Из двоичной системы счисления в шестнадцатеричную систему и обратно? Приведите конкретные примеры

Для перевода можно перевести двоичное число в десятичное по формуле

A₂ = a_n-1 ∙ 2^n-1 + a_n-2 ∙ 2^n-2 + ∙∙∙ + a₀ ∙ 2⁰, или воспользоваться таблице перевода в восьмеричную. С шестнадцатеричную систему точно также .Пример 101010₂

= 52_8, 101010₂= 2А₁₆

13. По каким правилам выполняется перевод чисел из восьмеричной в шестнадцатеричную систему счисления и наоборот?

Перевод возможен через десятичную систему или через таблицу. К примеру

10101010₈ =208208₁₆

Вывод: При работе над лабораторной я изучила позиционные системы счисления и провела арифметические действия над ними.