лаба по основам теории управления. оту, лр1, ключников, богатова. Отчет по лабораторной работе 1 по дисциплине Основы теории управления
 Скачать 0.91 Mb. Скачать 0.91 Mb.
|
|
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ ФЕДЕРАЛЬНОЕ государственное БЮДЖЕТНОЕ образовательное учреждение высшего образования «НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ» __________________________________________________________________ Кафедра вычислительной техники  ОТЧЕТ По лабораторной работе №1 по дисциплине: «Основы теории управления» Вариант № 7
Новосибирск 2022 Цель работы Исследовать динамические характеристики типовых звеньев систем автоматического управления (САУ), а также познакомиться с представлениемтиповых звеньев структурными схемами. При выполнении лабораторных работ используется пакет программ Matlab/Simulink. Основная часть 2.1 Исходные данные Таблица 1. Исходные данные
2.2 Основные сведения Интегрирующее звено выполняет операцию интегрирования входного сигнала и его уравнение можно записать в виде y(t) = y(0) + k 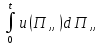 , ,где y - выходная переменная звена; u - входное воздействие; k- коэффициент передачи звена; y(0) - начальные условия, y(0) const. Дифференцируя данное уравнение, получим соотношение в виде дифференциального уравнения первого порядка ẏ = ku. Передаточная функция интегрирующего звена имеет вид: W(s) = 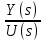 = = 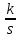 . .Апериодическое звено описывается дифференциальным уравнением T ẏ + y = ku, где T - постоянная времени, k - коэффициент передачи. Передаточная функция апериодического звена имеет вид: W(s) = 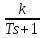 . .Звено второго порядка описывается дифференциальным уравнением T2ÿ +2dTẏ + y = ku, где d - коэффициент демпфирования. Передаточная функция звена имеет вид: W(s) = 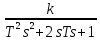 . .При d 0 получаем консервативное звено, при 0 Идеальное дифференцирующее звено описывается уравнением y = ku̇, которое не может быть реализовано на практике. Дифференциальное уравнение реального дифференцирующего звена имеет следующий вид: μẏ + y = ku̇, а его передаточная функция: W(s) = 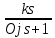 . .2.3 Ход работы 2.3.1 Модель интегрирующего звена Переходная функция (ПФ)  Рис. 1 - Структурная схема интегрирующего звена 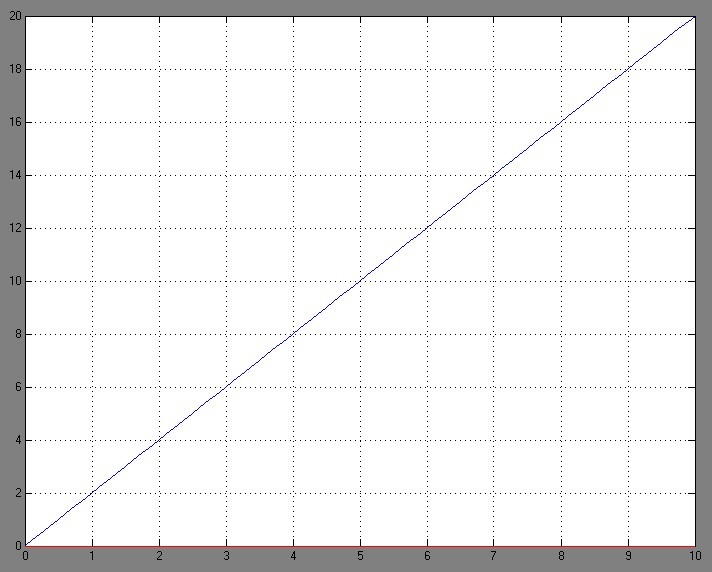 Рис. 2 - График переходной функции интегрирующего звена Импульсная переходная функция (ИПФ) 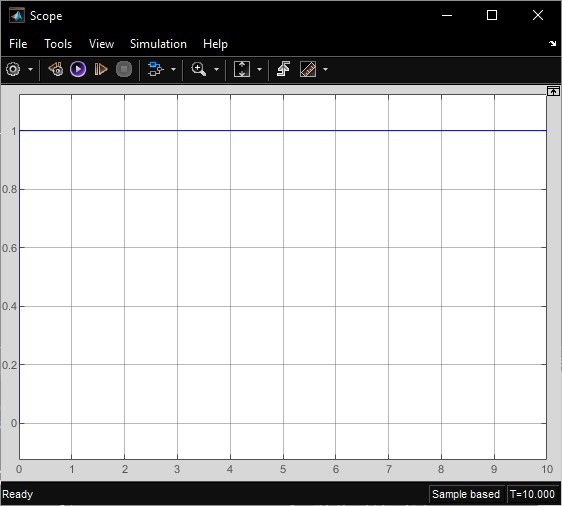 Рис. 3 - График импульсной переходной функции интегрирующего звена 2.3.3 Увеличивая и уменьшая k интегрирующего звена в два раза оценить его влияние на вид ПФ и ИПФ. ПФ 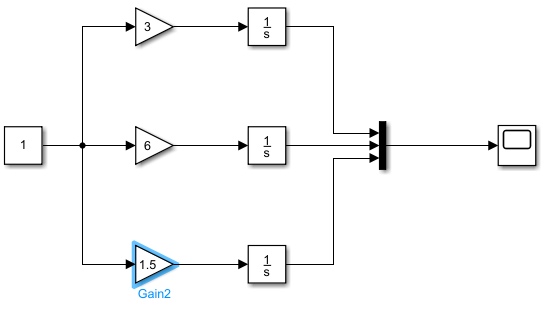 Рис. 7 - Структурная схема интегрирующего звена для переходной функции с изменяемым k 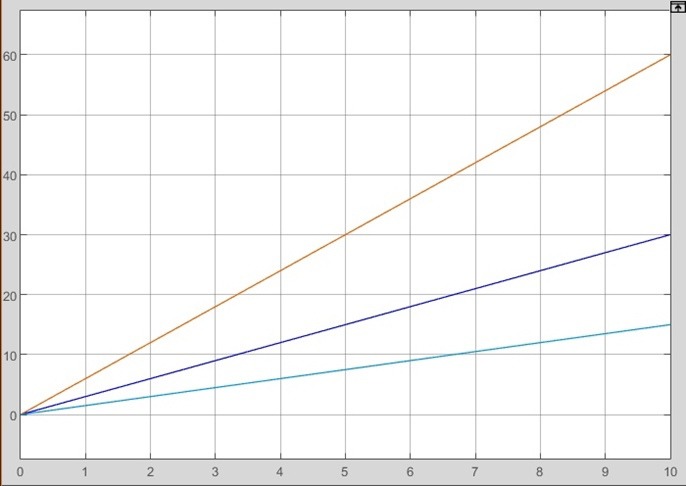 Рис. 8 - Графики переходной функции интегрирующего звена при изменяемом k, фиолетовый – k/2 = 1.5, синий – k = 3, зеленый – 2k = 6 Вывод: Из графика видно, что чем больше коэффициент передачи звена (k), тем быстрее возрастает график переходной функции. ИПФ 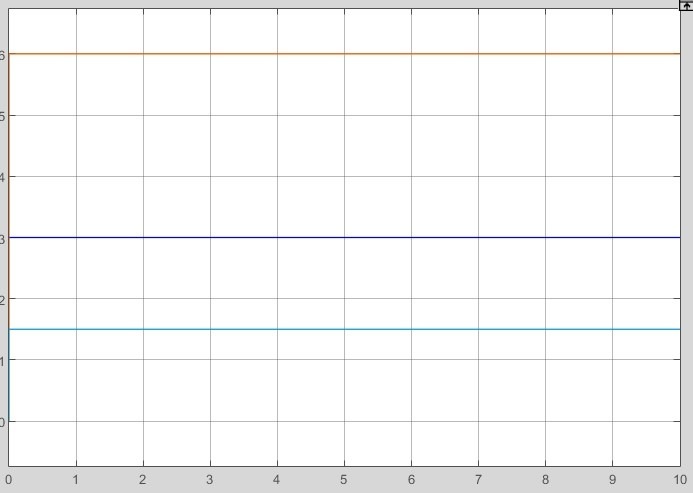 Рис. 9. Графики импульсной переходной функции при изменяемом k, где фиолетовый – k/2 = 1.5, синий – k = 3, зеленый – 2k = 6 Вывод. Из графика видно, что импульсная переходная функция описывается уравнением w(t) = k, следовательно, чем больше k, тем выше будет располагаться прямая на графике. Эксперименты аналогично п. 4.1 выполнить для апериодического звена ПФ  Рис. 10. Структурная схема звена для апериодического звена 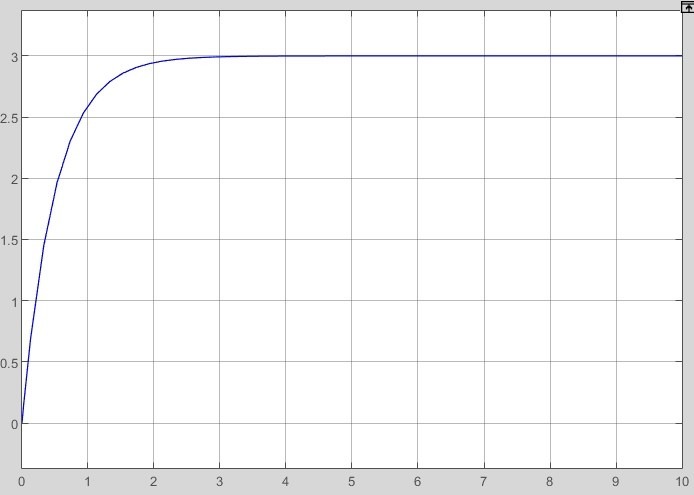 Рис. 11. График переходной функции для апериодического звена ИПФ 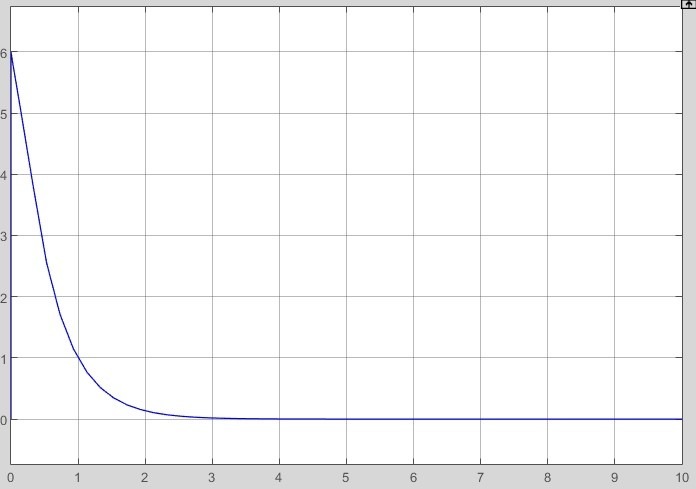 Рис 12. График импульсной переходной функции для апериодического звена 2.3.5 Изменяя последовательно k и T апериодического звена, оценить их влияние на вид ПФ. Изменяем k 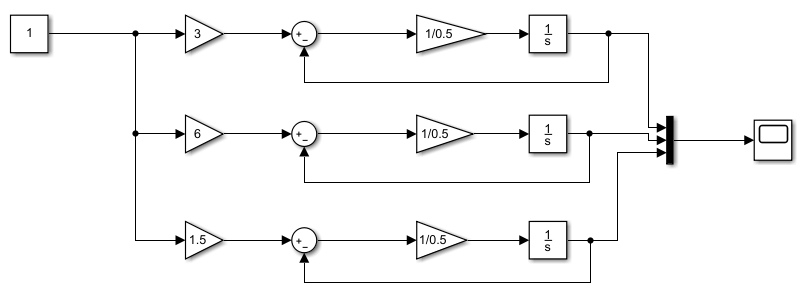 Рис. 13. Структурная схема апериодического звена для переходной функции с изменяемым k 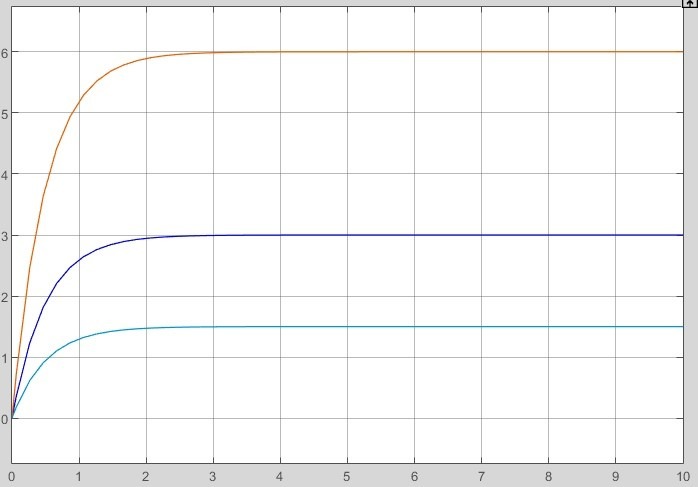 Рис. 14. График переходной функции при изменяемом k, где фиолетовый – k/2 = 1.5, синий – k = 3, зеленый – 2k = 6 Вывод: Из графика видно, что при изменении k меняется верхняя граница переходной функции, чем больше k, тем выше верхняя граница. А) При увеличении коэффициента передачи k в 2 раза переходная функция начинает расти в 2 раза быстрее Б) При уменьшении k – функция растёт медленнее с более пологим графиком, то есть переходной процесс длится дольше. Изменяем T 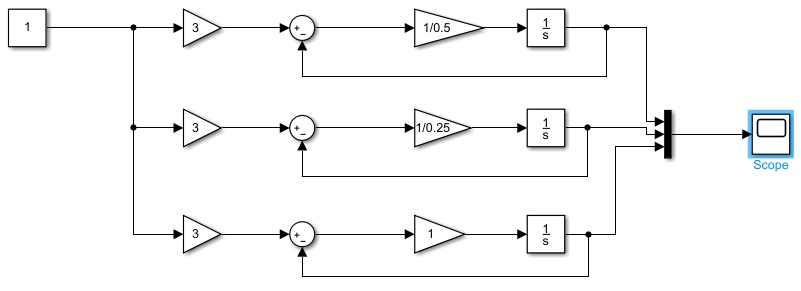 Рис. 15. Структурная схема апериодического звена для переходной функции с изменяемым Т 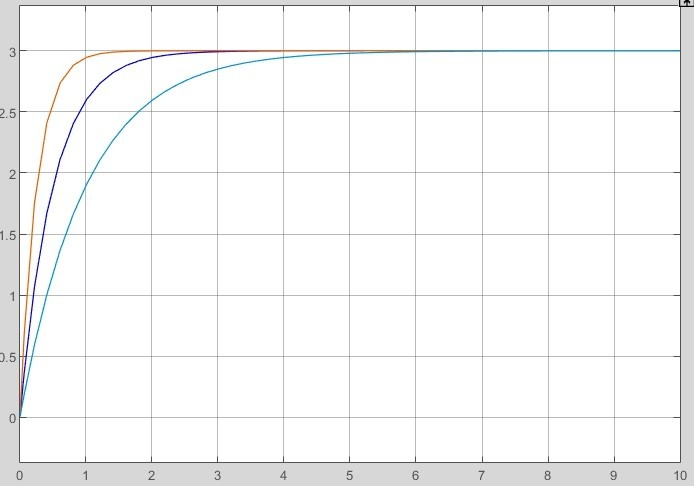 Рис. 16. График переходной функции при изменяемом Т, где фиолетовый – k/2 = 1.5, синий – k = 3, зеленый – 2k = 6 Вывод: Из графика видно, что при изменении T, верхняя граница не меняется (все функции стремятся к 3), но меняется скорость приближения к этой границе. Чем больше T, тем быстрее функция достигает верхней границы. А) При увеличении постоянной времени T в 2 раза переходная функция начинает расти в 2 раза медленнее Б) При уменьшении T – функция растёт быстрее с более крутым графиком, то есть переходной процесс происходит быстрее. 2.3.6 Эксперименты аналогично п. 4.1 выполнить для колебательного звена ПФ 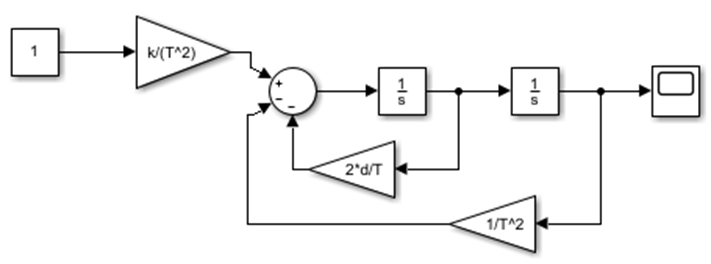 Рис. 17. Структурная схема колебательного звена для переходной функции 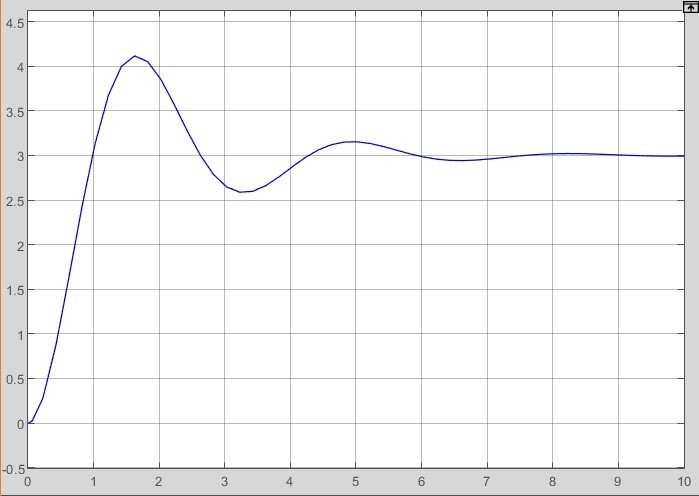 Рис. 18. График переходной функцииколебательного звена ИПФ 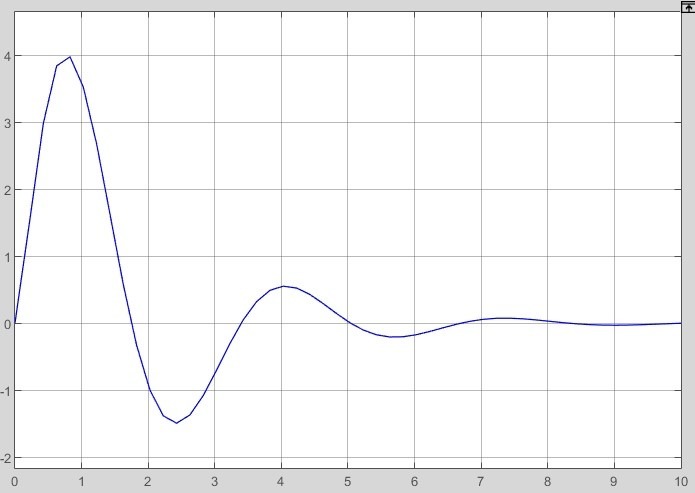 Рис 19. График импульсной переходной функции колебательного звена 2.3.7 Изменяя последовательно k, T, d, оценить их влияние на переходную характеристику колебательного звена. Изменяем k 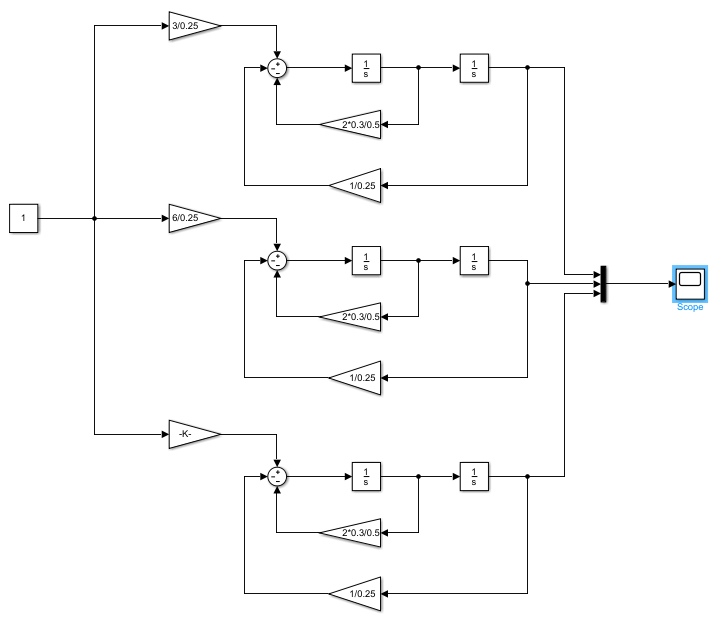 Рис. 20. Структурная схема колебательного звена для переходной функции с изменяемым k Рис. 20. Структурная схема колебательного звена для переходной функции с изменяемым k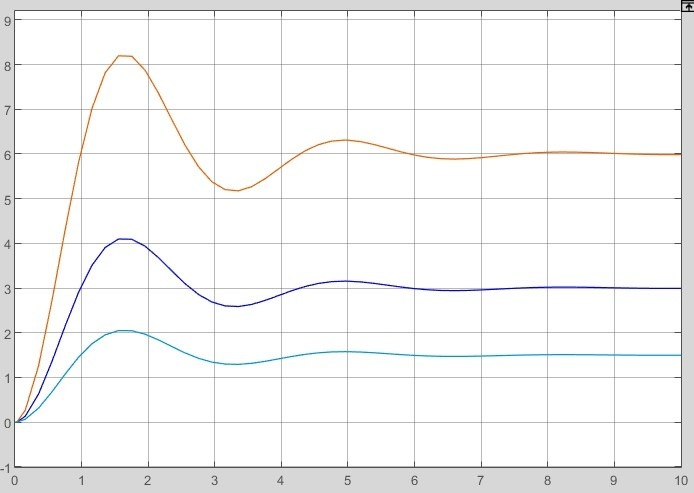 Рис. 21. График переходной функции при изменяемом k, где фиолетовый – k/2 = 1.5, синий – k = 3, зеленый – 2k = 6 Вывод: Из графика видно, что изменение k влияет только на масштаб, то есть чем больше k, тем выше поднимется функция. Графики симметричны друг другу и различаются только масштабом. 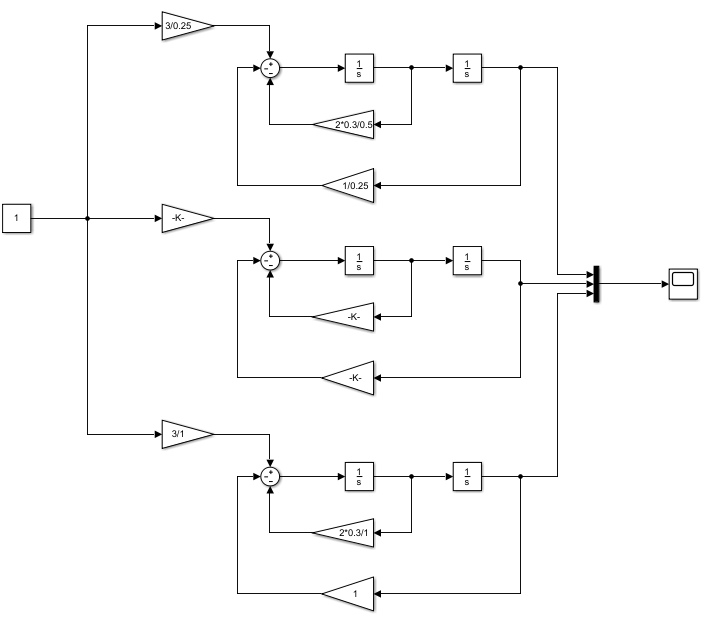 Рис. 22. Структурная схема колебательного звена для переходной функции с изменяемым T 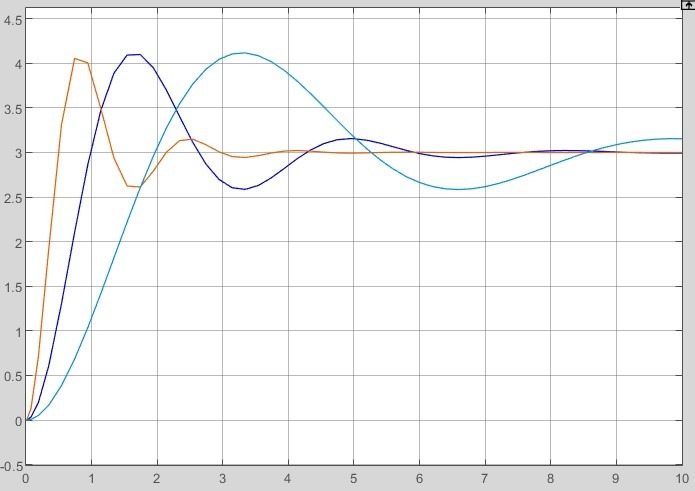 Рис. 23. График переходной функции при изменяемом Т, где зеленый – T/2 , синий – T , фиолетовый – 2T Вывод: Из графика видно, что чем больше T, тем сильнее он влияет на график функции. Изменяем d 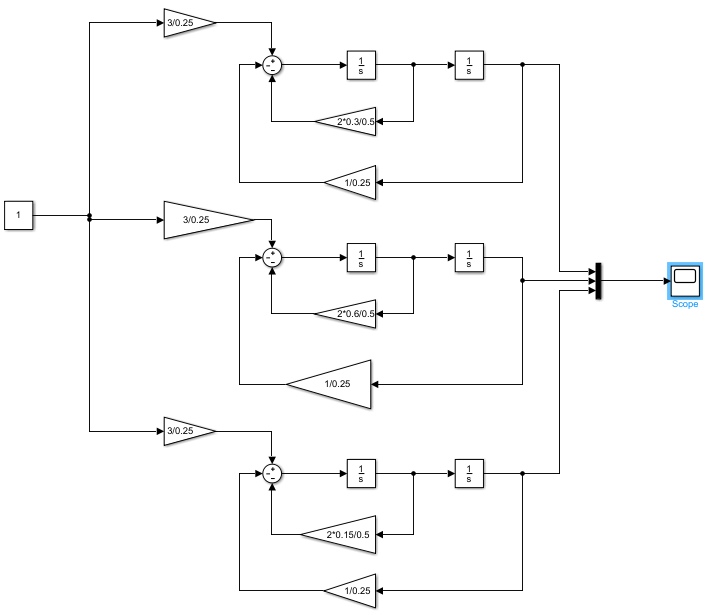 Рис 24. Структурная схема колебательного звена для переходной функции с изменяемым d 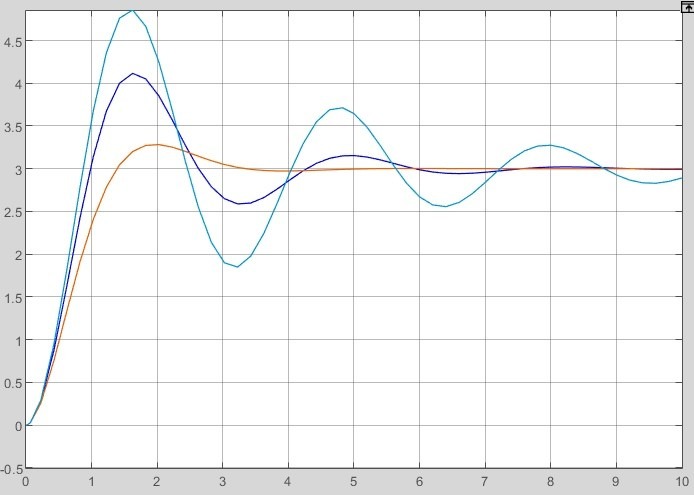 Рис 25. График переходной функции при изменяемом d, где фиолетовый – d/2, синий – d, зеленый – 2d Вывод. Из графика видно, что изменение d, приводит к изменению вида кривой. При малой d график напоминает затухающие колебания, при больших d – возрастающую функцию, стремящуюся к константе 3. 2.3.8 Исследовать характеристики реального дифференцирующего звена аналогично п.4.1. ПФ 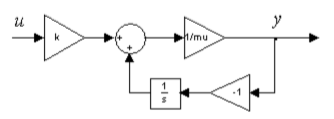 Рис 26. Структурная схема реального дифференцирующего звена для переходной функции 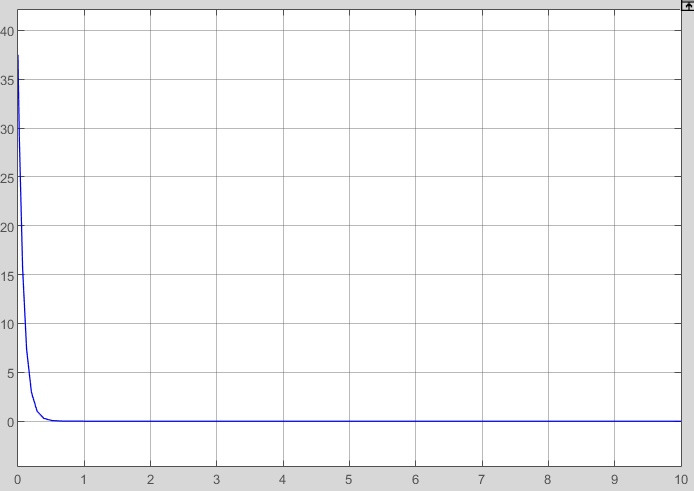 Рис 27. График переходной функции для реального дифференцирующего звена ИПФ 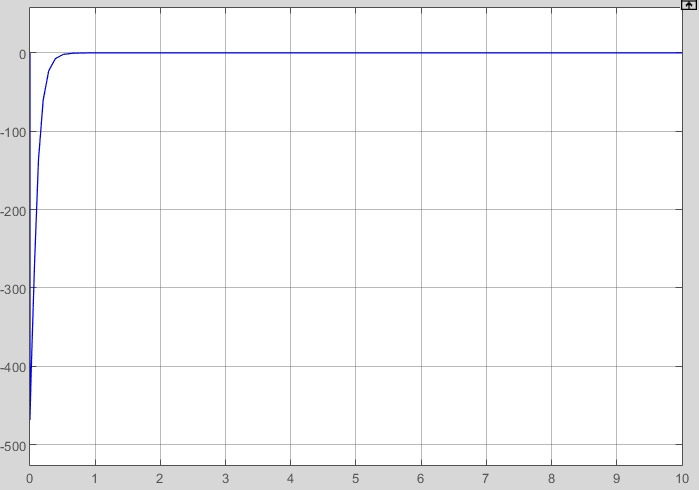 Рис 28. График импульсной переходной функции для реального дифференцирующего звена 2.3.9 На вход реального дифференцирующего звена подать выходной сигнал колебательного звена. Сравнить выходной сигнал реального дифференцирующего звена с сигналом для точного значения производной. Оценить влияние на точность воспроизведения производной. 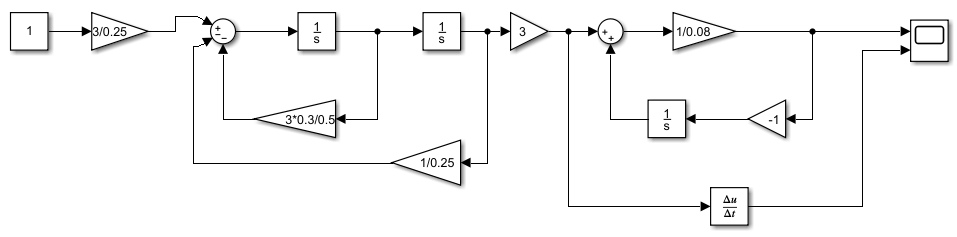 Рис 29. Структурная схема колебательного звена для переходной функции с изменяемым d ПФ 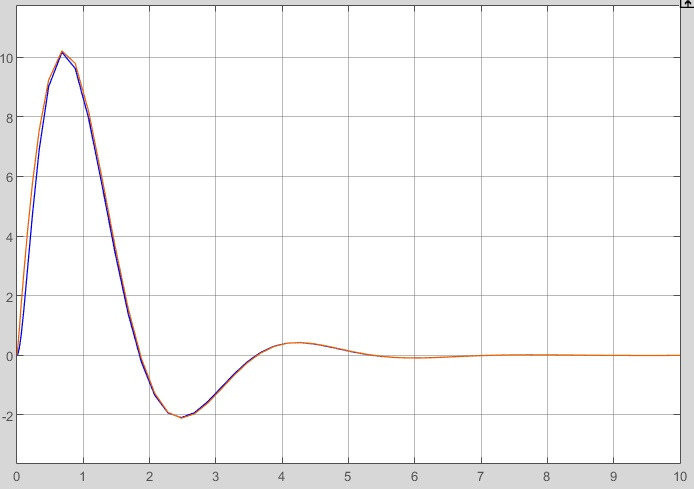 Рис 30. График переходной функции. Синий – реальное дифференцирующее звено, зеленый – точное значение производной. Вывод: Из графиков видно, что выходной сигнал реального дифференцирующего звена и точного значения производной практически совпадают. Влияние на точность воспроизведения производной. 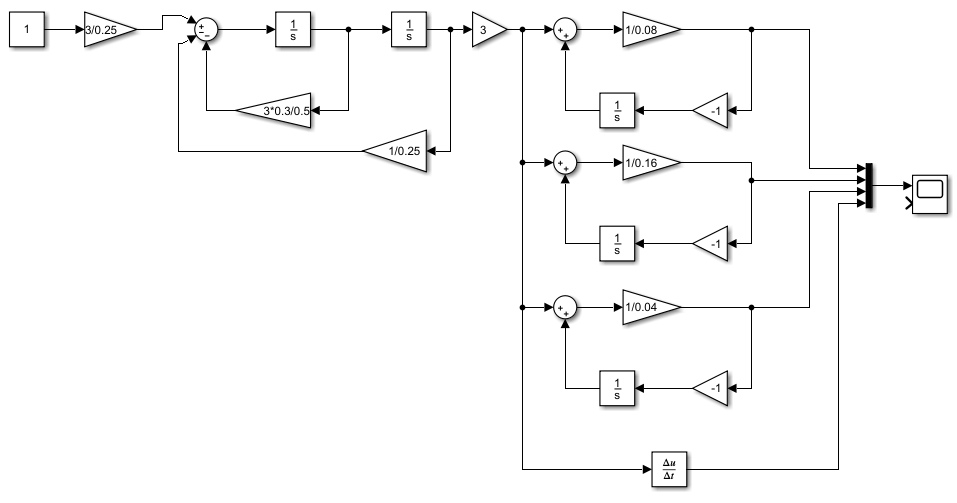 Рис 31. Структурная схема колебательного звена для переходной функции с изменяемым d 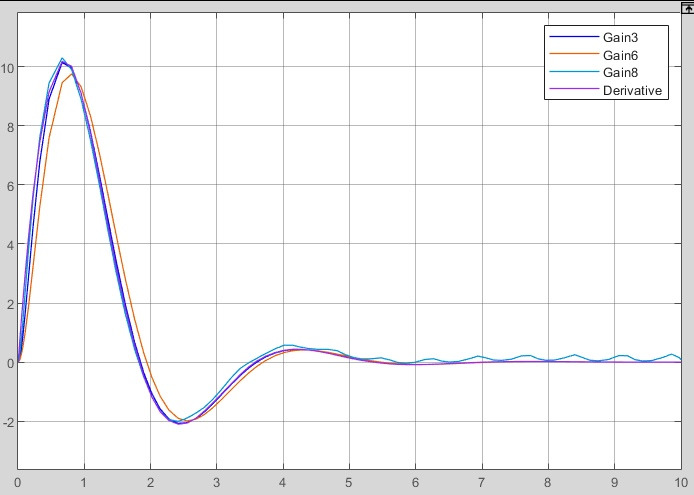 Рис 32. График переходной функции. Синий – μ = 1/0.16, зеленый – μ = 1/0.08, бирюзовый – μ = 1/0.04, фиолетовый – точное значение производной. Вывод: Из графика видно, что, чем меньше , тем ближе к точному значению. Выводы Полученные экспериментальным путём семейства переходных функций для интегрирующего, апериодического и реального дифференцирующего звеньев сходятся с теоретическими. Амплитудно-частотная и фазо-частотная характеристики также сошлись с теоретически ожидаемым. АЧХ показывает, что звено пропускает сигнал тем сильнее, чем меньше его частота. При 𝜔=0 модуль частотной передаточной функции стремится к бесконечности, а при 𝜔→∞ 𝐴(𝜔)→0. |
