ЛР 1 для ТОЭ. ЛР 1 для ТОЭ нов. Отчет по лабораторной работе 1 По дисциплине тоэ
 Скачать 158.63 Kb. Скачать 158.63 Kb.
|
|
Некоммерческое акционерное общество «АЛМАТИНСКИЙ УНИВЕРСИТЕТ ЭНЕРГЕТИКИ И СВЯЗИ» имени Гумарбека Даукеева Кафедра электротехники ОТЧЕТ по лабораторной работе № 1 По дисциплине ТОЭ На тему Исследование цепи постоянного тока Образовательная программа 6B07108 – «Автоматизация и управление» Выполнил Архиреев Н.А. Группа АУ-21-8 (Ф.И.О. студента) Проверила Старший преподаватель Креслина С.Ю (Ученая степень, звание, Ф.И.О. преподавателя) __________ ________________ «____» сентябрь 2022г. (оценка) (подпись) Алматы 2022 Лабораторная работа № 1. Исследование цепи постоянного токаЦель работы: приобрести навыки сборки электрических цепей и работы с измерительными приборами, а также проверить на практике основные законы и методы расчета электрических цепей постоянного тока. Порядок выполнения работыВыбрать два резистора с разной величиной сопротивлений R1 и R2 в диапазоне от 50 до 300 Ом. Собрать цепь по схеме рисунок 1.1.Изменяя напряжение на входе цепи от 0 до 20 В снять показания вольтметра и амперметра, то есть ВАХ, для каждого из выбранных резисторов. Результаты измерений записать в таблицу 1.1.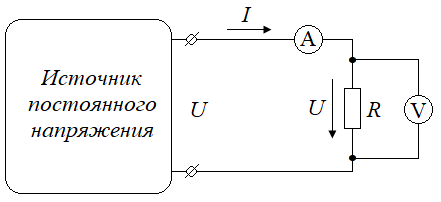 Таблица 1.1 – ВАХ резисторов
Выбрать пять резисторов с разными сопротивлениями в диапазоне от 50 Ом до 300 Ом. Измерить фактические значения резисторов и записать в таблицу 1.2. Собрать цепь по одной из схем, представленных на рисунке 1.2. Установить величину ЭДС источников постоянного напряжения разной величины в диапазоне от 5 до 20 В.Таблица 1.2 – Фактические значения резисторов
Выбрать произвольно и указать направления токов в ветвях схемы. Амперметр и вольтметр включать в соответствии с выбранным направлением тока, так чтобы ток протекал через прибор от плюса к минусу. Измерить токи во всех ветвях и напряжения на всех элементах цепи. Если прибор показывает отрицательное значение, можно записать показание с минусом или изменить направление тока на противоположное и записать показание прибора с плюсом. Показания приборов записать в таблицу 1.3, в строку «Эксперимент».Таблица 1.3 – Токи в ветвях и напряжения на элементах цепи
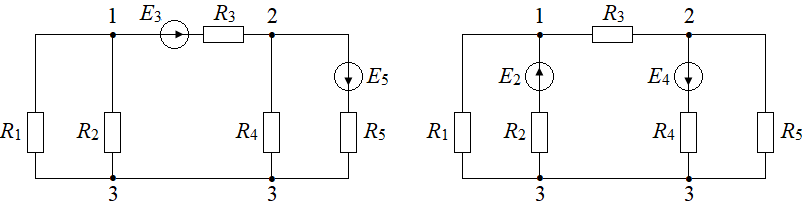 Вариант 3 Вариант 4 Рисунок 1.2 – Варианты схем цепей постоянного тока Анализ результатов экспериментаПо результатам таблицы 1.1 построить на одном рисунке ВАХ обоих резисторов. Убедиться, что полученные графики являются прямыми линиями, что свидетельствует о линейности резисторов. Сравнить характеристики двух резисторов и убедиться в том, что сопротивление резистора пропорционально тангенсу угла наклона ВАХ к оси тока.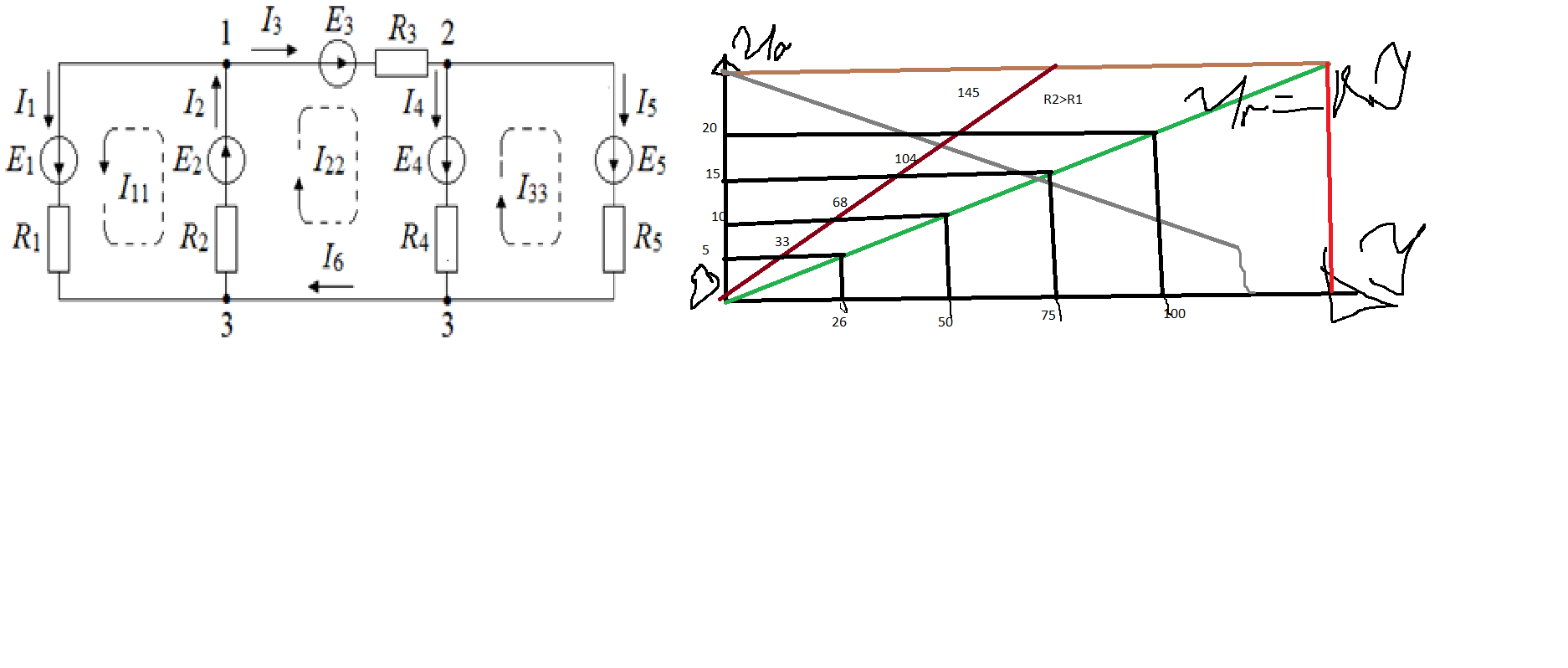 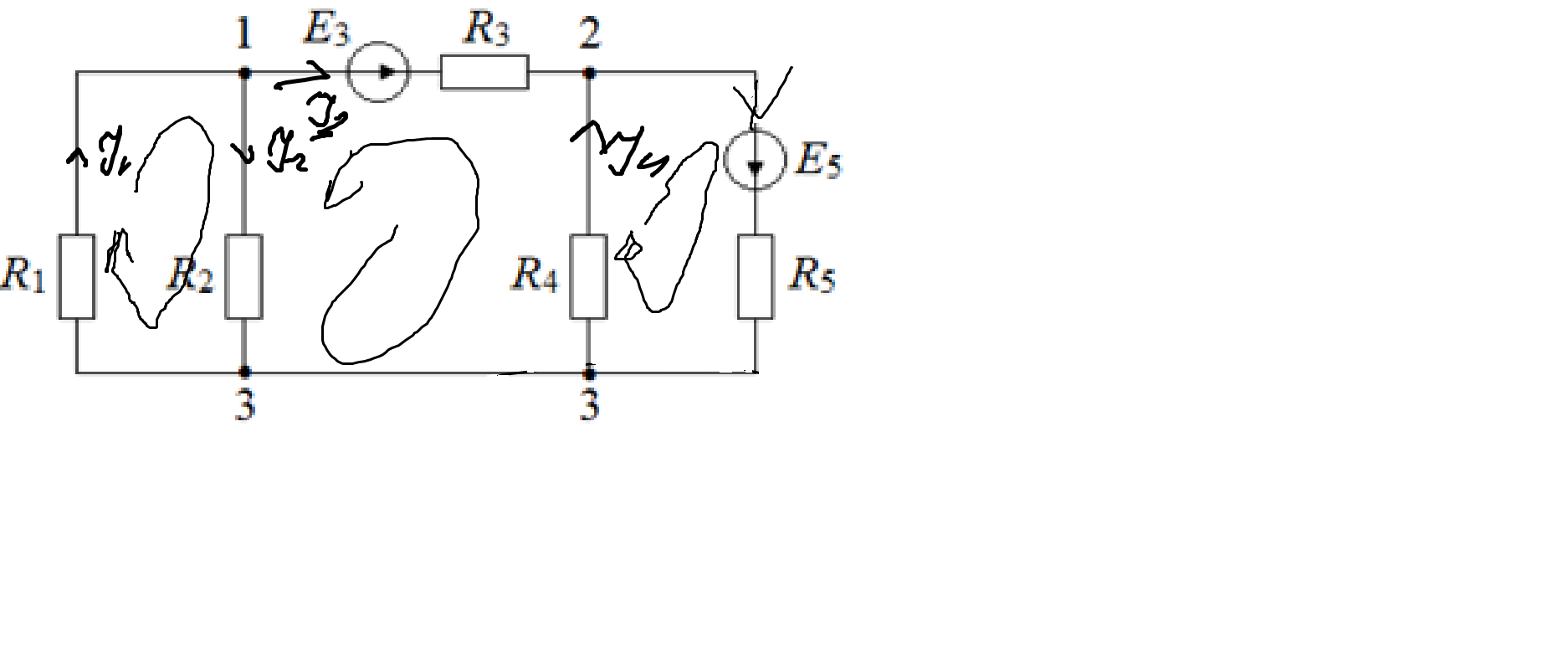 Составить систему уравнений для расчёта токов в ветвях схемы тремя способами:по законам Кирхгофа; методом контурных токов (МКТ); методом узловых потенциалов (МУП). Рассчитать токи одним из методов: МКТ или МУП. Рассчитать напряжения на всех резисторах. Результаты записать в таблицу 1.3 в строку «Расчет». Сравнить результаты расчёта и эксперимента. Сделать вывод о подтверждении теории на практике, а также о преимуществах и недостатках расчёта по сравнению с экспериментом.Методические указанияКоличество уравнений, записываемых по первому закону Кирхгофа равно числу узлов схемы минус один: nI зК = nузлов – 1.Количество уравнений, записываемых по второму закону Кирхгофа равно числу ветвей схемы с неизвестными токами минус количество уравнений по первому закону Кирхгофа: nII зК = nветвей – nJ – nIзК = nветвей – nJ – nузлов + 1, где nJ – число ветвей с идеальными источниками тока J.Найденное число уравнений nII зК равно числу независимых контуров в схеме. Контур является независимым, если он содержит хотя бы одну собственную ветвь, не входящую ни в один из других контуров. МКТ позволяет сократить число уравнений решаемых в системе до числа уравнений по второму закону Кирхгофа, а МУП – до числа уравнений по первому закону Кирхгофа. Результаты расчёта МКТ нельзя проверять, подстановкой в уравнения по первому закону Кирхгофа. Для проверки результатов расчёта МКТ надо их подставить в уравнения по второму закону Кирхгофа, или подстановкой в уравнение баланса мощностей схемы. Результаты расчёта МУП нельзя проверять, подстановкой в уравнения по второму закону Кирхгофа. Для проверки результатов расчёта МУП надо их подставить в уравнения по первому закону Кирхгофа, или подстановкой в уравнение баланса мощностей схемы. Уравнение баланса мощностей схемы можно использовать как универсальный способ проверки результатов расчёта любым методом. Рассмотрим пример расчёта токов в ветвях разветвлённой цепи постоянного тока, схема которой представлена на рисунке 1.3. 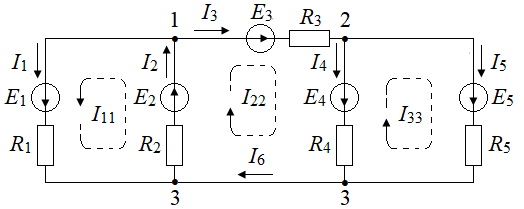 Рисунок 1.3 – Схема разветвлённой цепи постоянного тока Исходные данные: E3 = 19,5В,E5 = 20,7 В, R1 = 75 Ом, R2 = 150 Ом,R3 = 200 Ом,R4 = 150 Ом,R5 = 75 Ом. Выберем произвольно направления токов в ветвях цепи (рисунок 1.3). Токи в третьей и шестой ветвях одинаковые, что следует из первого закона Кирхгофа, который справедлив не только для любого узла, но также и для любого сечения схемы. Неизвестных токов – пять, поэтому система уравнений по законам Кирхгофа будет состоять из пяти уравнений, два из которых составлены по первому закону и три – по второму:
Выберем произвольно направления токов в ветвях цепи (рисунок 1.3). Токи в третьей и шестой ветвях одинаковые, что следует из первого закона Кирхгофа, который справедлив не только для любого узла, но также и для любого сечения схемы. Неизвестных токов – пять, поэтому система уравнений по законам Кирхгофа будет состоять из пяти уравнений, два из которых составлены по первому закону и три – по второму: I1-I2-I3=0 I3+I4-I5=0 R1I1-R2I2=E1+E2 R2I2-R3I3+R4I4=E2+E3+E4 R4I4+R5I5=E4+E5 Система уравнений по методу контурных токов: I11=(R1+R2)+I22R2+0=0 I22(R2+R3+R4)+I11R2+0+I33R4=-E3 I33(R4+R5)+I22R4+0=E5 Результаты расчёта МКТ: I11=(R1+R2)+I22R2+0=0 I22(R2+R3+R4)+I11R2+0+I33R4=-E3 I33(R4+R5)+I22R4+0=E5 I1=I11 I2=I11+I22 I3=-I22 I4=I22+I33 I5=I33 I3=I6=-I22 Система уравнений по методу узловых потенциалов, примем φ3 = 0: G2=G3=G4=G5=1/2=0,5 f1(g1+g2+g3)-f2g3=-E3g3 f2(g3+g4+g6)-f1g3=E3g3-E5g5 I1=(f3-f1)/R1=(f3-f1)g1=-2 I2=(f1-f3)/R2=(f1-f3)g2= 1 I3=(f1-f2+E3)/R3=(f1-f2+E3)g3= 0,01 I4=(f3-f2)/R4=(f3-f2)g4= -1 I5=(f2-f3+E5)/R5=(f2-f3+E5)/R5=2,28 I6=I3=0,01 Вывод: Главным выводом первой лабораторной работы, является подтверждение двух тезисов, выдвигаемых законами Кирхгофа. А именно, первый закон Кирхгофа, утверждающий, что алгебраическая сумма токов ветвей, сходящихся в каждом узле любой цепи, равняется нулю. На практике мы это проверили, составив цепь из 5 резисторов, далее определив с помощью мультиметра фактические значения резисторов и силы тока в цепи, а также значения ЭДС. Алгебраическая сумма напряжений на резистивных элементах замкнутого контура равна алгебраической сумме ЭДС, входящих в этот контур. Однако если же в контуре нет ЭДС, то суммарное падение напряжений равно нулю. На уравнения первого и второго закона Кирхгофа опираются метод контурных токов и метод узловых потенциалов. За время работы была также составлена ВАХ, характеризующая изменение силы тока в зависимости от изменения напряжения и основывающаяся на законе Ома. Именно по первому и второму законам Кирхгофа было составлено первые пять уравнений расчетной части. Опираясь на эти уравнения, был произведен расчет по методу узловых потенциалов. |
