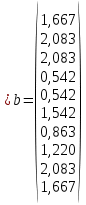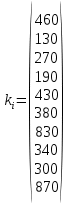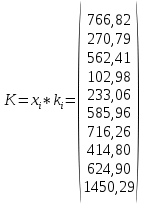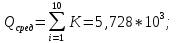Контрольная. 1 Бочаров. Отчет по лабораторной работе 1 по теме
 Скачать 59.52 Kb. Скачать 59.52 Kb.
|
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИФГАОУ ВО «Крымский федеральный университет имени В. И. Вернадского» Физико-технический институт Кафедра компьютерной инженерии и моделирования Отчет по лабораторной работе №1 по теме: “Методика расчета трудоемкости выполнения алгоритма” по дисциплине "Компьютерные системы" Выполнил студент 4 курса Группы ИВТ-б-з-181(1) Бочаров Ю.Е Проверила: Руденко М.А. Симферополь, 2022 Цель: Научиться рассчитывать трудоемкость выполнения алгоритма двумя методами (сетевым и с помощью Марковских цепей). Теоретическая часть: Под трудоемкостью алгоритма понимается количество вычислительной работы, требуемой для его реализации. Трудоемкость характеризует затраты времени для реализации алгоритма на некоторой совокупности технических средств. Обычно трудоемкость оценивается количеством процессорных операций и операций ввода-вывода. Трудоемкость алгоритма является в общем случае случайной величиной и зависит от исходных данных. Поэтому трудоемкость алгоритма может быть определена только приближенно в терминах теории вероятности: математическими ожиданиями, дисперсией и т.д. В задачах оценки трудоемкости операторы алгоритма разделяют на функциональные, перехода и ввода-вывода. Совокупность операторов и связей между ними наиболее наглядно представляется графом алгоритма, где вершины соответствуют основным операторам алгоритма, а дуги отображают связи между операторами. Вершины графа бывают трех типов: начальная, конечная и операторная. Начальная вершина определяет начало алгоритма. Эта вершина не имеет ни одного входа и имеет только один выход. Конечная вершина определяет конец алгоритма и имеет не менее одного входа и ни одного выхода. Операторная вершина соответствует основному оператору или оператору ввода-вывода. Если она представляет функциональный оператор или ввода-вывода, то может иметь не меньше одного входа и только один выход. Если она представляет оператор перехода, то может иметь не меньше одного входа и не меньше двух выходов. Исходные данные для 30 варианта: 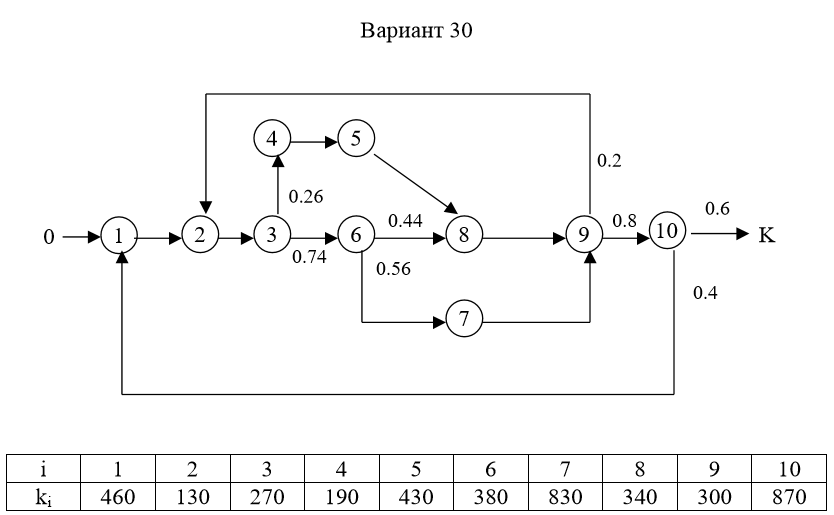 Рисунок 1 Граф алгоритма и таблица значений ki Выполнение работы: Первый метод (Марковские цепи) Линейные уравнения переходов, полученные по графу: 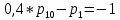 ; ;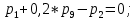 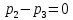 ; ;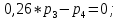 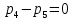 ; ;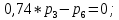 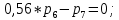 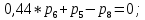 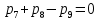 ; ;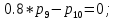
Второй метод определения трудоемкости (сетевой) Найдем коэффициенты для циклов: 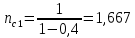 ; ; 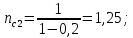 Общий вид уравнения для вычисления средней трудоемкости: 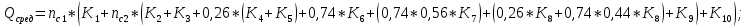 Подставляем в уравнение значения: Qсред= 1,667 * (460 + 1,25 * (130 + 270 + 0,26 * (190 + 430) + 0,74 * 380 + (0, 74 * 0,56 * 830) + (0,26 * 340 + 0,74 * 0,44 * 340) + 300) + 870); 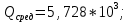 Найдем минимальную трудоемкость: 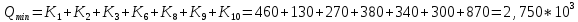 ; ;Теперь найдем максимальную трудоемкость выполнения алгоритма: Пусть: 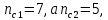 тогда: тогда: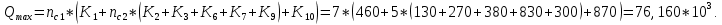 Вывод: В ходе выполнения лабораторной работы мы ознакомились с двумя методами определения трудоемкости алгоритма: с помощью Марковских цепей и сетевого метода оценки, закрепили полученные знания на практике. Анализ результатов показал, что значительной разницы между полученными значениями Qсред нет (5728 и 5728), что является показателем верно выполненной работы. С помощью сетевого метода были найдены значения минимальной и максимальной трудоемкости (Qmin=2750, Qmax=76160), составлен отчет о проделанной работе. | ||||||

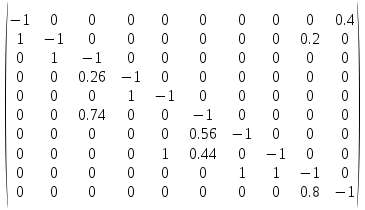 b=
b=