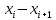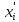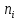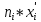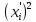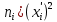Мат статистика Выборка. Отчет по лабораторной работе 1 Статистическое распределение и числовые характеристики выборки

• Название: Отчет по лабораторной работе 1 Статистическое распределение и числовые характеристики выборки
• Анкор: Мат статистика Выборка
• Дата: 24.06.2022
• Размер: 97.74 Kb.
• Имя файла: LR1_Moiseev.docx
• Тип: Отчет; #613389

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

Федеральное государственное автономное образовательное учреждение высшего образования

«Дальневосточный федеральный университет»


ПОЛИТЕХНИЧЕСКИЙ ИНСТИТУТ
Департамент нефтегазовых технологий и нефтехимии

ТЕОРИЯ ВЕРОЯТНОСТЕЙ И МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
ОТЧЕТ

по лабораторной работе №1

«Статистическое распределение и числовые характеристики выборки»

Выполнил студент гр. Б3120-21.03.01эоотх (1) ___________ С.А.Моисеев

Проверил к.т.н. ___________ П.Н.Французова _______________________ (оценка) «___» _____________________2022г.

Владивосток

2022

Статистическое распределение выборки

1. 
   Располагаем значения результатов эксперимента в неубывающем порядке, то есть записываем вариационный ряд:
   

57	57,3	57,7	58	58,1	59,3	59,5	59,9	60,1	60,7
61,3	61,9	62,1	62,3	62,5	62,7	62,9	63,1	63,5	63,7
64	64,4	64,8	64,9	65	65,2	65,6	65,8	66,1	66,3
66,7	66,9	67,1	67,3	67,4	67,8	68,5	68,7	68,9	69,1
69,3	69,4	69,5	69,6	70	70,6	70,8	70,9	71,1	71,2
71,3	71,4	71,5	71,6	71,7	71,8	71,9	72,1	72,5	72,6
72,8	72,9	73	73,5	73,8	74,1	74,3	74,7	74,8	74,9
75,1	75,3	75,4	75,5	76,1	76,8	77,1	77,3	77,6	77,7
77,9	78,1	78,3	78,7	78,9	79,1	80,4	80,5	80,6	80,7
80,7	80,8	81,1	81,3	82,3	82,4	83,1	83,7	83,9	84

2. 
   Находим медиану 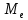вариационного ряда, то есть находим варианту, которая делит вариационный ряд на две части, равные по числу вариант
   

3. 
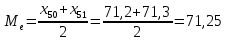   Находим моду 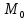вариационного ряда, то есть варианту, имеющую наибольшую частоту: 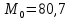. Данный вариационный ряд имеет одну моду.
   

4. 
   Находим по формуле размах варьирования .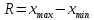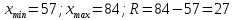
   

Вычисляем длину интервала по формуле: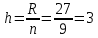



Все вычисления записываем в таблицу

mi	Границы интервалов	Середина интервала	Частота интервала	Относительная частота	Плотность частоты
1	57,00-60,00	58,50	8	0,080	0,0267
2	60,00-63,00	61,50	9	0,090	0,0300
3	63,00-66,00	64,50	11	0,110	0,0367
4	66,00-69,00	67,50	11	0,110	0,0367
5	69,00-72,00	70,50	18	0,180	0,0600
6	72,00-75,00	73,50	13	0,130	0,0433
7	75,00-78,00	76,50	11	0,110	0,0367
8	78,00-81,00	79,50	11	0,110	0,0367
9	81,00-84,00	82,50	8	0,080	0,0267

5. 
   Строим полигон частот и гистограмму относительных частот, масштаб на осях координат разные.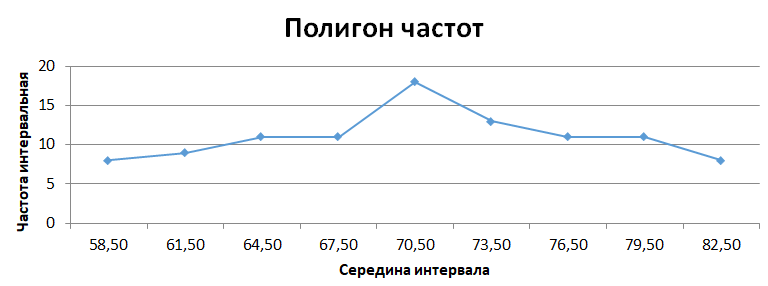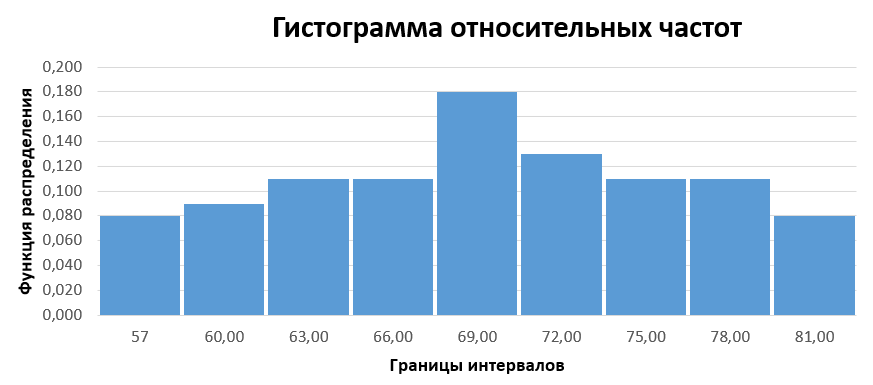
   

Эмпирическая функция распределения

1. 
   Находим значения функции распределения 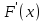в граничных точках частичных интервалов по формулам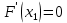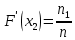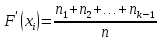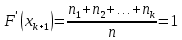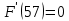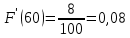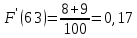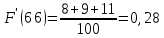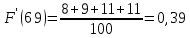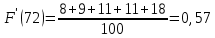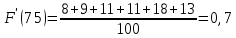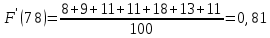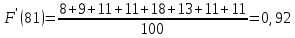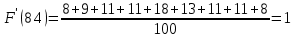
   

Строим приближенный график эмпирической функции распределения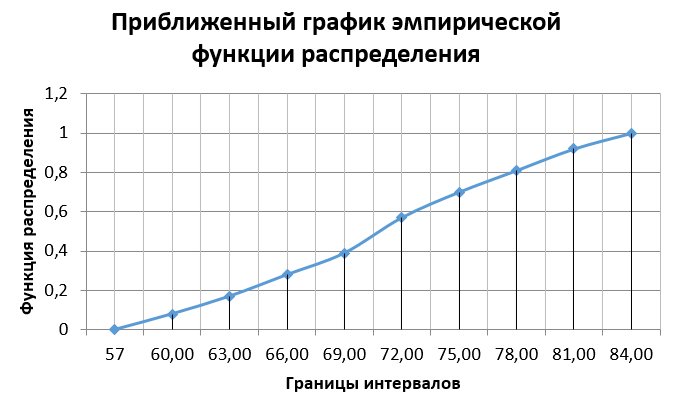

Числовые характеристики выборки

Составляем расчетную таблицу

mi	Границы интервалов		Середина интервала		Частота интервала
1	57,00-60,00		58,50		8	468		3422,25		27378
2	60,00-63,00		61,50		9	553,5		3782,25		34040,25
3	63,00-66,00		64,50		11	709,5		4160,25		45762,75
4	66,00-69,00		67,50		11	742,5		4556,25		50118,75
5	69,00-72,00		70,50		18	1269		4970,25		89464,5
6	72,00-75,00		73,50		13	955,5		5402,25		70229,25
7	75,00-78,00		76,50		11	841,5		5852,25		64374,75
8	78,00-81,00		79,50		11	874,5		6320,25		69522,75
9	81,00-84,00		82,50		8	660		6806,25		54450
Сумма				100		7074			505341

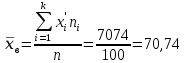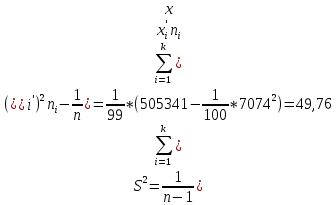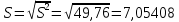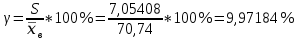В результате проведенных расчетов получены следующие результаты:

1. 
   Математическое ожидание предела прочности некоторого элемента строительной конструкции из дюралюминиевого сплава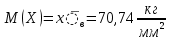
   

2. 
   Дисперсия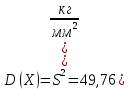
   

3. 
   Среднее квадратическое отклонение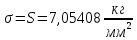
   

4. 
   Коэффициент вариации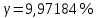
   

5. 
   Мода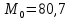
   

6. 
   Медиана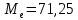
   

Вывод: среднее статистическое значение придела прочности некоторого элемента строительной конструкции из дюралюминиевого сплава равно 70,74 +7,05408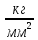