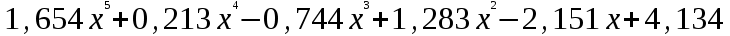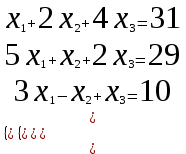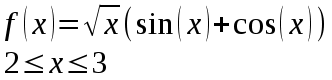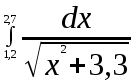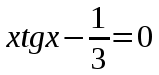Знакомство с системой Матлаб. Решение простейших задач в системе Матлаб. АвтИнжРасч. Отчет по лабораторной работе 1. Тема Знакомство с системой Матлаб. Решение простейших задач в системе Матлаб Вариант Студент Группа е 4
 Скачать 48.27 Kb. Скачать 48.27 Kb.
|
|
Балтийский государственный технический университет “Военмех” Отчет по лабораторной работе №1. Тема: Знакомство с системой Матлаб. Решение простейших задач в системе Матлаб Вариант № Студент Группа Е – 4 Преподаватель Лазарева Т.И. Санкт-Петербург 2020 Цель работы – познакомиться с интерактивным пакетом Matlab 6, предназначенным для решения широкого круга инженерных и математических задач. В первой лабораторной работе студент должен научиться задавать вектора и матрицы, выполнять различные действия с ними, использовать встроенные функции для их обработки, а также изучить средства графического отображения результатов расчета и освоить создание скрипт файлов. Постановка задачи – лабораторная работа состоит из шести заданий: вычисление функции на заданном отрезке; выполнение действий с векторами; формирование и выполнение действия с матрицами; построение графиков двух функций на заданном интервале; построение графика функции двух переменных; создание скрипт файла. Задание№1. Вычислить N значений функции на заданном отрезке. На экран вывести значения аргумента и значения функции. 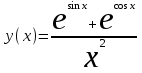 [ [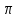 ,3 ,3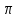 ] N=8 ] N=8Решение. >> x=linspace(pi,3*pi,8) x = 3.1416 4.0392 4.9368 5.8344 6.7320 7.6296 8.5272 9.4248 >> y=exp(sin(x))+exp(cos(x))/x.^2 y = 1.0185 0.4760 0.3957 0.6664 1.5617 2.6694 2.2039 1.0185 Задание №2. Для заданных векторов aи bдлины n (значения элементов векторов и их длину студент задает сам) выполнить преобразования и вычисления в соответствии с вариантом. Вычислить среднее арифметическое элементов 2х векторов. упорядочить вектора по возрастанию. Решение. >> >> A=[5 9 8 6]; B=[3 1 7 4]; >> A1=sort(A) A1 = 5 6 8 9 >> B1=sort(B) B1 = 1 3 4 7 >> m1=mean(A) m1 = 7 >> m2=mean(B) m2 = 3.7500 >> m3=(m1+m2)/2 m3 = 5.3750 Задание №3. При помощи встроенных функций для заполнения стандартных матриц, индексации двоеточием и, возможно, объединения, поворота или транспонирования получить следующие матрицы. Применить функции обработки данных и поэлементные операции для нахождения заданных величин. A= 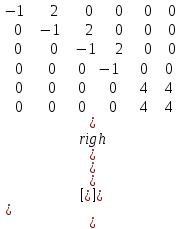 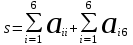 Решение. >> M=(-1)*eye(4) M = -1 0 0 0 0 -1 0 0 0 0 -1 0 0 0 0 -1 >> M(5:6,5:6)=4 M = -1 0 0 0 0 0 0 -1 0 0 0 0 0 0 -1 0 0 0 0 0 0 -1 0 0 0 0 0 0 4 4 0 0 0 0 4 4 >> M(1,2)=2; >>M(2,3)=2; >>M(3,4)=2 M = -1 2 0 0 0 0 0 -1 2 0 0 0 0 0 -1 2 0 0 0 0 0 -1 0 0 0 0 0 0 4 4 0 0 0 0 4 4 >> M1=sum(M) M1 = -1 1 1 1 8 8 >> M2=sum(M(6,:)) M2 = 8 S=M1+M2 S = 7 9 9 9 16 16 Задание №4. 4.1. Построить графики двух функций на заданных интервалах. Вывести графики: в разных окнах в одном окне в одних осях в одном окне в разных осях Использовать различные цвета, стили, подписи, легенду. Нанести сетку. 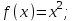 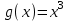 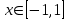 Решение. - В разных окнах: x=linspace(-1,1,10); f=x.^2; g=x.^3; figure plot(x,f,'*r-') legend('x^2') grid on hold on; figure plot(x,g,'+g--') legend('x^3') grid on - В одном окне в одних осях: x=linspace(-1,1,10); f=x.^2; g=x.^3; plot(x,f,'*r-') legend('x^2') grid on hold on; plot(x,g,'+y--') legend('x^3') grid on - В одном окне в разных осях: >> x=linspace(-1,1,10); f=x.^2; g=x.^3; subplot(2,2,1); plot(x,f,'*r-'); legend('x^2') grid on; subplot(2,2,2); plot(x,g,'+y--'); legend('x^3') grid on; 4.2.Построить график кусочно-заданной функции, отобразить ветви разными цветами и маркерами. 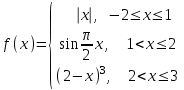 Решение. >> x1=linspace(-3,-1,20); >> x2=linspace(1.1,2,20); >> x3=linspace(2.1,3,20); >> y1=abs(x1); >> y2=sin(pi/2)*x2; >> y3=(2-x3).^3; >> plot(x1,y1,'*r',x2,y2,'+g',x3,y3,'*b-'); grid on Задание №5. Построить график функции двух переменных. Функция z Аргумент x Аргумент y 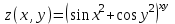 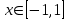 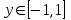 Решение. >> x=linspace(-1,1,100); y=linspace(-1,1,100); [x,y]=meshgrid(x,y); z=(sin(x.^2)+cos(y.^2)).^x.*y; plot3(x,y,z); grid on Задание №6. Написать скрипт-файл для решения следующей задачи. Заменить максимальный элемент вектора средним значением всех его элементов. Решение. >> z=[104 41 51 662 62 87 42 -44 62 8] z = 104 41 51 662 62 87 42 -44 62 8 [Y,X]=max(z) Y = 662 X = 4 Y=mean(z) Y = 107.5000 z(X)=mean(z) z = Columns 1 through 8 104.0000 41.0000 51.0000 107.5000 62.0000 87.0000 42.0000 -44.0000 Columns 9 through 10 62.0000 8.0000 индивидуальное задание №2 |