Отчет по лабораторной работе 118 Определение отношения удельных теплоемкостей воздуха
 Скачать 241.26 Kb. Скачать 241.26 Kb.
|
|
Нижегородский государственный университет им. Н. И. Лобачевского Отчет по лабораторной работе № 118 «Определение отношения удельных теплоемкостей воздуха» Дата протокола __.__.20 Дата отчета __.__.20 Выполнила: Студентка 1 курса ВШ ОПФ Петрова Ирина Проверил:к.ф.-м.н. Викторов Михаил Евгеньевич Цель работы: найти отношение удельных теплоёмкостей (коэффициент Пуассона) воздуха методом Клемана-Дезорма. Приборы и оборудование: экспериментальная установка, 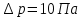 , ,  . .Теоретическая часть Обозначим  - удельную теплоёмкость газа при постоянном объёме и - удельную теплоёмкость газа при постоянном объёме и  - удельную теплоёмкость газа при постоянном давлении. При адиабатическом изменении состояния газа без теплообмена между газом и окружающей средой имеет место закон Пуассона: - удельную теплоёмкость газа при постоянном давлении. При адиабатическом изменении состояния газа без теплообмена между газом и окружающей средой имеет место закон Пуассона: , (1) , (1)где p – давление,  – удельный объём, а – удельный объём, а 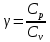 – коэффициент Пуассона. – коэффициент Пуассона.Очень быстро протекающие процессы можно считать адиабатическими. Рассмотрим опыт Клемана-Дезорма: 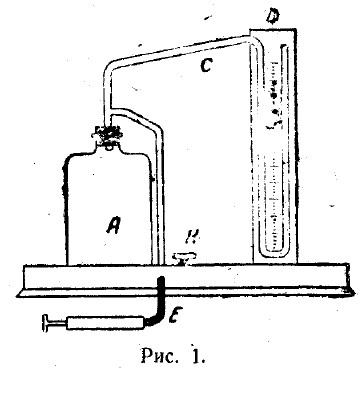 Большой толстостенный стеклянный сосуд при помощи крана может сообщаться с наружным воздухом (см. рис. 1). При помощи трубки он сообщается с водяным манометром и с нагнетательным насосом. Закроем кран и накачаем в сосуд воздух, тогда в нем воздух окажется под давлением Большой толстостенный стеклянный сосуд при помощи крана может сообщаться с наружным воздухом (см. рис. 1). При помощи трубки он сообщается с водяным манометром и с нагнетательным насосом. Закроем кран и накачаем в сосуд воздух, тогда в нем воздух окажется под давлением 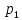 большем атмосферного. Соответственно удельный объём его по истечении некоторого времени, в течение которого температура внутри сосуда сравняется с наружной, будет большем атмосферного. Соответственно удельный объём его по истечении некоторого времени, в течение которого температура внутри сосуда сравняется с наружной, будет 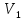 , следовательно, состояние воздуха характеризуется параметрами: , следовательно, состояние воздуха характеризуется параметрами: 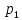 , , 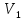 , t. Быстро откроем и быстро закроем кран, при этом воздух в сосуде быстро расширяется адиабатически и охлаждается до температуры , t. Быстро откроем и быстро закроем кран, при этом воздух в сосуде быстро расширяется адиабатически и охлаждается до температуры 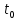 ниже комнатной, давление его поднимается до атмосферного ниже комнатной, давление его поднимается до атмосферного  , а удельный объём увеличивается до удельного объёма , а удельный объём увеличивается до удельного объёма 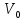 . Переход из первого состояния во второе происходит по адиабате: . Переход из первого состояния во второе происходит по адиабате: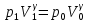 (2) (2)Рассмотрим еще третье состояние воздуха, в которое он приходит спустя некоторое время после закрытия крана. Он нагревается до температуры комнаты, равной t, и в силу этого давление его повышается до 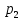 . Переход из первого состояния в третье совершается по закону . Переход из первого состояния в третье совершается по закону (3) (3)Найдем отношение удельных объемов и подставим его в (2):  и и 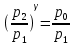 (4) (4)Решая это уравнение относительно γ получим:  (5) (5)Так как 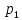 , ,  и и 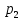 лишь мало разнятся друг от друга, то можно писать лишь мало разнятся друг от друга, то можно писать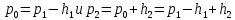 , (6) , (6)где 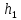 –высота манометра в 1 состоянии, –высота манометра в 1 состоянии,  – в третьем. Тогда имеем: – в третьем. Тогда имеем: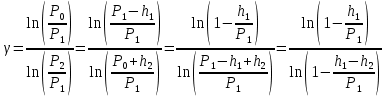 (7) (7)Т.к. 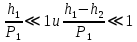 , то можно разложить формуле Тейлора и ограничиться только первым членом разложения, тогда окончательно получим: , то можно разложить формуле Тейлора и ограничиться только первым членом разложения, тогда окончательно получим: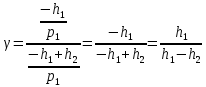 (8) (8)Экспериментальная часть При закрытом кране ждем, когда насос накачает воздух в сосуд до тех пор, пока манометр не покажет разности давлений между воздухом внутри сосуда и наружным 30-40 см. Затем закроем трубку зажимами, ждем, пока воздух в сосуде не примет значения комнатной температуры, т.е. давление внутри и, значит, разности уровней жидкости в манометре перестанут меняться. Затем откроем кран до прекращения свиста воздуха и быстро закроем его. Будем наблюдать за разностью уровней жидкости 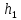 и и  . Результаты занесем в таблицу 1. . Результаты занесем в таблицу 1.
Таблица 1 Получим среднее значение коэффициента 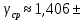 0,063, что при атмосферном давлении в 746 мм рт.ст.( 0,063, что при атмосферном давлении в 746 мм рт.ст.( и температуре воздуха, равной 25ºC, вполне удовлетворяет табличному результату в и температуре воздуха, равной 25ºC, вполне удовлетворяет табличному результату в  . . Рис.2 И 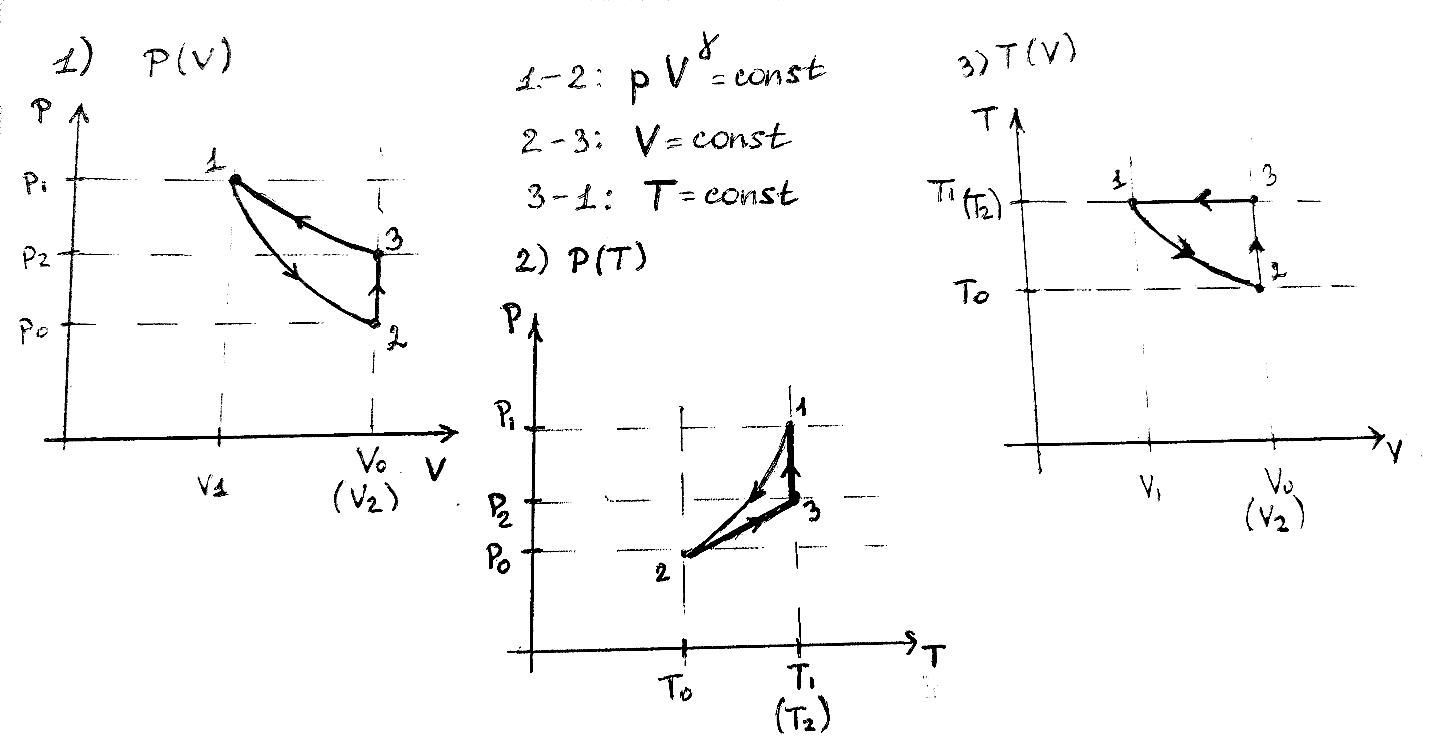 зобразим равновесные состояния, при которых производились расчеты, и процессы перехода между ними. (см.рис.2) зобразим равновесные состояния, при которых производились расчеты, и процессы перехода между ними. (см.рис.2)Процесс 1-2 является адиабатическим, 2-3 изохорическим, а 3-1 изотермическим, запишем уравнения кривых цикла для каждого из них (здесь A,B,C,D – некоторые константы). 1-2. Будем использовать адиабату Пуассона и уравнение Клайперона-Менделеева: 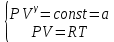 ; ;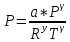 ; ;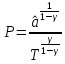 =A =A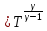 Аналогично выведем зависимость T(V): 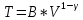 . .2-3. Из уравнения Клайперона-Менделеева имеем: 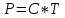 3-1.С помощью таких же рассуждений приходим к следующему уравнению  . .Теплоемкостью мы называем количество тепла, которое нужно сообщить системе, чтобы изменить ее температуру на 1К,  - удельную теплоёмкость газа при постоянном объёме и - удельную теплоёмкость газа при постоянном объёме и  - удельную теплоёмкость газа при постоянном давлении. Покажем, что для идеального газа - удельную теплоёмкость газа при постоянном давлении. Покажем, что для идеального газа  . .По определению 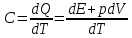 , ,  , ,  = =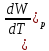 . Принцип Ле-Шателье гласит: внешнее воздействие, выводящее систему из термодинамического равновесия, вызывает в ней компенсирующие процессы. Рассмотрим следующую ситуацию: дан сосуд с поршнем (зафиксируем его), воздух в нем занимает объем V=const, если мы сообщим ему некоторое количество теплоты . Принцип Ле-Шателье гласит: внешнее воздействие, выводящее систему из термодинамического равновесия, вызывает в ней компенсирующие процессы. Рассмотрим следующую ситуацию: дан сосуд с поршнем (зафиксируем его), воздух в нем занимает объем V=const, если мы сообщим ему некоторое количество теплоты 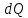 , то в результате такого воздействия давление и температура изменятся соответствующим образом , то в результате такого воздействия давление и температура изменятся соответствующим образом  . Если мы позволим поршню двигаться, то система сможет изменить и объем Vдля компенсации, а значит, давление и температура будут меняться уже меньше ( . Если мы позволим поршню двигаться, то система сможет изменить и объем Vдля компенсации, а значит, давление и температура будут меняться уже меньше (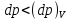 , , 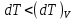 ). Можем подобрать процесс так, что он будет проходить изобарно ( ). Можем подобрать процесс так, что он будет проходить изобарно ( соответствующее изменение температуры соответствующее изменение температуры 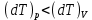 , а значит и , а значит и  . .Распишем  детально: детально: 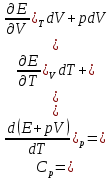 , но , но  , т.к. энергия при заданной температуре не меняется (для идеального газа взаимодействие между частицами отсутствует, а изменение энергии от объема не зависит). Тогда имеем: , т.к. энергия при заданной температуре не меняется (для идеального газа взаимодействие между частицами отсутствует, а изменение энергии от объема не зависит). Тогда имеем: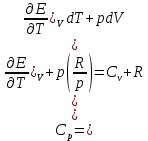 –известное соотношение Роберта Майера. Т.к. R –известное соотношение Роберта Майера. Т.к. R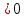 , то и , то и  . .Оценим величину понижения температуры, происходившей в опыте. Вновь запишем уравнение адиабаты Пуассона для эксперимента в таком виде: 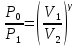 . Перейдем к зависимости от температуры, учитывая, что . Перейдем к зависимости от температуры, учитывая, что 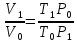 : :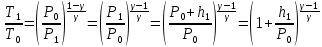 (9) (9)Величина 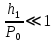 , значит, можно разложить формуле Тейлора и ограничиться только первым членом разложения, тогда окончательно получим: , значит, можно разложить формуле Тейлора и ограничиться только первым членом разложения, тогда окончательно получим: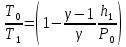 Тогда температура изменится на величину 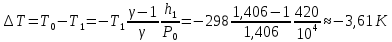 . .Вычислим количество воздуха, выходящего из сосуда, когда открывается кран. Переход из первого состояния во второе происходит по адиабате: 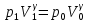 Но 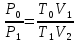 ,а ,а 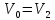 тогда имеем: тогда имеем: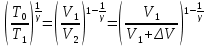 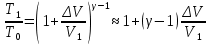 Использовали разложение Тейлора, т.к. 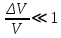 , выразим изменение объема с помощью формулы (9): , выразим изменение объема с помощью формулы (9):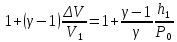 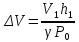 (10) (10)Вспомним, что процесс 3-1 изотермический, учитывая (6), имеем: 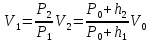 (11) (11)Когда воздух вытекает из сосуда, его количество вещества меняется на величину 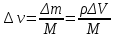 , подставим сюда (10) и (11): , подставим сюда (10) и (11):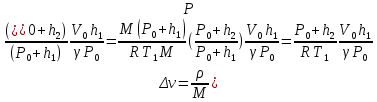 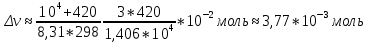 Вывод: Найденное отношение удельных теплоёмкостей воздуха методом Клемана-Дезорма вполне соответствует табличному значению (погрешность определения составила порядка 4%) Температура в сосуде в ходе эксперимента понижается почти на 4К, а за то время, пока кран открыт, из сосуда вытекает около 4 ммоль воздуха |