Отчёт по лабораторной работе 13
 Скачать 77.89 Kb. Скачать 77.89 Kb.
|
|
ПЕРВОЕ ВЫСШЕЕ ТЕХНИЧЕСКОЕ УЧЕБНОЕ ЗАВЕДЕНИЕ РОССИИ  МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ федеральное государственное бюджетное образовательное учреждение высшего образования «САНКТ-ПЕТЕРБУРГСКИЙ ГОРНЫЙ УНИВЕРСИТЕТ» Кафедра общей и технической физики Отчёт по лабораторной работе №13
Санкт-Петербург 2019 год. 1. Цель работы: определить коэффициент вязкости жидкости методом Стокса. 2. Краткое теоретическое обоснование. 1. В данной работе изучается вязкость жидкости. При перемешивании жидкости между ее слоями возникают силы внутреннего трения, действующие таким образом, что скорости всех слоев жидкости выравниваются. При этом со стороны слоя, движущегося медленно, на более быстрый слой действует задерживающая сила. Но со стороны слоя, двигающегося быстро, действует ускоряющая сила. Это обуславливается явлением вязкости. 2. Вязкость (внутр. трение) – свойство реальных жидкостей и газов оказывать сопротивление перемещению одной части жидкости(газа) относительно другой. Коэффициент вязкости – коэффициент, характеризующий данную жидкость. Сила трения – сила, возникающая между соприкасающимися телами. Сила тяжести – сила, с которой тело действует на опору или растягивает подвес. Выталкивающая сила (сила Архимеда) – сила, действующая на тело, погруженное в жидкость. Ламинарное течение – течение, при котором вдоль потока каждый выделенный тонкий слой скользит относительно соседних, не перемешиваясь с ними. Турбулентное течение – течение, при котором вдоль потока происходит интенсивное вихреобразование и перемешивание жидкости (газа). Градиент скорости – это отношение  , которое показывает, как быстро меняется скорость при переходе от слоя к слою в направлении x, перпендикулярном направлению движения слоев. , которое показывает, как быстро меняется скорость при переходе от слоя к слою в направлении x, перпендикулярном направлению движения слоев.3. Сила трения между плоскими слоями при их движении согласно з-ну Ньютона равна: 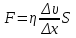 где - коэффициент пропорциональности, называемый коэффициентом вязкости или динамической вязкостью; S - площадь соприкосновения слоев,  - разница в скорости между соседними слоями, - разница в скорости между соседними слоями, 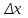 - расстояние между соседними слоями. - расстояние между соседними слоями.Соотношение силы трения шарика с его скоростью и радиусом при малых значениях скорости выражается следующей формулой: 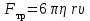 , ,где  - коэффициент вязкости, r- радиус шарика, - коэффициент вязкости, r- радиус шарика, 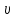 - скорость движения шарика; - скорость движения шарика;По второму закону Ньютона:  , ,где Р- сила тяжести, действующая на шарик, FА- сила Архимеда, Fтр- сила внутреннего трения; Сила тяжести вычисляется по формуле:  , ,где м - плотность материала шарика; V – объем шарика; Выталкивающая сила по закону Архимеда: 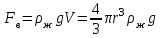 . .4. В данной лабораторной работе ожидается получить коэффициент вязкости касторового масла, равный 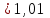 . .3. Схема установки.  - сила внутреннего трения, Н, - сила внутреннего трения, Н, - выталкивающая сила, Н, - выталкивающая сила, Н,P – сила тяжести, Н.  4. Основные расчетные формулы. 1. Коэффициент вязкости:  , , где  - коэффициент вязкости, Па·с, - коэффициент вязкости, Па·с,r - радиус шарика, м, 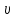 - скорость движения шарика, м/с, - скорость движения шарика, м/с, - плотность жидкости, кг/ - плотность жидкости, кг/  - плотность материала шарика, кг/ - плотность материала шарика, кг/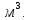 2. Среднее значение коэффициента вязкости:  3. Скорость при равномерном движении 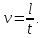 5. Формула расчета средней квадратичной погрешности.  где 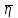 - среднее значение коэффициента вязкости, - среднее значение коэффициента вязкости, 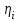 - значение коэффициента вязкости в каждом отдельном опыте, n- количество опытов. - значение коэффициента вязкости в каждом отдельном опыте, n- количество опытов.6. Таблица измерений и вычислений.
Погрешности прямых измерений: 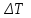 =0,1К; =0,1К;  =5·10-5м; =5·10-5м;  = 5·10-5м; = 5·10-5м;  =0,01с. =0,01с.7. Расчет результатов эксперимента. Расчет коэффициента вязкости жидкости для одного опыта: 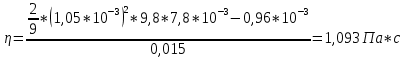 Расчет среднего значения коэффициента вязкости жидкости: 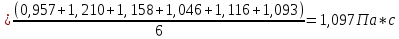 3. Средняя квадратичная погрешность: 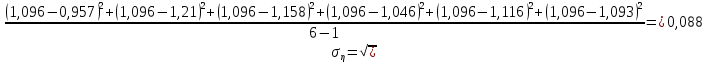 Окончательный результат:  = 1,097 = 1,097 0,088 Па*с 0,088 Па*с8. Вывод: В данной работе экспериментально был определен коэффициент вязкости жидкости. Путем постановки нескольких опытов со стальными и свинцовыми шариками, удалось установить, что скорость шарика, движущегося в сосуде с жидкостью, зависит от размеров и плотности шарика. Полученный результат имеет малую погрешность, а значит в работе присутствуют довольно незначительные погрешности в измерениях и вычислениях. |

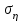
 *103
*103