Отчет по лабораторной работе 2 Анализ факторов, влияющих на устойчивость моделирования на примере анализа адаптивной системы управления
 Скачать 0.77 Mb. Скачать 0.77 Mb.
|
|
Министерство науки и высшего образования Российской Федерации ФГБОУ ВО Кубанский государственный технологический университет Армавирский механико-технологический институт Кафедра внутризаводского электрооборудования и автоматики Отчет по лабораторной работе №2 «Анализ факторов, влияющих на устойчивость моделирования на примере анализа адаптивной системы управления» по дисциплине: «Теория решения изобретательских задач» направление 13.03.02 Электроэнергетика и электротехника Выполнил студент: Чередняков И.А. Группа 17-ФАБ-ЭЭ Проверил ст. преподаватель: Орлов Сергей Павлович Армавир 2021 Цель работы: проанализировать факторы, влияющие на устойчивость моделирования на примере анализа адаптивной системы управления. Порядок выполнения работы: 1. Научиться анализировать результаты компьютерного моделирования. 2. Приобрести навыки построения моделей на примере подсистемы моделирования Simulink системы Matlab. 3. Научиться определять влияние структуры алгоритма расчета и иных факторов, влияющих на устойчивость моделирования на примере сравнения неадаптивной и адаптивной систем управления. 4. Выполнить задание согласно своему варианту. 5. Оформить отчет о выполнении работы. Ход работы: Вариант №15. Задание 1. Построить структуру Simulink - модели неадаптивную систему на базе регулятора (6), значений параметров (1) и значений эталонной модели (3), а так же синтезировать Simulink - модель, включающую алгоритм адаптации (8) и подключить его к настраиваемому регулятору (7). Отладку Simulink - модели произвести экспериментально при помощи коэффициента адаптации  . Провести моделирование системы в условиях скачкообразного трехкратного увеличения параметра . Провести моделирование системы в условиях скачкообразного трехкратного увеличения параметра 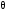 и построить два графика. На одном графике построить x и и построить два графика. На одном графике построить x и 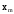 в зависимости от времени, на другом – u в зависимости от времени. в зависимости от времени, на другом – u в зависимости от времени.Таблица 1 – Таблица исходных данных
Имеется технический объект (система), описываемый уравнением вида:  (1) (1)где х – переменная состояния (вектор состояния) объекта; u - сигнал управления (входной вектор управляемых переменных); 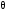 - неизвестный постоянный параметр. - неизвестный постоянный параметр.Эталонная модель описывается передаточной функцией:  (3) (3)где g – сигнал задания;  > 0 – параметр, задающий время переходного процесса. > 0 – параметр, задающий время переходного процесса.Эталонная модель (3) определяет желаемое качество слежения объекта (1) за сигналом задания g. Вычислим производную ошибки слежения ε по времени с учетом (1) и (3):  (4) (4)Одна из теорем адаптивных систем доказывает, что ошибка слежения экспоненциально будет стремиться к нулю, если выполняется равенство: 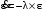 (5) (5)Уравняем правых частей уравнения (4) и уравнения (5) получим: 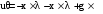 (6) (6)Итак, если известно значение параметра 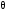 закон управления (6) обеспечивает для объекта (1) выполнение целевого равенства (2). закон управления (6) обеспечивает для объекта (1) выполнение целевого равенства (2).Усложняем задачу, что имеет место в действительности, пусть параметр 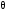 неизвестен. неизвестен.Тогда закон управления (6) также должен соблюдаться, но параметр 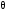 следует заменить на такой же вычисленный (оцениваемый) параметр обозначаемый следует заменить на такой же вычисленный (оцениваемый) параметр обозначаемый 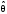 : : (7) (7)Таким образом, необходимо ввести регулятор для нахождения функции 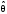 , которая обеспечит устойчивость замкнутой системы и цель управления (2). , которая обеспечит устойчивость замкнутой системы и цель управления (2).Теоретическое обоснование и выбор функции Ляпунова достаточно сложен, приводить его будем. Подчеркнем, что выбор функции Ляпунова позволяет сразу определить устойчивость без решения системы дифференциальных уравнений. При выборе оцениваемого параметра в виде: 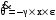 (8) (8)Производная функция Ляпунова отрицательная, тем самым обеспечивается устойчивость системы в целом. Алгоритм управления наделяет замкнутую систему следующими свойствами: 1. Устойчивость замкнутой системы и ограниченность всех сигналов; 2. Асимптотическое стремление ошибки  к нулю; к нулю;3. Асимптотическое стремление 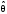 к к 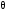 (при ненулевом х); (при ненулевом х);4. Увеличение скорости сходимости параметрической ошибки к нулю при увеличении коэффициента  до некоторого оптимального значения. Дальнейшее повышение до некоторого оптимального значения. Дальнейшее повышение  приведет к снижению скорости сходимости ошибки и появлению колебаний в системы. приведет к снижению скорости сходимости ошибки и появлению колебаний в системы.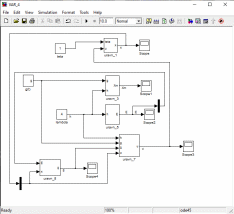 Рисунок 1 – Структура Simulink - модели, решающей систему уравнений. 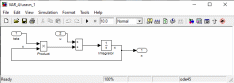 Рисунок 2 – Блок Simulink соответствующей модели уравнения (1)  Рисунок 3 – Блок Simulink соответствующей модели уравнения (3)  Рисунок 4 – Блок Simulink соответствующей модели уравнения (5) 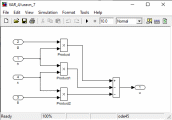 Рисунок 5 – Блок Simulink соответствующей модели уравнения (7)  Рисунок 6 – Блок Simulink соответствующей модели уравнения (8) 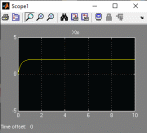 Рисунок 7 – 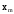 в зависимости от времени в зависимости от времени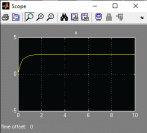 Рисунок 8 – x в зависимости от времени 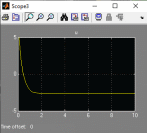 Рисунок 9 – u в зависимости от времени Вывод: в результате лабораторной работы мы научились анализировать факторы, влияющие на устойчивость моделирования на примере анализа адаптивной системы управления. |
