Численное решение нелинейных уравнений и систем линейных уравнений. ЛР2. Отчет по лабораторной работе 2 Численное решение нелинейных уравнений и систем линейных уравнений по курсу Вычислительные задачи систем автоматизации
 Скачать 1.6 Mb. Скачать 1.6 Mb.
|
|
Министерство науки и высшего образования Российской Федерации СЕВЕРСКИЙ ТЕХНОЛОГИЧЕСКИЙ ИНСТИТУТ – филиал федерального государственного автономного образовательного учреждения высшего образования «Национальный исследовательский ядерный университет «МИФИ»  (СТИ НИЯУ МИФИ) (СТИ НИЯУ МИФИ)Кафедра ВМ и ИТ Отчет по лабораторной работе №2 «Численное решение нелинейных уравнений и систем линейных уравнений по курсу «Вычислительные задачи систем автоматизации» Выполнил студент гр. Д-278 Баннов В.Е. Северск 2020 Аппроксимация – научный метод, состоящий в замене одних объектов другими, в каком-то смысле близкими к исходным, но более простыми. Аппроксимация позволяет исследовать числовые характеристики и качественные свойства объекта, сводя задачу к изучению более простых или более удобных объектов. Интерполяция – в вычислительной математике способ нахождения промежуточных значений величины по имеющемуся дискретному набору известных значений. Экстраполяция – особый тип аппроксимации, при котором функция аппроксимируется вне заданного интервала, а не между заданными значениями. Задача интерполирования состоит в том, чтобы по значениям функции f(x) в нескольких точках отрезка восстановить её значения в остальных точках этого отрезка. Интерполяционный полином Лагранжа: 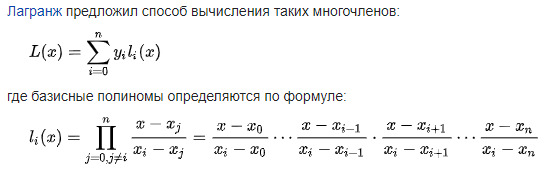 Интерполяционный полином Ньютона: 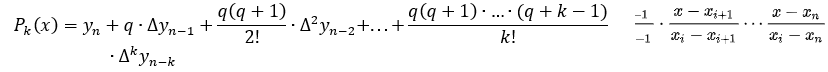 Практическая часть Блок-схема для построения интерполяционного многочлена Лагранжа 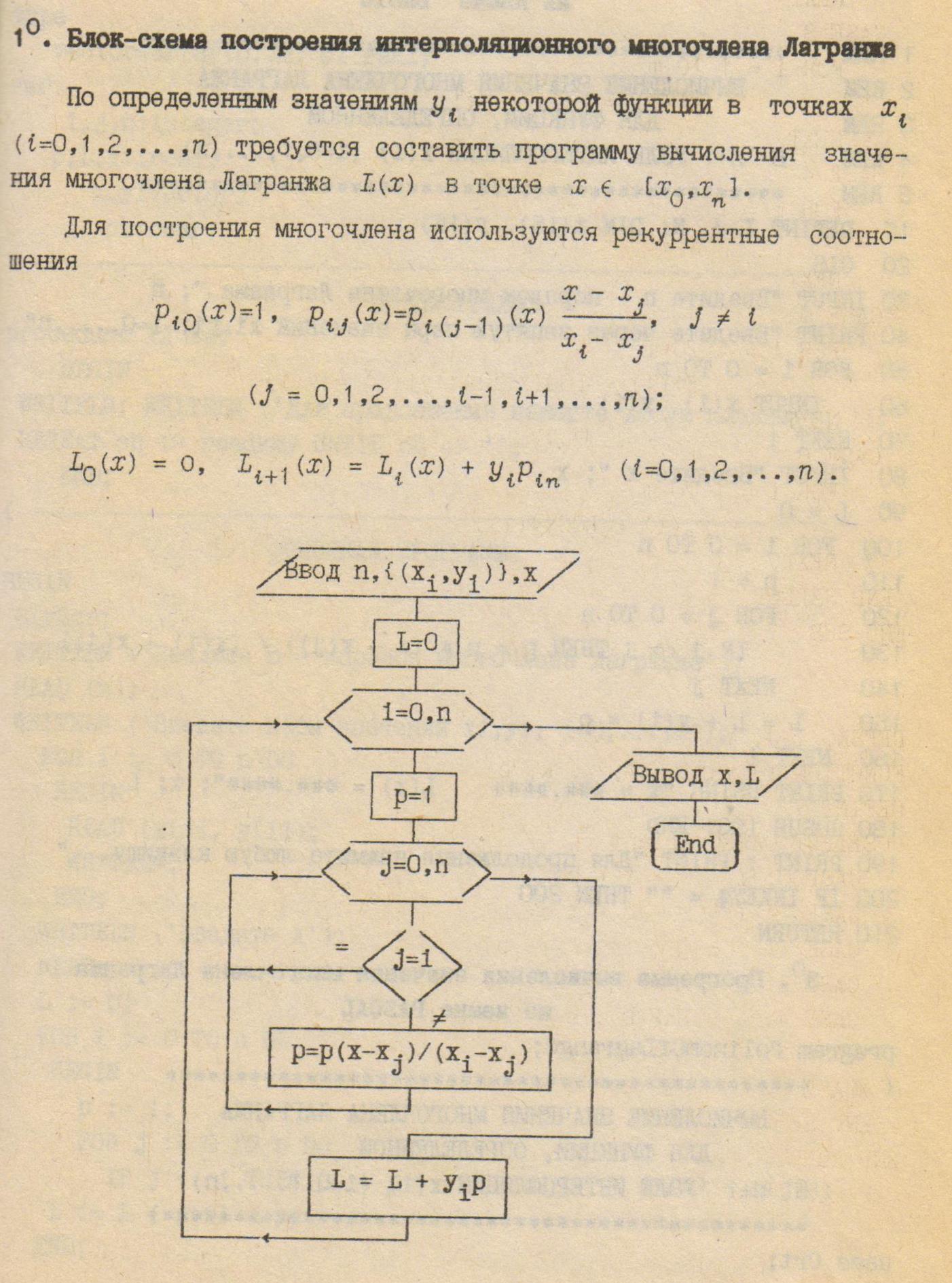 Был решен тестовый пример ИПЛ
Для поиска решения была составлена программа, реализующая решение данного ИПЛ Код программы: 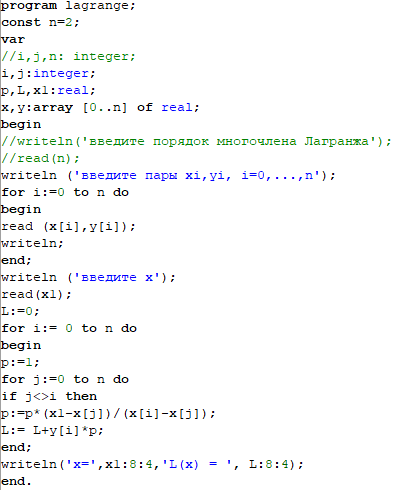 Результат:  2) Был решен пример из варианта № 3
Для поиска решения была составлена программа, реализующая решение данного ИПЛ Код программы:  Результат:  Результат вычислений вручную:  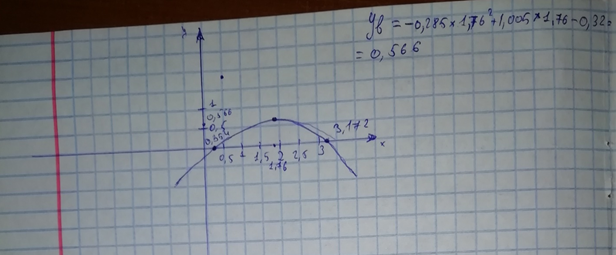 2. Метод наименьших квадратов Был решен пример:
Для решения была создана программа Exel, реализующая метод наименьших квадратов 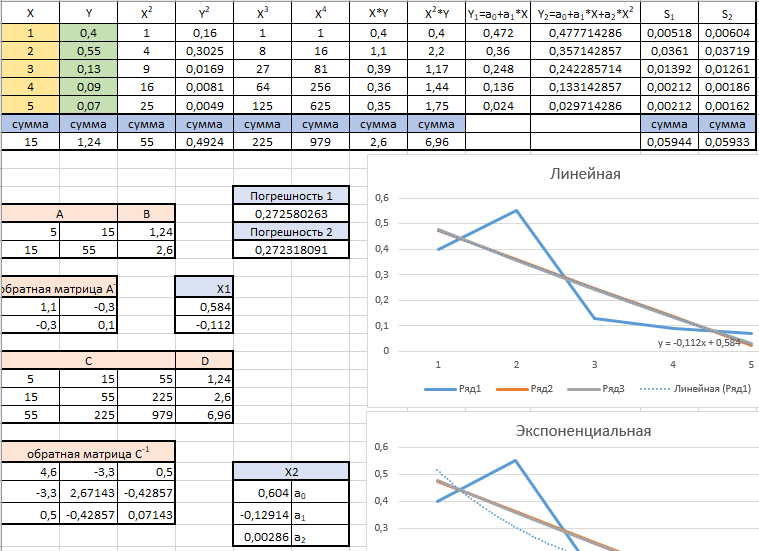 Построены графики 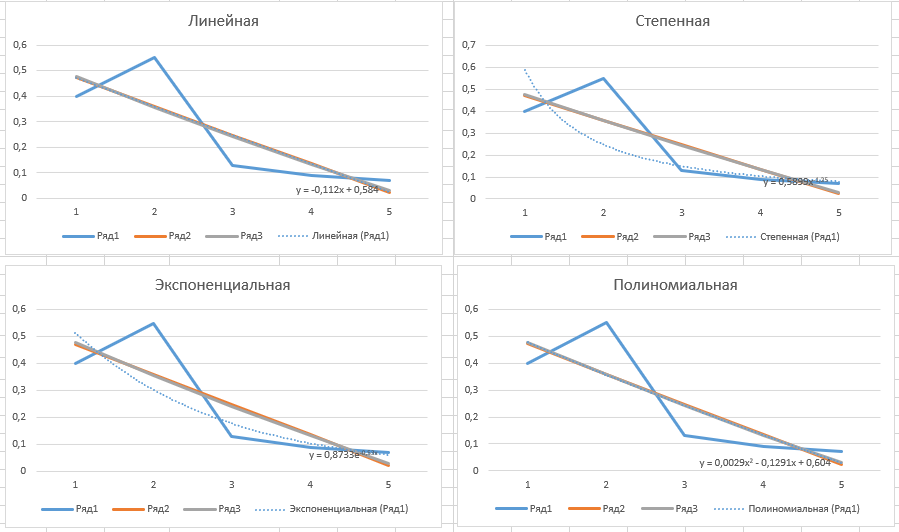 Результаты расчетов вручную:  Вывод В ходе проделанной работы я изучил метод интерполирования полиномом Лагранжа, также метод наименьших квадратов для приближения функций, заданных таблицей. Для ИПЛ с помощью программы получили: у=0,566 Результат расчетов вручную: y=0,566 Для метода наименьших квадратов расчитали у1 и у2, сравнили с урасчетное:
|
