Краевая (ГЛОССАРИЙ). Глоссарий глоссарий аппроксимация
 Скачать 2.16 Mb. Скачать 2.16 Mb.
|
|
ГЛОССАРИЙ ГЛОССАРИЙ Аппроксимация (от лат. proxima — ближайшая) или приближе́ние — научный метод, состоящий в замене одних объектов другими, в каком-то смысле близкими к исходным, но более простыми.Аппроксимация позволяет исследовать числовые характеристики и качественные свойства объекта, сводя задачу к изучению более простых или более удобных объектов (например, таких, характеристики которых легко вычисляются или свойства которых уже известны). Аппроксима́ция (от лат. proxima — ближайшая) или приближение — научный метод, состоящий в замене одних объектов другими, в каком-то смысле близкими к исходным, но более простыми. Вычислительные (численные) методы — методы решения математических задач в численном виде. Представление как исходных данных в задаче, так и её решения — в виде числа или набора чисел. Многие численные методы являются частью библиотек математических программ Гиперболические уравнения — класс дифференциальных уравнений в частных производных. Характеризуются тем, что задача Коши с начальными данными, заданными на нехарактеристической поверхности, однозначно разрешима. Дифференциа́льное уравне́ние — уравнение, в которое входят производные функции, и может входить сама функция, независимая переменная и параметры. Порядок входящих в уравнение производных может быть различен (формально он ничем не ограничен). Производные, функции, независимые переменные и параметры могут входить в уравнение в различных комбинациях или могут отсутствовать вовсе, кроме хотя бы одной производной. Не любое уравнение, содержащее производные неизвестной функции, является дифференциальным уравнением Дифференциальное уравнение — уравнение, в которое входят производные функции, и может входить сама функция, независимая переменная и параметры Задача Дирихле — вид задач, появляющийся при решении дифференциальных уравнений в частных производных второго порядка. Названа в честь Иоганна Дирихле. Задача Коши́ — одна из основных задач теории дифференциальных уравнений (обыкновенных и с частными производными); состоит в нахождении решения (интеграла) дифференциального уравнения, удовлетворяющего так называемым начальным условиям (начальным данным). Интерполяция, интерполирование (от лат. inter–polis — «разглаженный, подновлённый, обновлённый; преобразованный») — в вычислительной математике способ нахождения промежуточных значений величины по имеющемуся дискретному набору известных значений[1]. Термин «интерполяция» впервые употребил Джон Валлис в своём трактате «Арифметика бесконечных» (1656). Корень уравнения – это такое значение буквы (переменной), при подстановке которого уравнение обращается в верное числовое равенство Краевая задача (граничная задача) — задача о нахождении решения заданного дифференциального уравнения (системы дифференциальных уравнений), удовлетворяющего краевым (граничным) условиям в концах интервала или на границе области. Линейное уравнение — это алгебраическое уравнение, у которого полная степень составляющих его многочленов равна 1. Метод конечных разностей — численный метод решения дифференциальных уравнений, основанный на замене производных разностными схемами. Является сеточным методом. Метод конечных элементов (МКЭ) — это численный метод решения дифференциальных уравнений с частными производными, а такжеинтегральных уравнений, возникающих при решении задач прикладной физики. Метод широко используется для решения задач механикидеформируемого твёрдого тела, теплообмена, гидродинамики и электродинамики. Обыкновенное дифференциальное уравнение (ОДУ) — дифференциальное уравнение для функции от одной переменной. (Этим оно отличается от уравнения в частных производных, где неизвестная — функция нескольких переменных.) Остаточный член — разность между заданной функцией и функцией её аппроксимирующей. Тем самым оценка остаточного члена является оценкой точности рассматриваемой аппроксимации. Этот термин применяется, например, в формуле ряда Тейлора Параболические уравнения — класс дифференциальных уравнений в частных производных. Один из видов уравнений, описывающихнестационарные процессы. Разностная схема — это конечная система алгебраических уравнений, поставленная в соответствие какой-либо дифференциальной задаче, содержащей дифференциальное уравнение и дополнительные условия (например краевые условия и/или начальное распределение) Расчётная (вычислительная) сетка — совокупность точек (сеточных узлов), заданных в области определения некоторой функции Решение уравнения — это задача по нахождению таких значений аргументов (чисел, функций, наборов и т. д.), при которых выполняется равенство (выражения слева и справа от знака равенства становятся эквивалентными). Система линейных алгебраических уравнений (линейная система, также употребляются аббревиатуры СЛАУ, СЛУ) — система уравнений, каждое уравнение в которой является линейным — алгебраическим уравнением первой степени. Собственный ве́ктор — понятие в линейной алгебре, определяемое для произвольного линейного оператора как ненулевой вектор, применение к которому оператора даёт коллинеарный вектор — тот же вектор, умноженный на некоторое скалярное значение. Уравнение – это равенство, содержащее неизвестное число, которое надо найти. Шаблон — это множество точек с помощью которых аппроксимируются производные. Эллиптические уравнения — класс дифференциальных уравнений в частных производных, описывающих стационарные процессы. Тесты по предмету «Численные методы решения краевых задач»          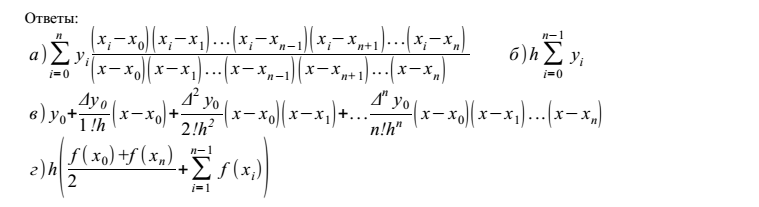 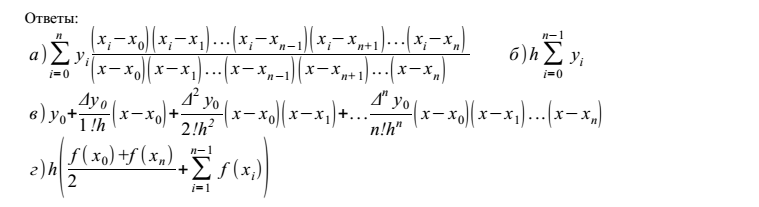 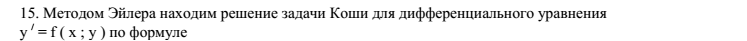       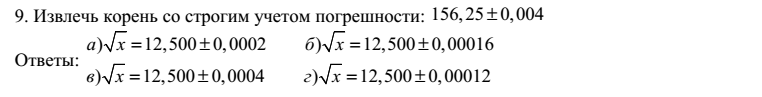          |
