Главная страница
Навигация по странице:

  • Негосударственное частное образовательное учреждение

  • Дисциплина: Физика ОТЧЕТ по ЛАБОРАТОРНОЙ РАБОТЕ № 2 « Движение с постоянным ускорением » Выполнили

  • Студентка группы А - 22101 Митин Артемий Александрович Студент группы А-22101 _______________________ Проверила

    		•

    Движение с постоянным ускорением. Отчет по лабораторной работе 2 Движение с постоянным ускорением


    Скачать 36.71 Kb.
    НазваниеОтчет по лабораторной работе 2 Движение с постоянным ускорением
    АнкорДвижение с постоянным ускорением
    Дата28.03.2023
    Размер36.71 Kb.
    Формат файлаdocx
    Имя файла1-5.docx
    ТипОтчет
    #1022369
    Негосударственное частное образовательное учреждение

    высшего образования

    «Технический университет УГМК»


    Кафедра гуманитарных и естественно - научных дисциплин
    Дисциплина: Физика
    ОТЧЕТ по ЛАБОРАТОРНОЙ РАБОТЕ № 2

    «Движение с постоянным ускорением»
    Выполнили:
    Агафонова Софья Александровна

    Студентка группы А-22101

    Митин Артемий Александрович

    Студент группы А-22101

    _______________________

    Проверила:

    Коржавина Наталья Валерьевна,

    к. п. н, доцент

    _______________________


    г. Верхняя Пышма

    2023

    Цель работы:

    1. Познакомиться с движением объекта, моделью которого является материальная точка (МТ)

    2. Исследовать движение объекта с постоянным ускорением

    3. Эксперементально определить ускорение свободного падения на поверхность Земли

    Для лабораторной работы мы использовали модель движения тела, брошенного под углом к горизонту.

    *скрин модели*

    Ход работы:

    Запишем начальные данные. h=30м - начальная высота, α=60° - начальный угол.

    Выведем формулу для максимальной высоты подъёма тела.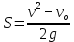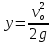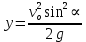

    ; ;

    1. Модель движения тела, брошенного под углом к горизонту :

    *скрин модели*

    1. При помощи (I) вычислим и запишем в табл. 1 средние значения вертикальной координаты точки максимального подъёма умах и отклонения Δумах измеренного значения от среднего:

    Таблица 1. Результаты измерений

    Номер измерения
    Траектория 1
    Траектория 2
    Траектория 3
    Траектория 4
    Траектория 5




    умах, м
    Δумах, м
    умах, м
    Δумах, м
    умах, м
    Δумах, м
    умах, м
    Δумах, м
    умах, м
    Δумах, м

    1
    38,6
    0
    41
    0
    43,8
    0
    48,5
    0
    53,9
    0

    2
    38,6
    0
    41
    0
    43,8
    0
    48,5
    0
    53,9
    0

    3
    38,6
    0
    41
    0
    43,8
    0
    48,5
    0
    53,9
    0

    4
    38,6
    0
    41
    0
    43,8
    0
    48,5
    0
    53,9
    0

    5
    38,6
    0
    41
    0
    43,8
    0
    48,5
    0
    53,9
    0

    умах, м
    38,6



    41



    43,8



    48,5



    53,9



    Абс.ош
    0
    0
    0
    0
    0



    1. При помощи таблицы с результатами измерений вычислим и запишем в таблицу 2 все необходимые характеристики.

    Таблица 2. Результаты расчётов

    Номер измерения
    1
    2
    3
    4
    5

    vo,м/c
    15
    17
    19
    22
    25

    vo2,(м/c)2
    225
    289
    361
    484
    625

    умах, м
    31,6
    41
    43,8
    48,5
    53,9

    sinα


    sin2α


    g,(м/с)2
    9,803(м/с)2



    1. Помтроим график зависимости средних значений вертикальной координатой точки максимального подъёма. Умах от квадрата начальной скорости.

    *график*

    1. При помощи графика, определим значение ускорения свободного падения g, используя формлу: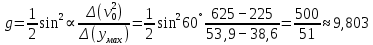
      (м/с)2

    Запишем результаты в таблицу 2 (Результаты расчётов)

    1. Вычислим ошибку среднего значение g. Т.к. мы использовали электронную модель, Δgср = 0

    Вывод: В ходе лабораторной работы ознакомились с движением объекта, моделью которого является материальная точка.

    Исследовали движение объекта с постоянным ускорением.

    Экспериментально определили ускорение свободного падения на поверхность Земли. g=(9,803±0)(м/с)2 c доверительной вероятностью 0,95, что в пределах погрешности соответствует табличному значению. Вычислили и записали в табл. 1 средние значения вертикальной координаты точки максимального подъёма умах и отклонения Δумах измеренного значения от среднего (табл.1)

    написать администратору сайта