2 лаба этм. Отчет по лабораторной работе 2 исследование электрических свойств полупроводниковых материалов
 Скачать 52.5 Kb. Скачать 52.5 Kb.
|
|
МИНОБРНАУКИ РОССИИ Санкт-Петербургский государственный электротехнический университет «ЛЭТИ» им. В.И. Ульянова (Ленина) Кафедра МНЭ отчет по лабораторной работе №2 «ИССЛЕДОВАНИЕ ЭЛЕКТРИЧЕСКИХ СВОЙСТВ ПОЛУПРОВОДНИКОВЫХ МАТЕРИАЛОВ» по дисциплине «Электротехническое материаловедение»
Санкт-Петербург 2018 Цели работы: сравнение температурных зависимостей сопротивления полупроводников с различной шириной запрещенной зоны; определение ши- рины запрещенной зоны и энергии ионизации легирующих примесей в мате- риалах. Основные понятия и определения Полупроводники – материалы с электронной электропроводностью, ко- торые по своему удельному сопротивлению занимают промежуточное поло- жение между проводниками и диэлектриками. Условный диапазон удельных сопротивлений полупроводников ограничивают значениями 10–5...108 Ом∙м. Характерной особенностью полупроводниковых материалов является сильно выраженная зависимость удельной проводимости от внешних энерге- тических воздействий, а также от концентрации и типа примесей. В зависимости от степени чистоты полупроводники подразделяются на собственные и примесные. Собственный – это такой полупроводник, в котором можно пренебречь влиянием примесей при данной температуре. Содержание примесей в них не превышает 10-9…10-8 %, и существенного влияния на удельную проводи- мость полупроводника они не оказывают. Примесный – это такой полупроводник, электрофизические свойства которого в основном определяются примесями. В общем случае удельная проводимость = en, где n и - концентрация и подвижность носителей заряда, меняющиеся с температурой. График зависимости ln(n) от 1/T условно делится на три участка. При низких температурах (1-й участок) донорные уровни заполнены электронами. С увеличением температуры (условно 2-й участок) электроны переходят в зону проводимости. Увеличивающаяся при этом концентрация электронов в зоне проводимости определяется выражением: 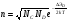 где: NC - эффективная плотность состояний в зоне проводимости, энергия которых приведена к дну зоны проводимости; ND - концентрация доноров; ЭD - энергия ионизации доноров. 3-й участок называют областью собственной проводимости. Концентрация носителей определяется выражением: 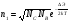 Обработка результатов эксперимента Таблица 1.1 «Экспериментальные данные»
Таблица 1.2 «Экспериментальные данные»
1. Рассчитаем удельное сопротивление исследуемых полупроводниковых материалов по экспериментальным данным для каждой температурной точки по формуле ρ = RS/l В качестве примера рассчитаем для Si при t =25: 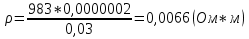 Рассчитаем для каждого материала и занесем в таблицу 2.1. Вычислим соответствующие удельные проводимости образцов по формуле γэксп = 1/ρ. Для Si при t=25: 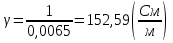 Рассчитаем для каждого материала и занесем в таблицу. Таблица 2.1 «Результаты эксперимента»
2. По данным таблицы 2.1 построим температурные зависимости удельной проводимости полупроводников, откладывая по оси абсцисс параметр 1/T, а по оси ординат – экспериментальные значения ln γэксп. Рисунок 1 «температурные зависимости удельной проводимости полупроводников» 3. Рассчитаем концентрации собственных носителей заряда в полупроводниках Si, Ge, InSb и SiC при T = 300 К по формуле: 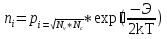 K = 8.56*10-5 эВ/К Для Si: 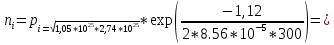 5,739E+15 м-3 5,739E+15 м-3Для Ge: 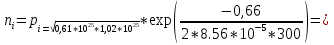 2,071E+19 м-3 2,071E+19 м-3Для SiC: 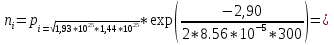 5,01 м-3 5,01 м-3Для InSb: 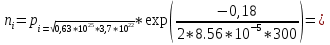 1,451E+22 м-3 1,451E+22 м-34. Оценим значения собственной удельной проводимости в этих полу- проводниках при T= 300 К: 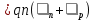 q=1.6 × 10-19 Кл. Для Si: 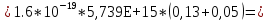 0,00016 См/м 0,00016 См/мДля Ge: 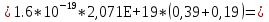 1,9 См/м 1,9 См/мДля SiC: 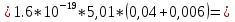 3,69E-20 См/м 3,69E-20 См/мДля InSb: 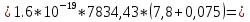 18309,31 См/м 18309,31 См/м5. Сравним полученные в результате расчетов значения γi со своими экспериментальными данными γэксп: Для Si:  эксп >> эксп >>  i , следовательно наблюдается только примесная проводимость i , следовательно наблюдается только примесная проводимостьДля Ge:  эксп >> эксп >>  i , следовательно наблюдается только примесная проводимость i , следовательно наблюдается только примесная проводимостьДля SiC:  эксп >> эксп >>  i , следовательно наблюдается только примесная проводимость i , следовательно наблюдается только примесная проводимостьДля InSb:  эксп > эксп >  i , следовательно наблюдается собственная проводимость i , следовательно наблюдается собственная проводимостьОценим, все ли примеси ионизированы в исследованном температурном интервале или нет. Для этого необходимо сравнить энергию ионизации примеси ∆Эпр с энергией тепловой генерации kTmax. k*Tmax(эВ)=0,0272 Для Si: k*Tmax 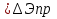 , следовательно не все примеси в полупроводнике ионизированы. , следовательно не все примеси в полупроводнике ионизированы.Для Ge: k*Tmax 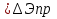 , следовательно не все примеси в полупроводнике ионизированы. , следовательно не все примеси в полупроводнике ионизированы.Для SiC: k*Tmax 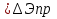 , следовательно не все примеси в полупроводнике ионизированы. , следовательно не все примеси в полупроводнике ионизированы.Для InSb: k*Tmax 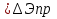 , следовательно не все примеси в полупроводнике ионизированы. , следовательно не все примеси в полупроводнике ионизированы.6.Если в полупроводнике не все примеси ионизированы, то по наклону кривой эксп ln (1/T ) можно найти ∆Эпр: Как видно из графиков ∆Эпр для Si и Ge рассчитать невозможно, т.к. график приближается к асимптоте. Рассчитаем значения эксп n по формуле при T1=298 К, T2=318 К: 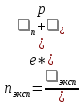 Для SiC: 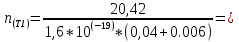 2,77E+21 м-3 2,77E+21 м-3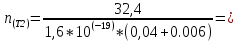 4,4E+21 м-3 4,4E+21 м-3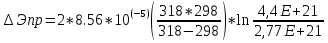 = 0,37 эВ = 0,37 эВДля InSb: 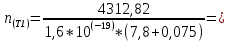 3,4E+21 м-3 3,4E+21 м-3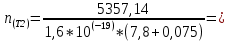 4,24E+21 м-3 4,24E+21 м-3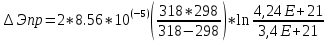 = 0,17 эВ = 0,17 эВ7. Для полупроводников, у которых γэксп ≈ γi, определить ∆Э по формуле: 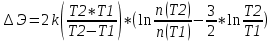 Для InSb: 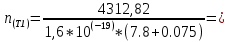 3,4E+21 м-3 3,4E+21 м-3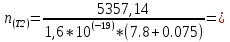 4,24E+21 м-3 4,24E+21 м-3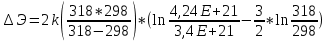 = 0,097 эВ = 0,097 эВВЫВОД: Построенный график (рис. 1) дает понятие о температурной зависимости различных областей проводимости полупроводников. У Ge наблюдается яркий переход от области истощения примесей к области собственной электропроводности. Si находится у порога собственной электропроводности , что соответствует достаточно высокому содержанию примесей. SiC находится в области ионизации примесей на всем температурном диапазоное, что соответствует достаточно высокой энергии ионизации примесей и большой ширине запрещенной зоны. График InSb не имеет четких границ , на нем наблюдается 2 промежутка возрастания проводимости – в области низких и в области высоких температур. Во всех четырех веществах , достаточно высока концентрация доноров, что говорит о том , что все образцы являются примесными полупроводниками. По концентрации можно судить о невыорожденности полупроводников. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
