ALGO_LAB2_17_1362_Римвен Н П. Отчет по лабораторной работе 2 по дисциплине Алгоритмы поиска в линейных структурах данных Тема алгоритмы сортировки массивов Студент гр. 1362 Римвен Н. П
 Скачать 91.93 Kb. Скачать 91.93 Kb.
|
МИНОБРНАУКИ РОССИИСАНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ ЭЛЕКТРОТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ «ЛЭТИ» ИМ. В.И. УЛЬЯНОВА (ЛЕНИНА)Кафедра информационной безопасности ОТЧЕТпо лабораторной работе № 2 по дисциплине «Алгоритмы поиска в линейных структурах данных» Тема: алгоритмы сортировки массивов
Санкт-Петербург 2022 ТЕОРЕТИЧЕСКАЯ ЧАСТЬПоиск определенных значений (ключей) среди элементов линейных структур данных широко используется при создании каталогов, баз данных и т.д. Чаще всего поиск осуществляется в массивах записей, каждая из которых содержит несколько полей (столбцов), при этом зачастую быстрый поиск необходим в разные моменты времени по разным столбцам. Как следствие, система хранения должна обеспечивать возможность быстрого поиска информации по разным столбцам одновременно. Двоичныйпоиск. Этот поиск применяется, если данные в анализируемом списке упорядочены по неубыванию или невозрастанию. В этом случае возможен эффективный поиск с оценкой сложности O(log2n) следующим способом. Для этого поиска вводятся два индекса L и R, в начале они будут обозначать левый и правый конец массива и постепенно будут сдвигаться, сужая область поиска. Далее в цикле вычисляем индекс M, который равен среднему от L и R. Предположим массив отсортирован по возрастанию. Потом мы сравниваем элемент под индексом M с искомым. Если он равен искомому, поиск завершается. Если больше искомого, то правая граница смещается на индекс M-1, так как сам элемент M уже проверен. Если меньше искомого, то левая граница смещается на индекс M+1, так как сам элемент M уже проверен. Дан массив, в нем надо найти число 6: {3, 3, 4, 5, 5, 6, 6, 10, 11, 13, 13, 14, 15, 15, 15} L = 0(3) R = 14(15) M = 7 На первой итерации будет вычислено М, оно равно 7=(0+14)/2. Элемент под индексом равен 10. Следовательно, мы смещаем правую границу на индекс 7, так как 6<10. Далее алгоритм будет работать так: {3, 3, 4, 5, 5, 6, 6, 10, 11, 13, 13, 14, 15, 15, 15} {3, 3, 4, 5, 5, 6, 6, 10, 11, 13, 13, 14, 15, 15, 15} Элемент равный 6 найден, алгоритм поиска закончен. Двоичноедерево. Это вспомогательная структура в виде дерева, каждый узел которого содержит значение узлового элемента и три ссылки: на «левое» поддерево, в котором находятся все элементы, строго меньшие текущего; на «правое» поддерево, в котором находятся все элементы, строго большие текущего; на цепочку ссылок (например, индексов записей в массиве), равных текущей. Поиск осуществляется путем прохождения от корня дерева до искомого элемента, переходом по соответсвенным веткам. Дан массив, в нем надо найти число 6, используя двоичное дерево: {6, 15, 13, 10, 15, 4, 13, 6, 5, 5, 14, 3, 15, 3, 11} Двоичное дерево будет выглядеть так, если мы будем идти от начала массива, поочередно занося значения в дерево:  Чтобы найти число 6, мы берем корень дерева, но он уже является числом 6, поэтому выберем другое число для поиска, например 5. Оно меньше 6, поэтому мы идем в левую ветку. Сравниваем 5 и 4, искомое число больше 4, поэтому идем в правую ветку и сравниваем искомое число со значением, которое там хранится. Там хранится число 5, поэтому поиск завершен. ПРАКТИЧЕСКАЯ ЧАСТЬ Рисунок 1 – Статистика по структуре дерева 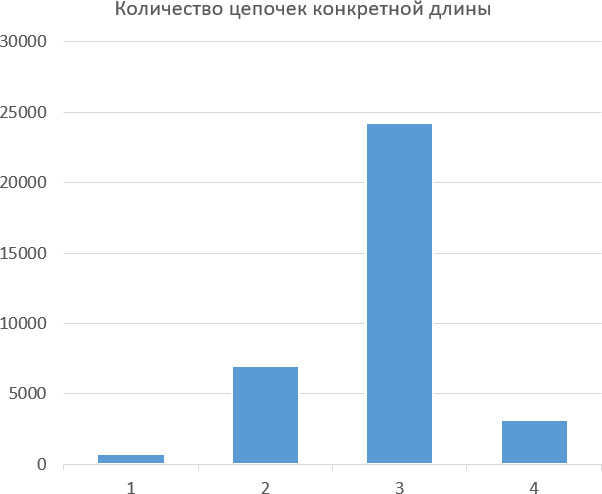 Рисунок 2 – Статистика по структуре таблицы ПРИЛОЖЕНИЕ 1. СТАТИСТИКА В ВИДЕ ЧИСЕЛСтатистика по структуре дерева:
Статистика по структуре хэш-таблицы:
ПРИЛОЖЕНИЕ 2. ИСКОДНЫЙ КОД ПРОГРАММЫФайл с кодом двоичного поиска: int binSearch(int* mass, int num, int size) { size_t L, R, M; L = 0; R = size - 1; while (L <= R) { M = (L+R)/2; if (num < mass[M]) R = M - 1; else if (num > mass[M]) L = M + 1; else { %d", mass[M]); } } printf("\nsuccess!!!\nSearched num: return 0; printf("\nfail, no such number"); return 1; } Файл с кодом бинарного дерева: #include typedef struct ArticulPriceCode { int articul; float price; int code; } APC; typedef struct binaryTree {
APC* data; }tree; int initAPC(APC* apc, int articul, float price, int code) { apc->articul = articul; apc->price = price; apc->code = code; return 0; } int printAPC(APC apc) { printf("\nArticul: %d\nPrice: %.2f\nCode: %d\n", apc.articul, apc.price, apc.code); return 0; } int initTree(tree* Tree, APC firstData) { Tree->left = NULL; Tree->right = NULL; Tree->parent = NULL; Tree->dataAmount = 0; Tree->data = (APC*) malloc(sizeof(APC) * ((Tree- >dataAmount)+1)); Tree->data[Tree->dataAmount] = firstData; return 0; } int addNewData(tree* Tree, APC Data) { size_t i, oldAmount; oldAmount = Tree->dataAmount; APC* oldData = (APC*)malloc(sizeof(APC) * (oldAmount+1)); for(i = 0; i { oldData[i] = Tree->data[i]; } free(Tree->data); Tree->dataAmount = oldAmount+1; Tree->data = (APC*) malloc(sizeof(APC) * (oldAmount+2)); for(i = 0; i { Tree->data[i] = oldData[i]; } Tree->data[oldAmount+1] = Data; return 0; } int addNewTree(tree* firstTree, APC newData) { tree* parentTree = firstTree; tree* tmpTree; while(newData.price != parentTree- >data[0].price) { if(newData.price < parentTree- >data[0].price) { if(parentTree->left == NULL) { tree* newTree = malloc(sizeof(tree)); initTree(newTree, newData); parentTree->left = newTree; newTree->parent = parentTree; return 0; } else { tmpTree = parentTree->left; parentTree = tmpTree; } } else { if(parentTree->right == NULL) { tree* newTree = malloc(sizeof(tree)); initTree(newTree, newData); parentTree->right = newTree; newTree->parent = parentTree; return 0; } else { tmpTree = parentTree->right; parentTree = tmpTree; } } } addNewData(parentTree, newData); return 0; } int searchData(tree firstTree, float searchPrice) { tree searchTree = firstTree; tree* tmpTree; size_t i, amount; while((((int)(searchPrice*100)) - ((int)(searchTree.data[0].price*100))) != 0) { if(((searchTree.left == NULL) && ((searchPrice - searchTree.data[0].price) < 0)) || (((searchPrice - searchTree.data[0].price) > 0) && (searchTree.right == NULL))) { } else { printf("fail, no such number"); return 1; if((searchPrice - searchTree.data[0].price) < 0) { tmpTree = searchTree.left; searchTree = *tmpTree; } else { tmpTree = searchTree.right; searchTree = *tmpTree; } } } printf("success!!!\n"); amount = searchTree.dataAmount; for(i = 0;i { printAPC(searchTree.data[i]); } return 0; } int getStatisticsMas(size_t* mas, tree* firstTree) { size_t depth = 0; tree* presentTree = firstTree; tree* tmpTree; while((firstTree->left != NULL) || (firstTree- >right != NULL)) { if(presentTree->left != NULL) { presentTree = presentTree->left; depth += 1; } else if(presentTree->right != NULL) { } else { presentTree = presentTree->right; depth += 1; mas[depth] += 1; tmpTree = presentTree->parent; if(presentTree->data[0].price < presentTree->parent->data[0].price) { presentTree->parent->left = NULL; } else { presentTree->parent->right = NULL; } free(presentTree); presentTree = tmpTree; depth -= 1; } } return 0; } int main() { float searchPrice, price; int articul, code; size_t stat[100000] = {0}; size_t i; FILE* f = fopen("DATA.txt", "r"); tree zeroTree; APC zeroAPC; fscanf(f, "%d", &articul); fscanf(f, "%f", &price); fscanf(f, "%d", &code); initAPC(&zeroAPC, articul, price, code); initTree(&zeroTree, zeroAPC); while(feof(f) == 0) { APC* newAPC = (APC*) malloc(sizeof(APC));
initAPC(newAPC, articul, price, code); addNewTree(&zeroTree, *newAPC); } fclose(f); printf("search price: "); scanf("%f", &searchPrice); searchData(zeroTree, searchPrice); FILE* statisics = fopen("STAT.txt", "w"); for(i = 0;i<10;i++) { stat[i] = 0; } getStatisticsMas(stat, &zeroTree); for(i = 0;i<100000;i++) { if(stat[i] != 0) { fprintf(statisics, "%zu\t%zu\n", i, stat[i]); } } fclose(statisics); return 0; } Файл с кодом хэш-таблицы: #include #define HEIGH 35129 #define LEN 100000 typedef struct ArticulPriceCode { int articul; float price; int code; } APC; int initAPC(APC* apc, int articul, float price, int code) { apc->articul = articul; apc->price = price; apc->code = code; return 0; } int printAPC(APC apc) { printf("\nArticul: %d\nPrice: %.2f\nCode: %d\n", apc.articul, apc.price, apc.code); return 0; } typedef struct ArrayOfData { size_t dataAmount; APC* data; } AOD; int initAOD(AOD* aod, APC firstData) { aod->dataAmount = 1; aod->data = (APC*)malloc(sizeof(APC)); aod->data[0] = firstData; return 0; } int addDataToAOD(AOD* aod, APC newData) { APC* oldData = (APC*)malloc(sizeof(APC) * aod- >dataAmount); for(size_t i = 0; i < aod->dataAmount;i++) { oldData[i] = aod->data[i]; } free(aod->data); aod->dataAmount += 1; aod->data = (APC*)malloc(sizeof(APC) * aod- >dataAmount); for(size_t i = 0; i < aod->dataAmount-1;i++) { aod->data[i] = oldData[i]; } aod->data[aod->dataAmount-1] = newData; return 0; } int addNewData(AOD* hashTable, APC newData) { size_t result = newData.articul % HEIGH; if(hashTable[result].data == NULL) { initAOD(&hashTable[result], newData); } else { addDataToAOD(&hashTable[result], newData); } return 0; } int initTable(AOD* hashTable) { for(size_t i = 0;i { hashTable[i].dataAmount = 0; hashTable[i].data = NULL; } return 0; } int searchInHash(AOD* hashTable, int searchArticul) { size_t i, amount, result = searchArticul % HEIGH; if(hashTable[result].data == NULL) { printf("\nfail, no such articul"); return 1; } else { amount = hashTable[result].dataAmount; for(i = 0; i< amount; i++) { searchArticul) if(hashTable[result].data[i].articul == { printf("\nsuccess!!!"); printAPC(hashTable[result].data[i]); return 0; } } } printf("\nfail, no such articul"); return 1; } int getStatisticsMas(AOD* hashTable, size_t* mas) { size_t i; for(i = 0;i { mas[i] = 0; } for(i = 0;i { if(hashTable[i].data != NULL) { mas[hashTable[i].dataAmount] += 1; } } return 0; } int main() { AOD* hashTable; size_t stat[LEN]; size_t i, summ = 0; FILE* f = fopen("DATA.txt", "r"); int articul, code, searchedArticul; float price; hashTable = (AOD*)malloc(sizeof(AOD) * HEIGH); initTable(hashTable); while(feof(f) == 0) { APC newAPC; fscanf(f, "%d", &articul); fscanf(f, "%f", &price); fscanf(f, "%d", &code); initAPC(&newAPC, articul, price, code); addNewData(hashTable, newAPC); } fclose(f); printf("Enter articul: "); scanf("%d", &searchedArticul); searchInHash(hashTable, searchedArticul); FILE* statisics = fopen("STAT.txt", "w"); getStatisticsMas(hashTable, stat); for(i = 0;i { if(stat[i] != 0) { fprintf(statisics, "%zu\t%zu\n", i, stat[i]); } } fclose(statisics); return 0; } ВЫВОДЫБыли изучены и реализованы в программном коде алгоритмы поиска: двоичный алгоритм, алгоритм, использующий бинарное дерево, алгоритм, использующий хэш-таблицу. Также была собрана статистика по двум последним алгоритмам и оформлена в виде гистограммы. |
