Методы_оптимизации,_Лаба_№_2,_Суслов_М_В_,_ПИ_310з. Отчет по лабораторной работе 2 Решение транспортной задачи методами северозападного угла и минимального элемента
 Скачать 28.36 Kb. Скачать 28.36 Kb.
|
|
ФГБОУ ВО Уфимский Государственный Авиационный Технический Университет Кафедра АСУ Отчет по лабораторной работе №2 «Решение транспортной задачи методами северо-западного угла и минимального элемента» по дисциплине «Методы оптимизации»Вариант №13Выполнил: ст. гр. ПИ-310з Данилкин А.И. Проверил: старший преподаватель Кондратьева О.В. Уфа 2022 Условие задачи Три предприятия данного экономического района могут производить некоторую однородную продукцию в количествах соответственно равных А1 = 120, А2 = 310, А3 = 120 единиц. Эта продукция должна быть поставлена пяти потребителям в количествах, соответственно равных В1 = 110, В2 = 110, В3 = 100 В4 = 120, В5 = 110 единиц. Затраты, связанные с производством и доставкой единицы продукции, задаются матрицей С. 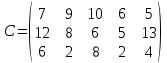 Составить план прикрепления потребителей к поставщикам, решить задачу двумя методами (северо-западный угол, минимального элемента), сделать вывод о том, какой из используемых методов является наиболее выгодным. Вычисление методом северо-западного угла Составим таблицу с данными по задаче.
У нас 3 пункта отправления и 5 пунктов назначения. Следовательно, опорный план задачи определяется числами, стоящими в 3 + 5 – 1 = 7 заполненных клетках. Начнем пошагово заполнять эту таблицу данными по перевозкам. Согласно методу северо-западного угла, мы всегда выбираем левый верхний угол таблицы. Мысленно вычеркиваем строки и столбцы по мере заполнения пунктов назначения и опустошения пунктов отправления. Шаг 1. Перевозим 120 ед. товара из 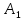 в в 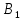 . .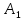 пуст. Вычеркиваем строку пуст. Вычеркиваем строку 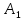 . .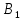 имеет еще место для 110 ед. товара. имеет еще место для 110 ед. товара.Шаг 2. Перевозим 70 ед. товара из 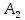 в в 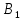 . .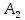 хранит еще 200 ед. товара. хранит еще 200 ед. товара.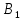 полон. Вычеркиваем столбец полон. Вычеркиваем столбец 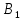 . .Шаг 3. Перевозим 80 ед. товара из 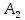 в в 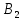 . .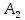 хранит еще 120 ед. товара. хранит еще 120 ед. товара.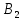 полон. Вычеркиваем столбец полон. Вычеркиваем столбец 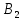 . .Шаг 4. Перевозим 120 ед. товара из 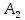 в в 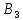 . .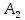 пуст. Вычеркиваем строку пуст. Вычеркиваем строку 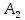 . .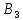 имеет еще место для 10 ед. товара. имеет еще место для 10 ед. товара.Шаг 5. Перевозим 10 ед. товара из 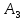 в в 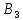 . .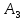 хранит еще 100 ед. товара. хранит еще 100 ед. товара.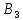 полон. Вычеркиваем столбец полон. Вычеркиваем столбец 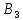 . .Шаг 6. Перевозим 70 ед. товара из 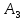 в в 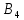 . .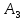 хранит еще 30 ед. товара. хранит еще 30 ед. товара.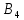 полон. Вычеркиваем столбец полон. Вычеркиваем столбец 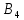 . .Шаг 6. Перевозим 30 ед. товара из 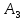 в в 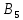 . .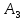 пуст. пуст.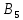 полон. полон.В результате выполнения шагов получаем:
Результат решения методом северо-западного угла Опорный план: 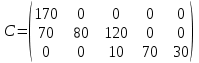 Помножив количество грузов на тарифы получаем общую стоимость перевозок: 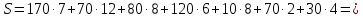 3730 3730Вычисление методом минимального элемента. Возьмем таблицу с данными по задаче, составленную в предыдущем методе. Добавим в нее тарифы по перевозкам.
Как и в предыдущем методе, опорный план задачи определяется числами, стоящими в 7 заполненных клетках. Начнем пошагово заполнять эту таблицу данными по перевозкам. Согласно методу минимального элемента, мы всегда выбираем клетку с самым дешевым тарифом. Мысленно вычеркиваем строки и столбцы по мере заполнения пунктов назначения и опустошения пунктов отправления. Шаг 1. Самый дешевый тариф 2 находится в клетках 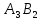 и и 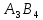 . Выбираем произвольную клетку. Пусть это будет . Выбираем произвольную клетку. Пусть это будет 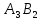 . .Перевозим 80 ед. товара из 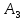 в в 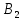 . .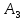 имеет еще место для 30 ед. товара. имеет еще место для 30 ед. товара.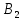 полон. Вычеркиваем столбец полон. Вычеркиваем столбец 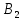 . .Шаг 2. Самый дешевый тариф 2 находится в клетке 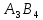 . .Перевозим 30 ед. товара из 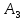 в в 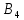 . .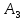 пуст. Вычеркиваем строку пуст. Вычеркиваем строку 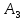 . .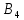 имеет еще место для 40 ед. товара. имеет еще место для 40 ед. товара.Шаг 3. Самый дешевый тариф 5 находится в клетках 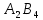 и и 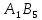 . Выбираем произвольную клетку. Пусть это будет . Выбираем произвольную клетку. Пусть это будет 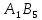 . .Перевозим 30 ед. товара из 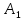 в в 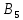 . .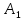 имеет еще место для 140 ед. товара. имеет еще место для 140 ед. товара.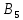 полон. Вычеркиваем столбец полон. Вычеркиваем столбец 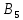 . .Шаг 4. Самый дешевый тариф 5 находится в клетке 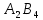 . . Перевозим 40 ед. товара из 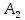 в в 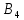 . .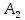 имеет еще место для 140 ед. товара. имеет еще место для 140 ед. товара.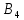 полон. Вычеркиваем столбец полон. Вычеркиваем столбец 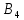 . .Шаг 5. Самый дешевый тариф 6 находится в клетке 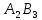 . . Перевозим 130 ед. товара из 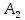 в в 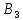 . .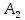 имеет еще место для 140 ед. товара. имеет еще место для 140 ед. товара.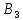 полон. Вычеркиваем столбец полон. Вычеркиваем столбец 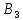 . .Шаг 6. Самый дешевый тариф 7 находится в клетке 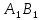 . . Перевозим 140 ед. товара из 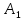 в в 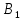 . .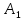 пуст. Вычеркиваем строку пуст. Вычеркиваем строку 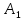 . .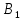 имеет еще место для 100 ед. товара. имеет еще место для 100 ед. товара.Шаг 7. Последний тариф 12 находится в клетке 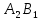 . . Перевозим 100 ед. товара из 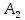 в в 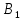 . .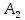 пуст. пуст.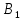 полон. полон.В результате выполнения шагов получаем:
Результат решения методом минимального элемента Опорный план: 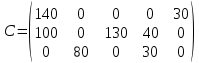 Помножив количество грузов на тарифы получаем общую стоимость перевозок: 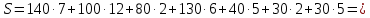 3530 3530Вывод Перевозки, рассчитанные методом минимального элемента (3530), оказались выгоднее перевозок, рассчитанных методом северо-западного угла (3730), на 200. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
