Использование интерференционных колец равного наклона для определения показателя преломления стекла. Отчет по лабораторной работе 3 Использование интерференционных колец равного наклона для определения показателя преломления стекла.
 Скачать 70.86 Kb. Скачать 70.86 Kb.
|
|
Министерство науки и высшего образования Российской федерации Федеральное государственное бюджетное образовательное учреждение высшего образования «Кузбасский государственный технический университет имени Т. Ф. Горбачева» Кафедра физики Отчет Отчетпо лабораторной работе №3 «Использование интерференционных колец равного наклона для определения показателя преломления стекла.» Выполнил ст. группы ХОб-181: Шамин М.В. (Ф.И.О.) Преподаватель: Смирнов В.Г. (Ф.И.О.)
1. Цель работы: получение интерференционной картины методом деления амплитуды и определение показателя преломления стекла. 2. Описание экспериментальной установки: Из лазера 1 (рис. 1) световой пучок падает на короткофокусную линзу 2 и, становясь расходящимся, освещает плоскопараллельную стеклянную пластину 3, находящуюся на подставке оптической скамьи. Отражаясь от передней и задней поверхности стекла, световые волны становятся когерентными и интерферируют между собой. На экране Э, поставленном перед пластиной, наблюдается интерференционная картина (ИК) в виде чередующихся светлых и темных колец, называемых полосами равного наклона. 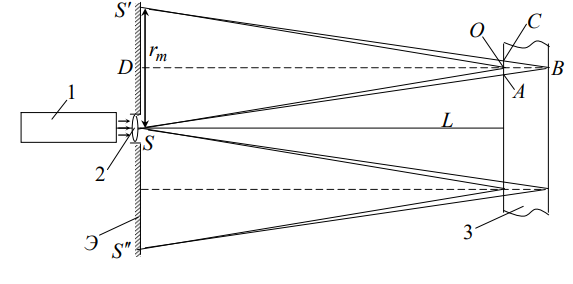 Рис. 1. Схема получения интерференционной картины: А, О, С – точки пересечения лучей с передней гранью пластины; B – точка пересечения лучей с задней гранью пластины; S – задний фокус линзы; S, S – точки, лежащие на темном кольце радиуса 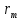 . .3. Краткая теория: Оптическая разность хода лучей SABCS и SOS на рис. 2 равна 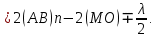 Здесь n – показатель преломления; 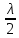 – скачок разности хода при отражении луча SO от оптически более плотной среды (стекла). – скачок разности хода при отражении луча SO от оптически более плотной среды (стекла).Если d – толщина пластины, и – углы падения и преломления, то 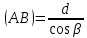 , , 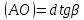 , MO AO , MO AO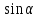 . Используя закон преломления . Используя закон преломления 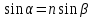 , выражение (1) можно переписать в виде , выражение (1) можно переписать в виде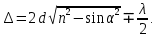 Темные кольца наблюдаются, если разность хода равна 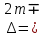 1) 1)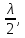 где m 1, 2, 3 … – интерференционный порядок. Таким образом, каждому темному кольцу соответствует свое значение m. Это значение связано с величиной разности оптических путей двух световых волн, результатом интерференции которых является данное кольцо. Сравнивая (2) и (3), условие наблюдения темных колец представим в виде  Используем (4) для получения выражения для радиуса темного кольца. Для центральной части ИК угол падения мал, поэтому можно принять, что sin tg. Используя SOD, и что , получим sin 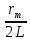 , где L – расстояние от источника S до пластины; , где L – расстояние от источника S до пластины; 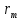 – радиус m-го темного кольца. Преобразуем выражение (4), подставляя приближенное значение sin. Учитывая, что – радиус m-го темного кольца. Преобразуем выражение (4), подставляя приближенное значение sin. Учитывая, что 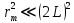 , получим по формуле приближенных вычислений: , получим по формуле приближенных вычислений: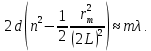 Здесь использовано то, что 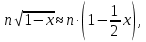 когда когда 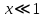 . .Откуда следует: 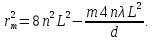 Из рис. 1 и 2 видно, что кольцу большего радиуса соответствует и большее значение угла падения . С увеличением же угла падения , согласно (4), уменьшается интерференционный порядок m кольца. Следовательно, самый большой интерференционный порядок 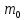 имеет то кольцо, которое находится в центре ИК. Ее центру соответствует 0. При этом угле падения из (4) следует, что имеет то кольцо, которое находится в центре ИК. Ее центру соответствует 0. При этом угле падения из (4) следует, что 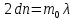 , и в самом центре ИК находится темное кольцо с самым большим номером , и в самом центре ИК находится темное кольцо с самым большим номером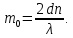 Кроме него в центральном темном пятне скрыты темные кольца с номерами от 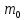 до k , а первое наблюдаемое имеет номер до k , а первое наблюдаемое имеет номер 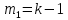 , второе , второе 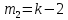 , …, N-е , …, N-е 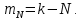 Запишем условие (5) для минимума (k – N)-го порядка 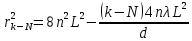 и для минимума k -го порядка 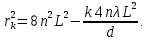 Вычитая уравнение (8) из (7) почленно, получим 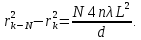 Таким образом, квадрат радиуса кольца линейно зависит от его номера N: 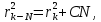 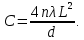 Введем сокращенные обозначения для радиусов темных колец: 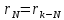 . Тогда (10) примет вид . Тогда (10) примет вид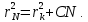 Если результаты измерений радиусов колец представить графически как 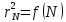 , то по точкам графика, в соответствии с (12), можно провести усредняющую прямую. Используя прямую, можно найти значение С как тангенс угла наклона прямой к оси N: , то по точкам графика, в соответствии с (12), можно провести усредняющую прямую. Используя прямую, можно найти значение С как тангенс угла наклона прямой к оси N: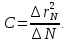 После чего показатель преломления можно определить, используя формулу (11), 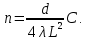 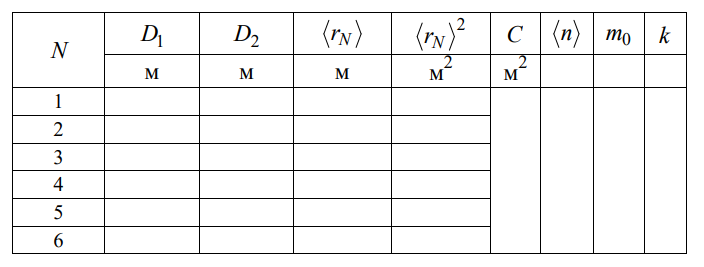 Таблица 1. Результаты измерений диаметров темных колец и полученные значения величин: С, n , 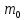 , k. , k. |
