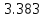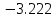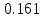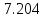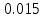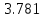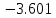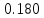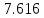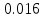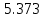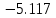Лабораторная 3 аэрология. Лаба3. Отчет по лабораторной работе 3 Определение количества воздуха, поступающего в модель

• Название: Отчет по лабораторной работе 3 Определение количества воздуха, поступающего в модель
• Анкор: Лабораторная 3 аэрология
• Дата: 11.02.2023
• Размер: 203.29 Kb.
• Имя файла: Лаба3.docx
• Тип: Отчет; #931109

Министерство науки и высшего образования

Российской федерации

САНКТ-ПЕТЕРБУРГСКИЙ ГОРНЫЙ УНИВЕРСИТЕТ


Кафедра безопасности производств
ОТЧЕТ

По лабораторной работе №3

Определение количества воздуха, поступающего в модель

Выполнили: студенты гр. ТПР-17

/Савенков А.А./

(подпись) (Ф.И.О.)

Проверил: асс. каф. БП /Кабанов Е.И./

(должность) (подпись) (Ф.И.О.)


Санкт-Петербург

2021

Цель работы: получить опыт использования уравнения Бернулли для решения конкретных задач, научиться определять количество (расход) воздуха, поступающего в коллектор установки, оценить виды сопротивления и депрессии, закрепить навыки работы с измерительными приборами и обработки результатов измерений.
Общие сведения

Участок 0 – 1, на котором производятся измерения статической депрессии, представляет собой коллектор модели, через который воздух из атмосферы лаборатории входит в установку. Уравнение Бернулли для этого участка при отсутствии естественной тяги (h_e =0):

h_{ст 0 -1} + h_{ск 0 -1} = h_{вх 0 – 1} (1)

где h _{ст 0-1} – статическая депрессия на участке 0–1; h _{ск 0-1} – скоростная депрессия на этом же участке; h _{вх 0–1} – депрессия (потеря давления), расходуемая на преодоление сопротивления входа в коллектор установки.

h_{ск 0 - 1}= p_{ск 0} – p_{ск 1} = (v₀₂ - v₁₂) γ / 2g , (2)

где v₀ и v₁ – средние скорости движения воздуха соответственно в атмосфере лаборатории и в коллекторе, где расположена точка 1, м/с; γ – удельный вес воздуха.

Так как v₀ = 0, а v₁>0, то h _{ск 0-1}= - γ v₁₂/ 2g

В соответствии с этим уравнение (1) может быть представлено в виде

h _{ст 0 -1} = h _{вх 0} – 1 + γ v₁₂/ 2g (3)

Физический смысл этих преобразований состоит в следующем. Так как величина h_{ск 0-1} имеет отрицательный знак (разряжение), то она трактуется как сопротивление движению воздуха и по абсолютной величине суммируется с сопротивлением входа h_вх 0–1. Это свидетельствует о том, что энергия давления вентилятора на участке 0–1 (статическая депрессия h_{ст 0 –1}) расходуется не только на преодоление сопротивления входа, но и на «разгон» воздуха со скорости v₀ = 0 в атмосфере до v₁>0 в точке 1.

Между первым и вторым слагаемым в правой части формулы (3) есть существенное различие. Часть энергии давления h_{ст 0–1} , расходуемая на преодоление сопротивления входа (h _{вх 0–1}), безвозвратно теряется, рассеиваясь в форме тепла; другая же ее часть, расходуемая на разгон воздуха (γ v₁₂/ 2g), переходит в кинетическую (скоростную) энергию воздушного потока, т.е. энергия давления переходит в энергию движения.

Энергия, затрачиваемая на преодоление сопротивления входа (вход в коллектор рассматривается как местное сопротивление), пропорциональна скоростной энергии потока, т.е.

h _{вх 0–1} = ξ _к γ v₁₂/ 2g (4)

где ξ_к = 0,05 - безразмерный коэффициент местного сопротивления на входе в коллектор (величина его установлена эмпирически).

Подставив выражение (4) в формулу (3), получим

h_{ст 0-1} = (ξ_к +1) γ v₁₂/ 2g (5)

Из формулы (5) следует, что, измерив статическую депрессию на входе в коллектор h ст 0 –1, можно определить среднюю скорость движения воздуха в коллекторе:

v₁=[( 2g h_{ст 0–1}) / 1,05 γ ]0,5 (6)

Зная среднюю скорость v1 и площадь поперечного сечения коллектора S₁ =0,0021 м², можно определить количество воздуха, поступающего в коллектор модели

Q = v₁S₁ (23)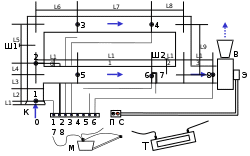



Рисунок 1 – Схема аэродинамической установки

Температура воздуха в лаборатории: t = 22⁰С

Атмосферное давление в лаборатории: p₀ = 103.9 кПа
Результаты исследований

Таблица№1. Результаты измерений

Номер открытого шибера	Участок, на котором производится замер	Вид измеряемой депрессии	Тип измерительного прибора	Фактор прибора Км	Жидкость, используемая в приборе	Показания прибора
						Положение мениска в трубке прибора		Подъем уровня жидкости h п , мм		Величина депрессии h, мм вод. ст.
						Начальное h 0 , мм	Конечное h к , мм
1	0 – 1	h СТ	ММН	0,2	Спирт	18	35		17		3,4
2							37		19		3,8
1 и 2							45		27		5,4

Таблица№2. Результаты вычислений

Номер открытого шибера	h ст 0 –1	h ск 0-1	h вх 0 – 1	v1 , м /c	Q, м3/c
1
2
1 и 2

Ход работы

1. 
   При помощи микроманометра измерены начальное и конечное положения столбов жидкости. Затем вычислен подъем уровня жидкости: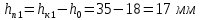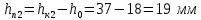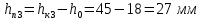
   

2. 
   Затем величина статической депрессии для каждого участка рассчитывается по формуле: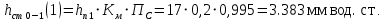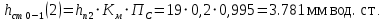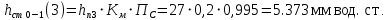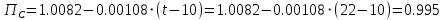
   

3. 
   Средняя скорость движения воздуха в коллекторе:
   

4. 
   Количество воздуха, поступающего в коллектор модели: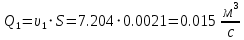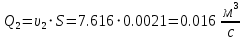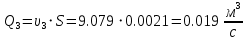
   

;

;

.

где S=0.0021 м² – площадь поперечного сечения коллектора

5. 
   Скоростная депрессия на этом же участке:
   

h_{ск 0 - 1}= - v₁² γ /2g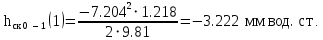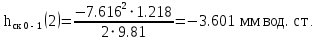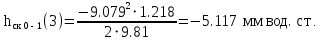

6. 
   Депрессия (потеря давления), расходуемая на преодоление сопротивления входа в коллектор установки:
   

h_{вх 0 – 1} = ξ_к γ v₁²/ 2g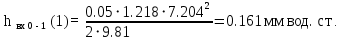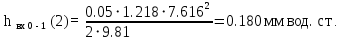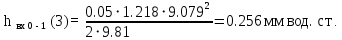







где ξ_к=0.05 - безразмерный коэффициент местного сопротивления на входе в коллектор (величина его установлена эмпирически).

7. 
   По результатам рассчитанных депрессий выполняется проверка на правильность измерений, проделанных с помощью микроманометром: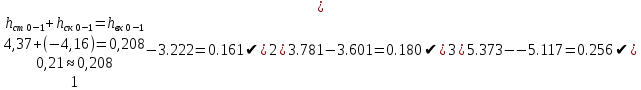
   

Погрешность измерений не выходит за предел ±2 мм, следовательно, измерения выполнены правильно.

Вывод: в данной лабораторной работе был произведен расчет средней скорости движения воздуха в коллекторе, количества воздуха поступающего в коллектор установки, статической, скоростной, а также депрессии расходуемой на преодоление сопротивления входа в коллектор установки.