Алексеев_работа_4. Отчет по лабораторной работе 4 Линейные дискретные системы Алексеев Н. С. группа бпо2002 Проверил

• Название: Отчет по лабораторной работе 4 Линейные дискретные системы Алексеев Н. С. группа бпо2002 Проверил
• Дата: 10.11.2022
• Размер: 5.11 Mb.
• Имя файла: Алексеев_работа_4.docx
• Тип: Отчет; #781384

Импульсные системы

Отчет по лабораторной работе № 4

Линейные дискретные системы

Выполнил: Алексеев Н.С. группа БПО-20-02

Проверил:

Преподаватель Черникова М.А.

Вариант

1

Вариант	n2	n1	n0	d1	d0	a1	a2	c1	c2
	2.7	-1.6	-0.3	-0.8	0.12	0.74	-0.33	0.30	0.33

1. 
   Исследование разомкнутой дискретной системы
   

Передаточная функция системы:

F(z)= -0.3 -1.6z +2.7z²

-----------------

0.12 -0.8z +z²

Реакция системы на единичный ступенчатый входной сигнал при нулевых начальных условиях: 

v[0]  = 2.7 v[1]  = 6.46 v[2]  = 8.844

v[3]  = 9.9768 v[4]  = 10.92016

Нули передаточной функции: 

z = 0.7422813 + 0.i

-0.1496887 + 0.i

Полюса  передаточной функции: 

p = 0.6 + 0.i

0.2 + 0.i

Устойчивость: 

Система устойчива, т.к. существует коэффициент усиления звена в установившемся режиме

Z-преобразование входного сигнала e₁[k]: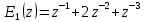



Z-преобразование входного сигнала e₂[k]: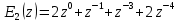



Результаты моделирования системы при входах e1 (v1), e2 (v3), e1+e2 (v) и 0,5(e1+e2) (v3):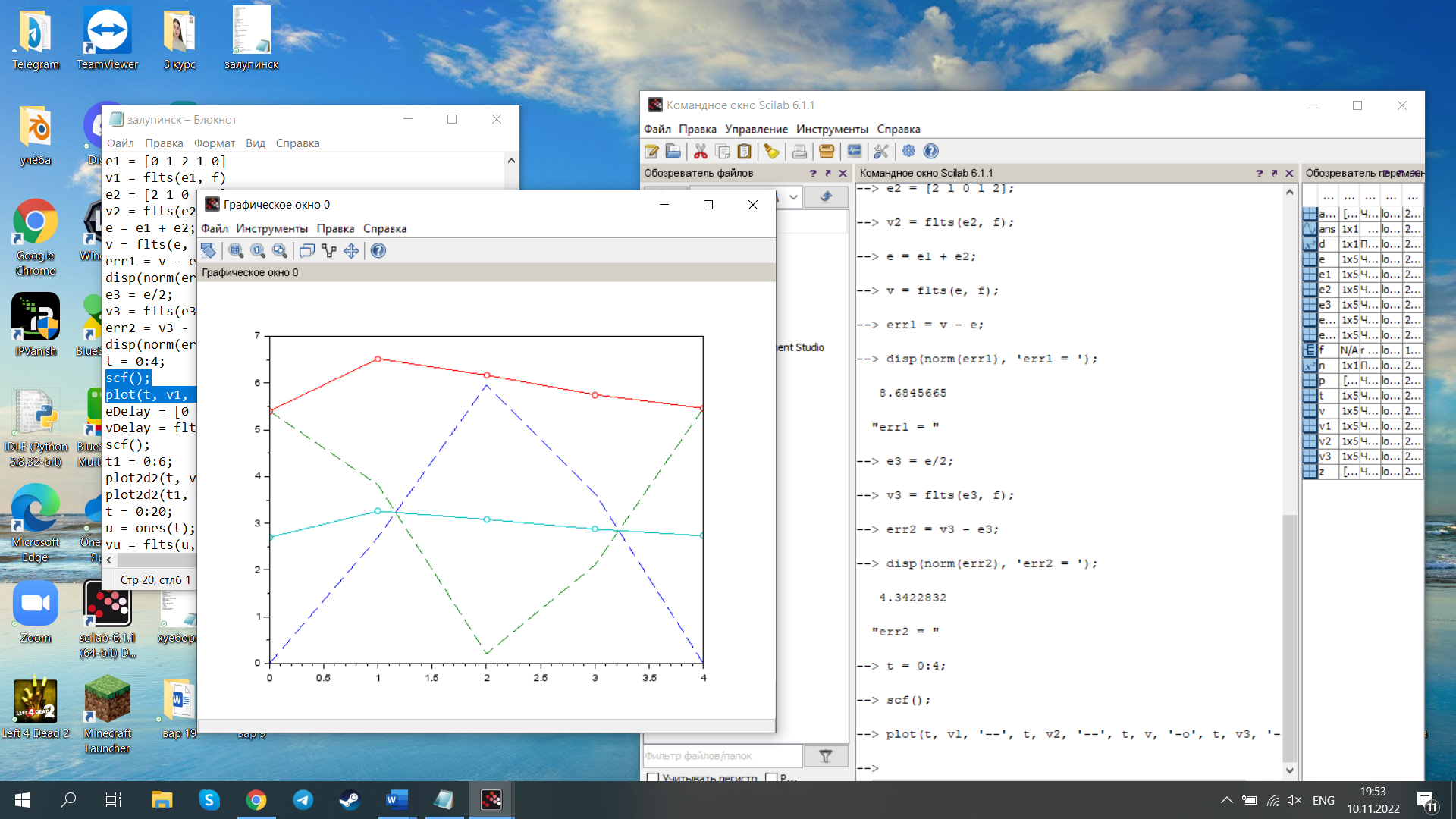



Выводы:

Свойство однородности выполняется, потому что умножение входного сигнала на постоянную приводит к умножению выходного сигнала на ту же постоянную.

Свойство суперпозиции (аддитивности) выполняется, потому что реакция на сумму сигналов равна сумме реакций этой системы на отдельные сигналы.

Z-преобразование сигнала e[k] = e₁[k] + e₂[k]:

E(z) = 2z⁰+2z^-1+2z^-2+2z^-3+2z^-4

Z-преобразование сигнала e₃[k] = 0,5·e[k]:

E₃(z) = z⁰+z^-1+z^-2+z^-3+z^-4

Z-преобразование запаздывающего сигнала e_delay[k] = e[k-2]:

E_delay(z) = 2z^-2+2z^-3+2z^-4+2z^-5+2z^-6

Реакция на запаздывающий сигнал e_delay[k]: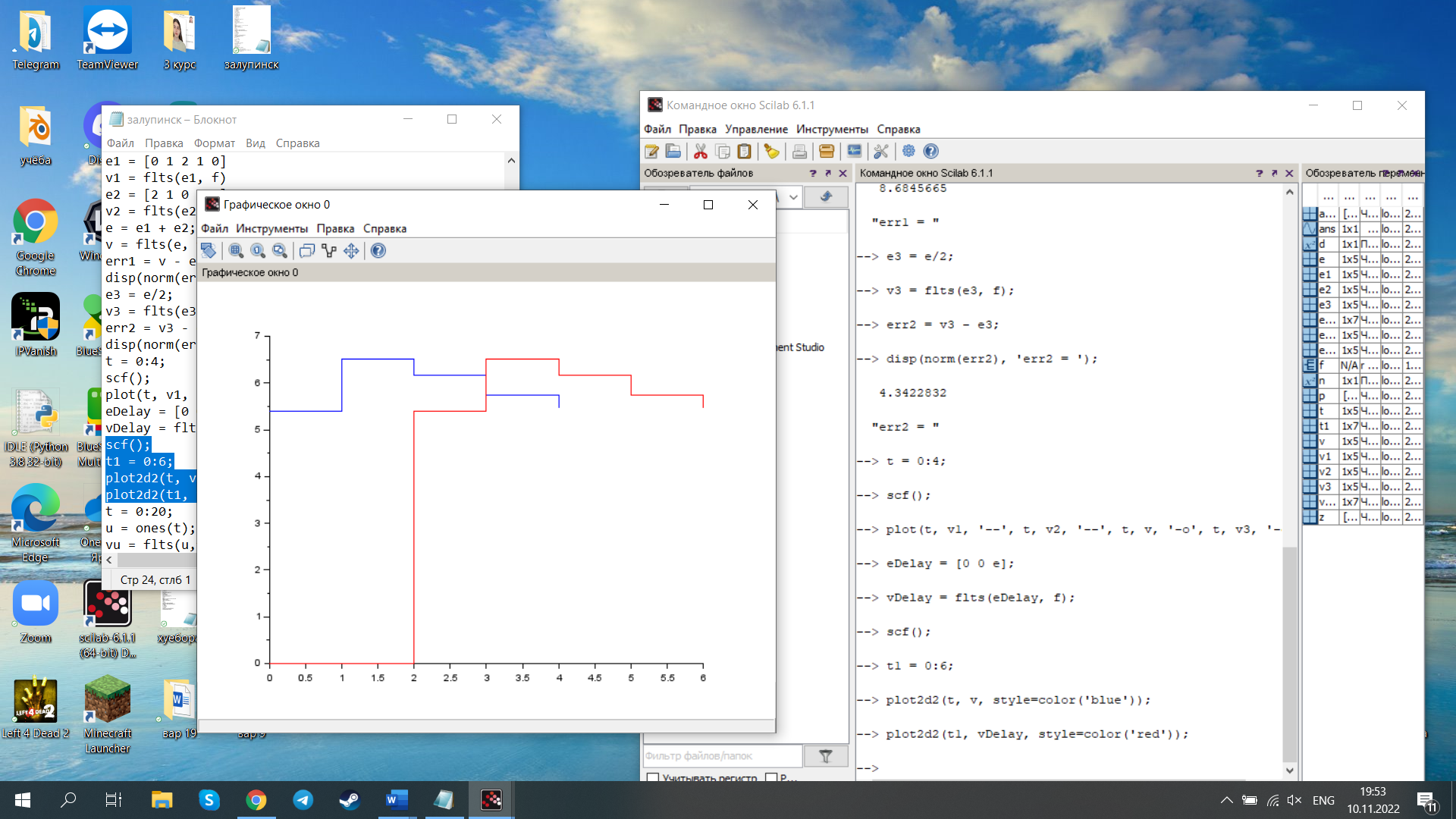  



Выводы: 

условие стационарности выполняется, потому что запаздывающий сигнал в точности повторяет значения исходного сигнала

z-преобразование единичного ступенчатого сигнала u[k]:

U(z) =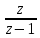

z -преобразование сигнала выхода системы v[k] при входе u[k]:

V(z) =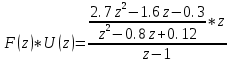

Начальное и конечное значения выходного сигнала (теоретически):

v[0] = a₂ = 2.7;

v[∞] = 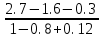= 3.343;

Реакция системы на единичный ступенчатый сигнал: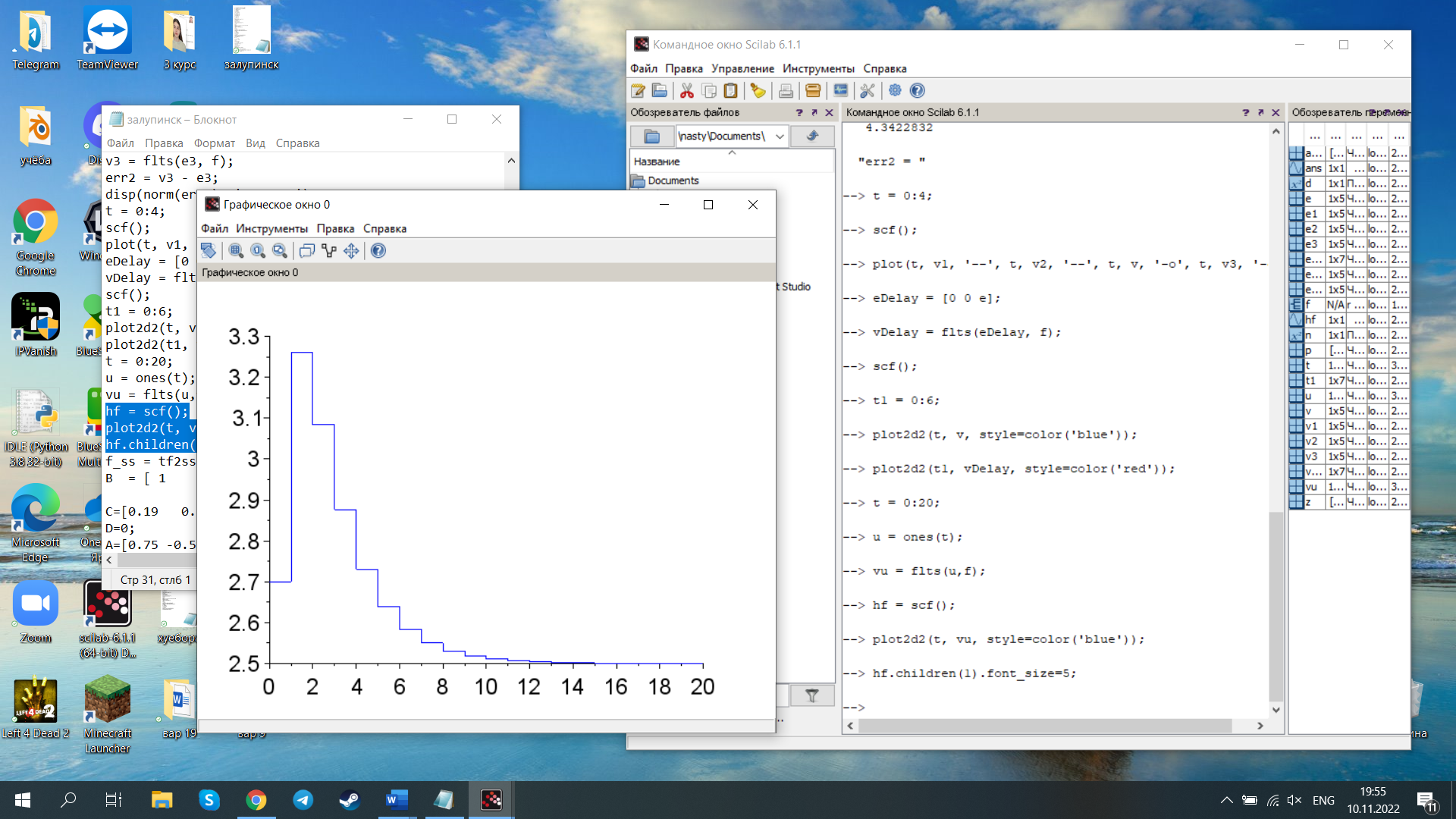



Выводы:

Теоретические расчёты подтверждаются моделированием.

2. 
   Исследование дискретной модели в пространстве состояний
   

Модель в пространстве состояний:

A = [ 0.74 -0.33

1 0 ];

B = [ 1

0];

C = [ 0.30 0.33];

D = 0.

Собственные числа матрицы A: 

0.377 + 0.4334409i

0.377 - 0.4334409i

Устойчивость: 

Система устойчива, потому что модули собственных чисел меньше 1.

Импульсная характеристика: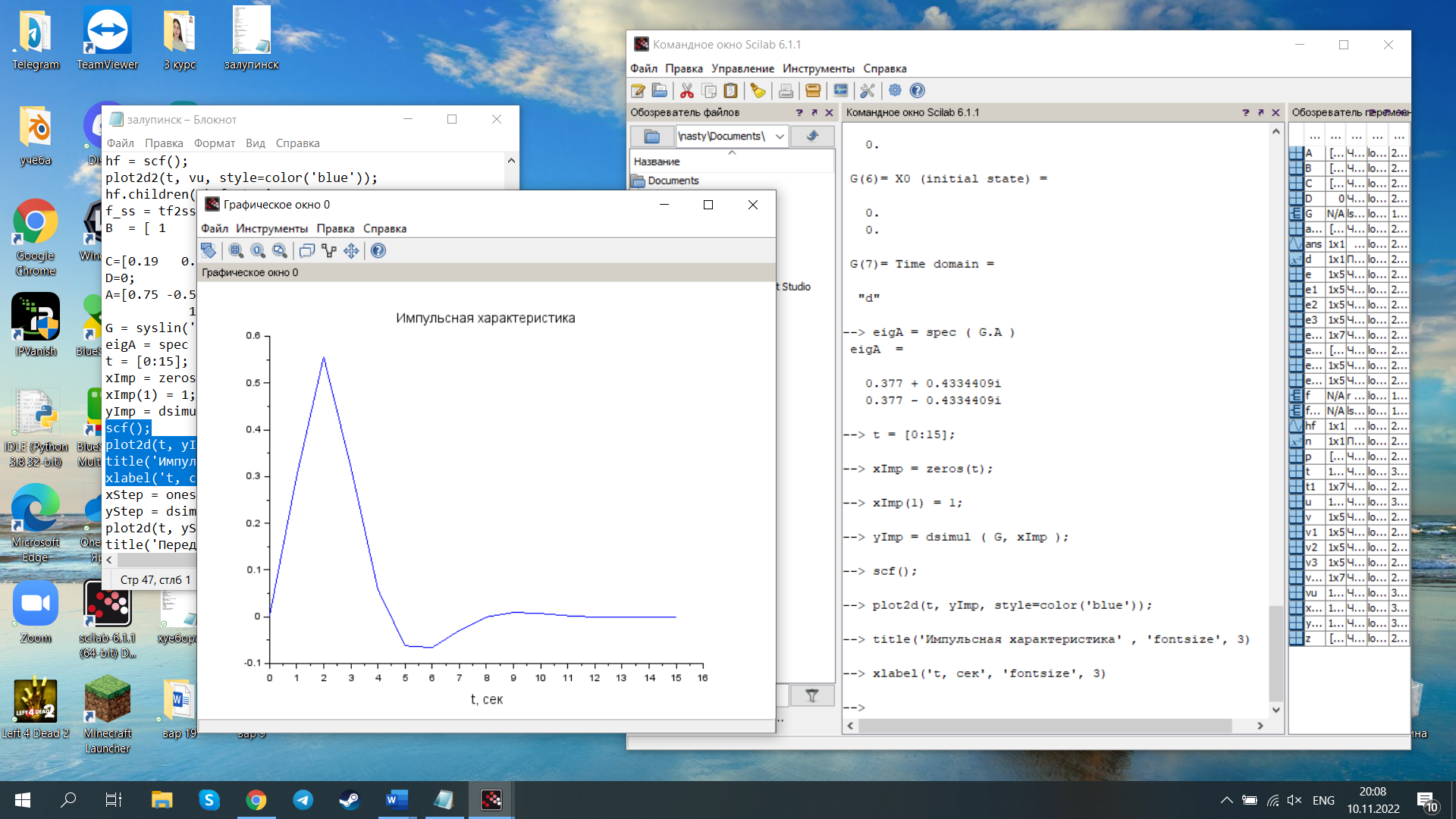 



Переходная  характеристика: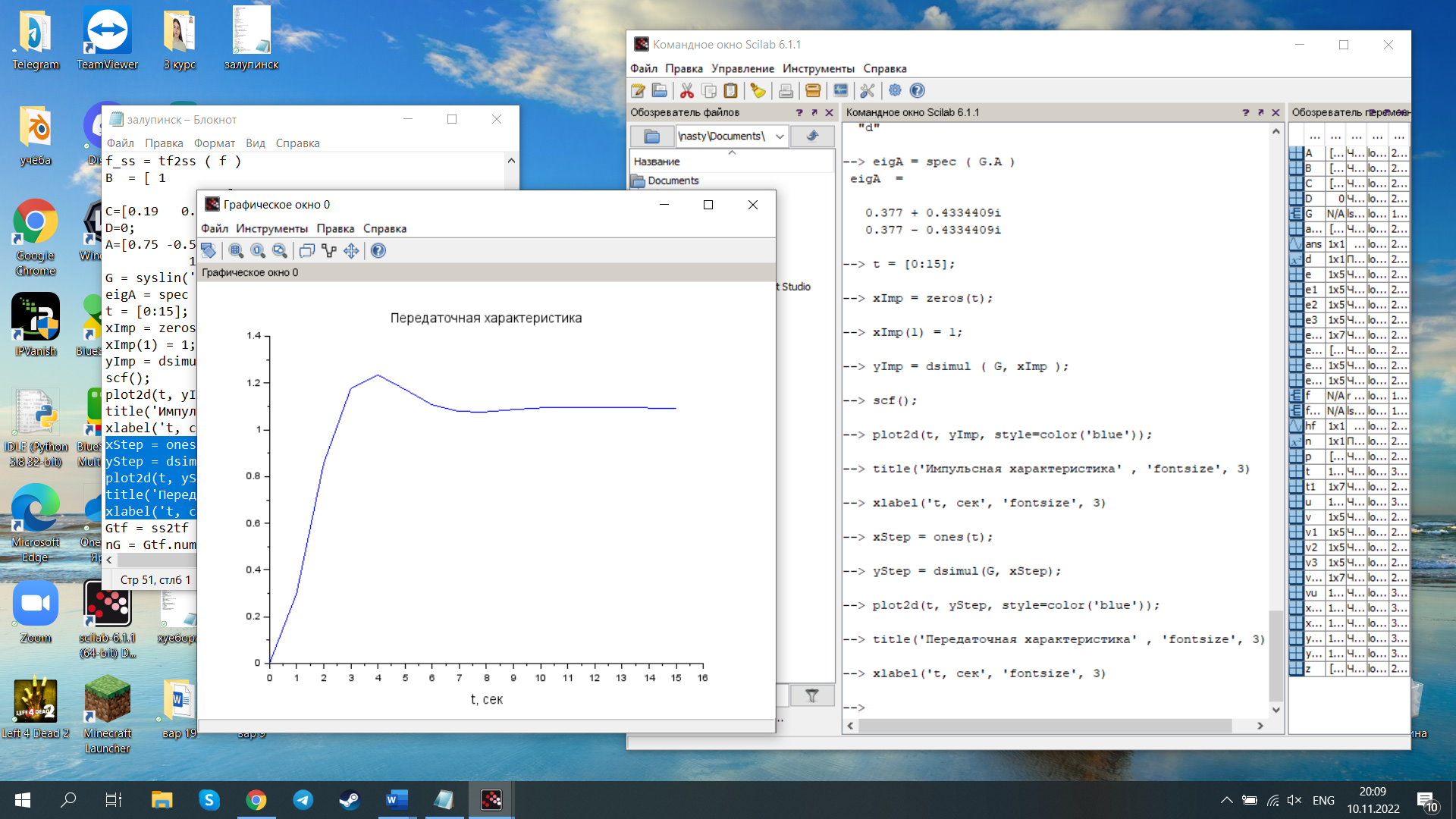 



Передаточная функция: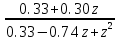 

 


Полюса передаточной функции: 

0.377 + 0.4334409i

0.377 - 0.4334409i

Выводы: 

Система устойчива.

Полюса передаточной функции совпадают с собственными числами матрицы A модели в пространстве состояний.

Обратный переход в пространство состояний: 

A = [ 0.0688356 -0.8114384

0.3485616 0.6851644];

B = [ -0.3284459

0.7225810];

C = [ -0.9133924 0.];

D = 0.

Выводы: 

Модели в пространстве состояний оказались разные, потому что одной системе соответствует бесконечное множество моделей в пространстве состояний.

Статический коэффициент усиления системы: 

k = 1.09375

Выводы: 

Установившееся значение переходной характеристики совпадает с результатами моделирования.

Время переходного процесса: 

t_п = 6

3. 
   Исследование замкнутой системы
   

Передаточная функция регулятора:

 

Структурная схема системы: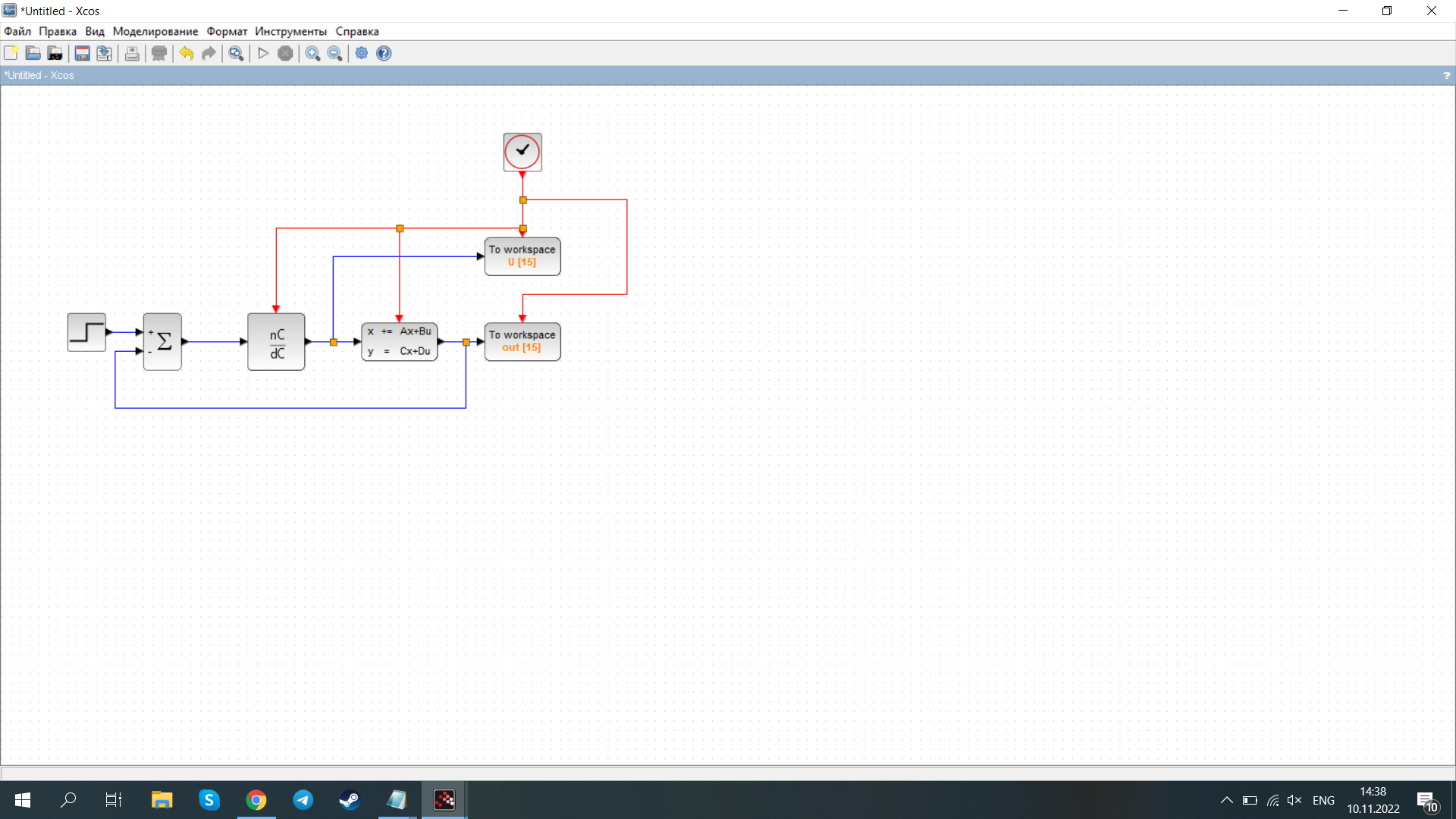



Переходные процессы в системе: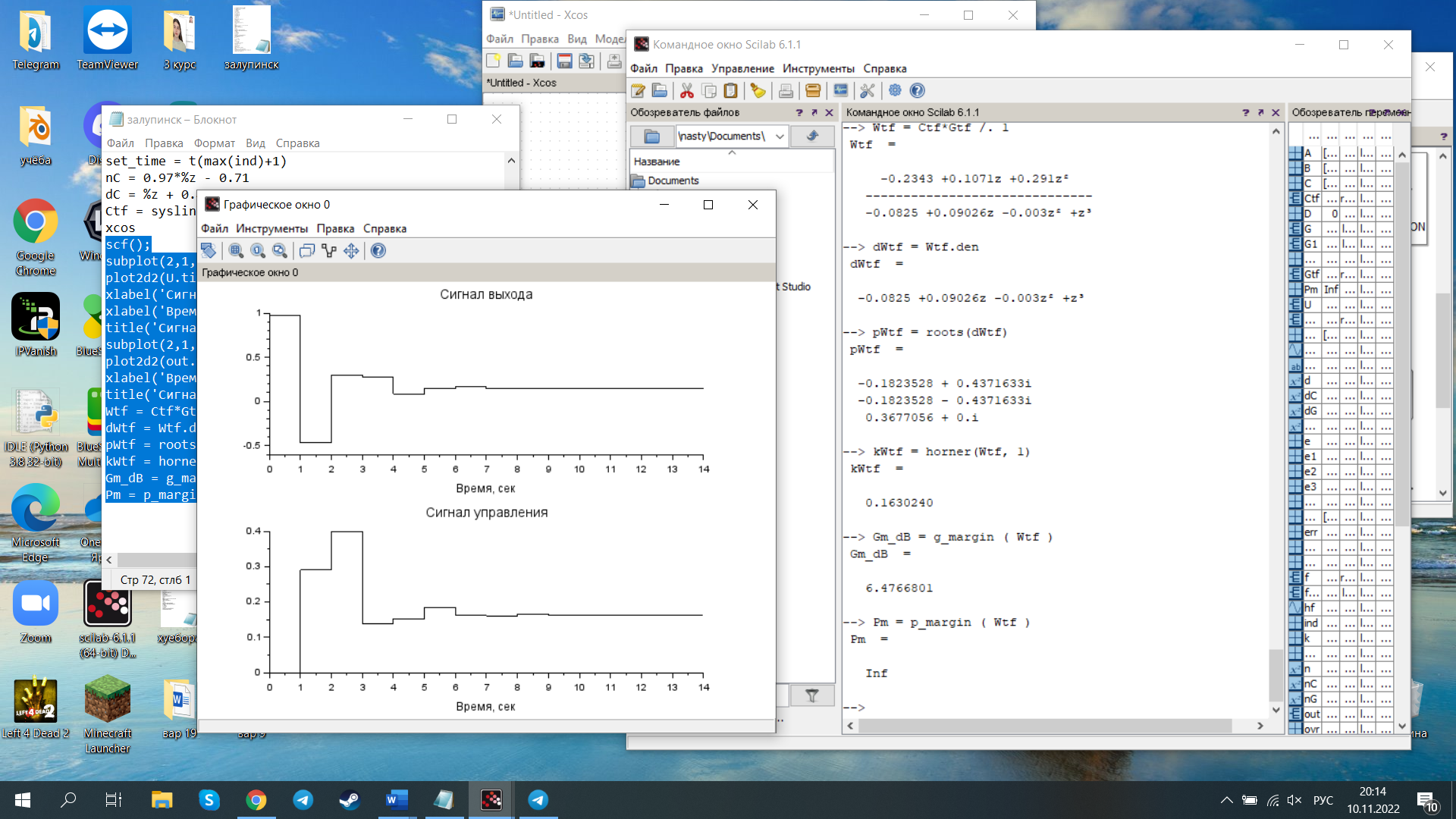



Передаточная функция разомкнутой системы: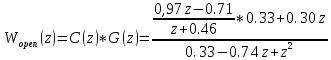




Передаточная функция замкнутой системы: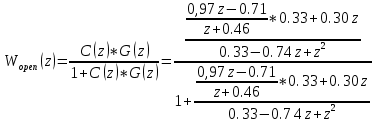



Полюса передаточной функции замкнутой системы:

p = -0.1823528 + 0.4371633i

-0.1823528 - 0.4371633i

0.3677056 + 0.i

Устойчивость: 

Система устойчива, потому что полюса меньше 1

Статический коэффициент усиления замкнутой системы:

k_W = 0.1630240

Перерегулирование:

σ = 306.1158

Время переходного процесса: 

t_п = 6

Характеристический полином замкнутой системы: 

Δ(z) = -0.0825 +0.09026z -0.003z² +z³

имеет корни

r = -0.1823528 + 0.4371633i

-0.1823528 - 0.4371633i

0.3677056 + 0.i

Устойчивость: 

Система устойчива, потому что модули собственных чисел меньше 1.

Запас устойчивости по амплитуде: 

g_m = 6.4766801

Запас устойчивости по фазе: 

ϕ_m =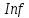

Контрольные вопросы к защите

1. 
   Как построить передаточную функцию по разностному уравнению?
   

Вернёмся снова к уравнению фильтра:

v[k] = a₂·e[k] + a₁·e[k–1] + a₀·e[k–2] – b₁·v[k–1] – b₀·v[k–2]

и запишем его в операторной форме, используя оператор запаздывания z^–1, такой что 

z^–1v[k] = v[k–1], … z^–mv[k] = v[k–m].

Получаем

v[k] = a₂·e[k] + a₁·z^–1e[k] + a₀· z^–2e[k] – b₁· z^–1v[k] – b₀· z^–2v[k]

Перенесем все значения выходного сигнала в левую часть:

v[k] + b₁· z^–1v[k] + b₀· z^–2v[k] = a₂·e[k] + a₁·z^–1e[k] + a₀· z^–2e[k]

и вынесем общие множители в обеих частях:

(1 + b₁· z^–1 + b₀· z^–2) v[k] = (a₂ + a₁·z^–1 + a₀· z^–2) e[k]

Разделим обе части равенства на скобку в левой части:

.

Умножим числитель и знаменатель на z²:



Функция



называется передаточной функцией цифрового фильтра.

2. 
   Как найти реакцию системы на известный входной сигнал по разностному уравнению?
   

Линейной называется система, которая обладает двумя свойствами:

1. 
   свойство суперпозиции: реакция на сумму сигналов равна сумме реакций этой системы на отдельные сигналы. Если {v₁[k]} – это реакция системы на входной сигнал {e₁[k]} и {v₂[k]} – это реакция системы на входной сигнал {e₂[k]}, то выход линейной системы при входе {e₁[k]+ e₂[k]} равен {v₁[k]+ v₂[k]}.
   
2. 
   свойство однородности: умножение входного сигнала на постоянную приводит к умножению выходного сигнала на ту же постоянную. Если {v₀[k]} – это реакция системы на входной сигнал {e₀[k]}, то выход линейной системы при входе {α⋅e₀[k]} равен {α⋅v₀[k]}.
   

Обычно рассматривают стационарные системы, свойства которых не изменяются во времени. Это означает, что сдвиг во времени входного сигнала на m тактов приводит к такому же сдвигу выходного сигнала. Например, если {v₀[k]} – это реакция системы на входной сигнал {e₀[k]}, то выход линейной системы при входе {e₀[k–m]} равен {v₀[k–m]}.

3. 
   Как найти z-преобразование сигнала, заданного своими значениями для k = 0, 1, 2, …?
   

Зная z-преобразование входного сигнала E(z) и передаточную функцию дискретной системы F(z), можно найти z-преобразование выходного сигнала V(z) простым умножением:

V(z) = F(z) · E(z)

Например, пусть на вход системы с передаточной функцией



действует единичный ступенчатый входной сигнал, который имеет z-преобразование 

.

Тогда

.

По теореме о начальном значении для такого изображения имеем

.

В то же время по теореме о конечном значении

.

Дискретная система может быть описана не только передаточной функцией, но и моделью в пространстве состояний:



Здесь 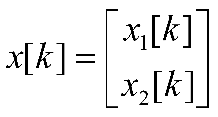– вектор состояния системы: столбец величин, которые описывают состояние системы (например, это могут быть угловая скорость и угол рыскания судна). Если вектор состояния состоит из двух компонент, его можно записать так:

.

4. 
   Как формулируется свойство суперпозиции? Как его проверить экспериментально?
   

реакция на сумму сигналов равна сумме реакций этой системы на отдельные сигналы. Если {v₁[k]} – это реакция системы на входной сигнал {e₁[k]} и {v₂[k]} – это реакция системы на входной сигнал {e₂[k]}, то выход линейной системы при входе {e₁[k]+ e₂[k]} равен {v₁[k]+ v₂[k]}.

5. 
   Как формулируется свойство однородности? Как его проверить экспериментально?
   

 умножение входного сигнала на постоянную приводит к умножению выходного сигнала на ту же постоянную. Если {v₀[k]} – это реакция системы на входной сигнал {e₀[k]}, то выход линейной системы при входе {α⋅e₀[k]} равен {α⋅v₀[k]}.

6. 
   Как изменять стиль линии при вызове функции plot?
   

строка, определяющая стиль линии. Это свойство связано со свойством объекта line_style ("стиль линии") 

7. 
   Как найти z-преобразование запаздывающего сигнала x[k–m], если известно z-преобразование X(z) исходного сигнала x[k]?
   

По теореме о начальном значении для такого изображения имеем

.

В то же время по теореме о конечном значении

.

Дискретная система может быть описана не только передаточной функцией, но и моделью в пространстве состояний:



Здесь 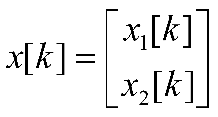– вектор состояния системы: столбец величин, которые описывают состояние системы (например, это могут быть угловая скорость и угол рыскания судна). Если вектор состояния состоит из двух компонент, его можно записать так:

.

8. 
   Что такое стационарность системы? Как проверить это свойство экспериментально?
   

Стационарность. Стационарная система обладает следующим свойством: если реакция на входной сигнал x ( t ) равна y ( t )  R [ x ( t ) ] , то для любого вещественного постоянного значения t имеем y (t  t)  R [ x (t  t)] . Это означает, что данное воздействие будет всегда приводить к одной и той же реакции независимо от времени приложения воздействия.

Система называется стационарной (инвариантной во времени), если ее параметры не изменяются во времени.

9. 
   Как построить матрицы модели в пространстве состояний по системе разностных уравнений первого порядка?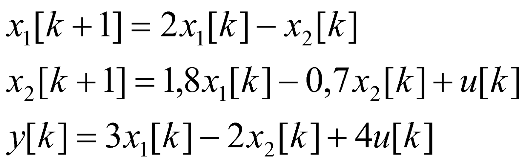
   

Устойчива ли такая система? Почему вы так решили?

10. 
    Как связаны собственные числа матрицы A модели в пространстве состояний и устойчивость системы?
    

Необходимым и достаточным условием устойчивости системы является отрицательность вещественных частей собственных чисел l_i матрицы А

Для того чтобы оценить расположение спектра матрицы A относительно мнимой оси, необходимо раскрыть характеристический определитель çA-lEç и получить характеристическое уравнение n-ой степени относительно l

çA-lEç= a₀lⁿ +a₁l^n-1 + a₂l^n-2 +...+ a_n-1l +a_n = 0.

10. 
    Постройте любую квадратную матрицу, собственные числа которой равны и , причем все её коэффициенты должны быть ненулевые.
    

10. 
    Как определить порядок системы по модели в пространстве состояний?
    

Уравнение для случая линейной непрерывной системы можно свести к следующим стандартным уравнением состояния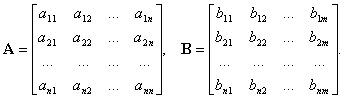



 — матрицы параметров, включающие в себя параметры системы, размерность которых соответственно  ,

10. 
    Какие функции Scilab позволяют перейти от модели в пространстве состояний к передаточной функции и обратно?
    

Функция перехода от модели в пространстве состояний (G) к передаточной функции (Gtf):

--> Gtf = ss2tf ( G )

Функция tf2ss выполняет обратный переход, от передаточной функции к модели в пространстве состояний.

--> G1 = tf2ss ( Gtf )

10. 
    Почему при переходе из пространства состояний к передаточной функции и обратно может получиться совсем другая модель?
    

Это связано с тем, что одной и той же системе соответствует бесконечное множество моделей в пространстве состояний.

10. 
    Как в Scilab выделить числитель и знаменатель передаточной функции?
    

Числитель: f.num

Знаменатель: f.den

f – передаточная функция

10. 
    Как выбирается период срабатывания таймера при моделировании дискретных систем в Scilab?
    

Period =1

10. 
    Как выбирается размер буфера блока To workspace при моделировании дискретных систем в Scilab?
    

Ставим 15 в размере буфера(моделируем 15 периодов)

10. 
    Что такое статический коэффициент усиления системы? Как его определить по передаточной функции непрерывной системы? дискретной системы?
    

Одна из важнейших характеристик линейной системы – коэффициент усиления в установившемся режиме или статический коэффициент усилении(static gain , DC - gain). Его можно определить как установившееся значение сигнала выхода при постоянном входном сигнале, равном единице. Размерность этой величины равна отношению размерностей сигналов выхода и выхода.

Статический коэффициент усиления системы можно найти по теореме о конечном значении:

.

10. 
    Как связан статический коэффициент усиления системы и установившийся сигнал при постоянном входном воздействии?
    

Статический коэффициент усиления системы можно определить как установившееся значение сигнала выхода при постоянном входном сигнале, равном единице.

10. 
    Что такое перерегулирование? Как его найти, если установившееся значение отрицательное?
    

Перерегулирование —ограниченный по времени выброс сигнала или функции над целевым значением. 

Если установившееся значение отрицательное, при вычислении перерегулирования нужно выполнить «зеркальное отражение» сигналов – поменять знаки у и . В формуле вместо максимального значения нужно взять минимальное:

.

10. 
    Как определяется время переходного процесса?
    

Время переходного процесса – это время, после которого сигнал выхода отличается от установившегося  значения не более, чем на заданную малую величину (обычно 2% или 5% от установившегося значения).

err = abs(yStep-yInf)

ind = find(err >= 0.05*yInf)

set_time = t(max(ind)+1)

10. 
    Известен характеристический полином замкнутой системы. Как определить, устойчива ли система?
    

Если модули собственных чисел меньше 1, то система устойчива

23. 
    Как найти передаточную функцию разомкнутой системы? замкнутой системы?
    

Если разорвать обратную связь, то получается разомкнутая система.

Её передаточная функция равна произведению передаточных функций двух блоков:

W_open(z) = C(z) G(z).

Для замкнутой системы справедлива такая же формула, как и для непрерывных систем:

.

24.Что такое нули и полюса передаточной функции? На что они влияют?

Передаточные функции содержат особые точки на комплексной плоскости -нули и полюса. Полюса - это те значения S, при которых передаточная функция превращается в бесконечность. Для определения полюсов необходимо собственный оператор (знаменатель передаточной функции) приравнять к нулю и произвести решение алгебраического уравнения относительно S. Нули - это те значения S, при которых передаточная функция равна нулю.

25.Известна передаточная функция замкнутой системы. Как определить, устойчива ли система?

Если модули собственных чисел меньше 1, то система устойчива

26.Что такое запас устойчивости по амплитуде? по фазе? В каких единицах измеряются запасы устойчивости?

Запас устойчивости по амплитуде h – это минимальный отрезок, характеризующий расстояние между критической точкой и ближайшей точкой пересечения годографом Найквиста вещественной оси на отрезке [0, -1]

Запас устойчивости по фазе g - это минимальный угол, образуемый радиусом, проходящим через точку пересечения годографа Найквиста с окружностью единичного радиуса с центром в начале координат и отрицательной вещественной полуосью.